
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Стационарное и нестационарное уравнение Шредингера
|
|
|
|
Плоская волна де Бройля
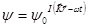 (3.10)
(3.10)
соответствует свободному и равновесному движению частицы в определенном направлении и с определенным импульсом. Но частица, даже в свободном пространстве и, в особенности, в силовых полях может совершать и другие движения, описываемые более сложными волновыми функциями. Основная задача волновой механики как раз и состоит в нахождении волновых функций. Для ее решения служит волновое уравнение, найденное Шредингером в 1926 г. Это- основное уравнение квантовой механики, но оно справедливо только в нерелятивистском случае, то есть в случае движений, меньших скорости света в вакууме.
Уравнение должно быть общим уравнением, то есть должно быть пригодно для решения всех, а не только частных задач. Поэтому в него не должны входить значения параметров. Кроме того, это уравнение должно быть линейно и однородно по ψ.
Одним из решений его в свободном пространстве должна быть плоская волна де Бройля. Найдем дифференциальное уравнение, удовлетворяющее перечисленным выше условиям. Дифференцирование (3.10) по х дает
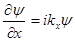 ;
; 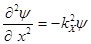 .
.
В общем случае
 . (4.7)
. (4.7)
Продифференцируем теперь (3.10) по времени
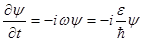 . (4.8)
. (4.8)
Разделим (4.7) на (4.8) и учтем, что  . Таким путем придем к однородному линейному уравнению
. Таким путем придем к однородному линейному уравнению
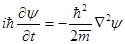 , (4.9)
, (4.9)
которое справедливо для любых движений частицы в свободном пространстве. Это есть уравнение Шредингера в отсутствие силовых полей.
Обобщим теперь уравнение (4.9) на случай движения силовых полей, характеризующихся потенциальной энергией U 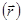 :
:
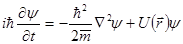 . (4.10)
. (4.10)
Это есть временное или общее уравнение Шредингера.
Особое значение в квантовой механике имеет стационарное состояние. Это такие состояния, в которых все наблюдаемые физические параметры не меняются с течением времени. Сама волновая функция ψ не относится к этим параметрам. Она принципиально не наблюдаема. Для стационарных состояний
|
|
|
 . (4.11)
. (4.11)
Для определения функции 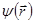 в стационарных состояниях подставляем (4.11) в (4.10) и находим
в стационарных состояниях подставляем (4.11) в (4.10) и находим
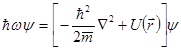 .
.
По аналогии со световыми квантами примем, что  представляет собой полную энергию частицы в стационарном состоянии. Получим:
представляет собой полную энергию частицы в стационарном состоянии. Получим:
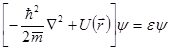 . (4.12)
. (4.12)
Это уравнение не содержит времени и называется уравнением Шредингера для стационарных состояний или стационарным уравнением Шредингера.
Квантование энергии возникает потому, что на волновые функции, являющиеся решением уравнения Шредингера (4.12), накладываются определенные естественные ограничения. При этих ограничениях уравнение (4.12) имеет решение не при всех, а только при избранных значениях параметра  .
.
Естественные ограничения, накладываемые на решение уравнения Шредингера, состоят в том, что волновая функция 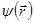 и ее первые пространственные производные должны быть конечны, однозначны и непрерывны даже в точках разрыва потенциальной функции
и ее первые пространственные производные должны быть конечны, однозначны и непрерывны даже в точках разрыва потенциальной функции 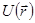 . (Однозначность означает, что при обходе по любому замкнутому контуру функция
. (Однозначность означает, что при обходе по любому замкнутому контуру функция 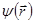 должна возвращаться к своему исходному значению). Избранные значения параметра
должна возвращаться к своему исходному значению). Избранные значения параметра  , для которых уравнение (4.12) имеет решения, удовлетворяющие перечисленным ограничениям, называются собственными значениями величины
, для которых уравнение (4.12) имеет решения, удовлетворяющие перечисленным ограничениям, называются собственными значениями величины  для уравнения (4.12), а соответствующие им решения - собственными функциями того же уравнения.
для уравнения (4.12), а соответствующие им решения - собственными функциями того же уравнения.
Собственные значения  и принимаются за возможные значения энергии в стационарных состояниях. Собственные значения энергии
и принимаются за возможные значения энергии в стационарных состояниях. Собственные значения энергии  могут быть дискретными, а могут быть и непрерывными. В первом случае говорят, что энергетический спектр дискретный, а во втором - непрерывный.
могут быть дискретными, а могут быть и непрерывными. В первом случае говорят, что энергетический спектр дискретный, а во втором - непрерывный.
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 8708; Нарушение авторских прав?; Мы поможем в написании вашей работы!