Разложение определителя по строке

Основные свойства определителей.

Свойство 1. Определитель не изменяется при транспонировании, т.е.

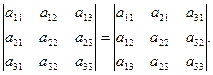
Свойство 2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.

.

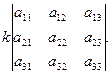Свойство 3. Определитель, две строки которого пропорциональны, равен 0.

Свойство 4. При перестановке двух строк определителя он умножается на –1.

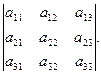
Свойство 5. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

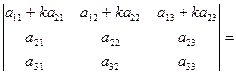
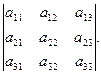
Определение Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит выбранный элемент.

Обозначение: выбранный элемент определителя, его минор.

Определение Алгебраическим дополнением элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е.

Теорема Определитель равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения, т.е.

где i=1,2,3.

Замечание 1. Свойства определителей 3-го порядка справедливы и для определителей n-го порядка.

Замечание 2. На практике определители высоких порядков вычисляют с помощью разложения по строке или столбцу. Это позволяет понизить порядок вычисляемых определителей и в конечном счете свести задачу к нахождению определителей 3-го порядка.

4. Определение. Матрицей размера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются a_ij, где i- номер строки, а j- номер столбца. А =

Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

// Определение. Матрица вида: = E, называется единичной матрицей.

Определение. Если a_mn = a_nm, то матрица называется симметрической .Пример. - симметрическая матрица

Определение.

Квадратная матрица вида называется диагональной матрицей.

Определение. Матрицу В называют транспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В. А = ; В = А^Т= ; другими словами, b_ji = a_ij. Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера.

Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц. c_ij = a_ij ± b_ij С = А + В = В + А. Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

Операция умножения матриц.

Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам: A×B = C; . Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

Определение. Элементарными преобразованиями матрицы назовем следующие преобразования:

1) умножение строки на число, отличное от нуля;

2) прибавление к одной строке другой строки;

3) перестановка строк;

4) вычеркивание (удаление) одной из одинаковых строк (столбцов);

5) транспонирование; Те же операции, применяемые для столбцов, также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк (столбцов).

Определение Определитель, составленный из элементов квадратной матрицы А, называется определителем матрицы и обозначается D(А) или det (A).

5. Определение Квадратная матрица А называется вырожденной, если , и невырожденной, если .

Определение Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е. При этом В обозначается .

Теорема. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной.

Обратная матрица вычисляется по формуле

А^-1 = 1/D ,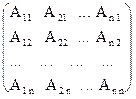

где А _{i j} - алгебраические дополнения элементов a _{i j}.

Определение Ранг матрицы – это порядок ее наибольшего ненулевого минора.

Обозначения: r(A), R(A), Rang A.

Примеры:

1. , r(A)=0.

2. . Матрица В содержит единственный ненулевой элемент - являющийся минором 1-го порядка. Все определители более высоких порядков, составленные из элементов этой матрицы, будут содержать 0-ю строку и поэтому равны 0. Следовательно, r(B)=1.

3. . Единственным минором 3-го порядка является определитель матрицы С, но он равен 0, поскольку содержит пропорциональные столбцы. Следовательно, r(C)<3.

Для того, чтобы доказать, что r(C)=2, достаточно указать хотя бы один минор 2-го порядка, не равный 0, например, Значит, r(C)=2.

4. следовательно, r(E)=3.

Замечание. Для матриц большой размерности непосредственное вычисление всех миноров затруднительно. Поэтому в этом случае можно преобразовать матрицу к так называемому треугольному виду (когда элементы, стоящие ниже 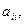равны 0), воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями).

Пример. Найдем ранг матрицы . Теоретически ранг этой матрицы может принимать значения от 1 до 4, так как из элементов матрицы можно создать миноры по 4-й порядок включительно. Но вместо того, чтобы вычислять все возможные миноры 4-го, 3-го и т.д. порядка, применим к матрице А эквивалентные преобразования. Вначале добьемся того, чтобы в первом столбце все элементы, кроме первого, равнялись 0. Для этого запишем вместо второй строки ее сумму с первой, а вместо третьей – разность третьей и удвоенной первой:

.

Затем из третьей строки вычтем вторую, а к четвертой прибавим вторую:

.

После вычеркивания нулевых строк получим матрицу размерности для которой максимальный порядок миноров, а, следовательно, и максимально возможное значение ранга равно 2:

.

Ее минор следовательно,

Контрольные вопросы:

1. Определитель второго порядка и его свойства

2. Определитель третьего порядка

2. Определители п-го порядка

3. Миноры и алгебраические дополнения

4. Матрицы. Действия над матрицами

5. Обратная матрица, вычисление и ранг матрицы

Литература: [3, с. 23,70,95],[8, с.40-65]

Лекция № 2. Тема: Системы линейных уравнений. Однородные и неоднородные уравнения. Теорема Кронекера- Капелли. Методы решения систем линейных уравнений: метод Крамера, метод Гаусса, метод матричного исчисления.

Цель: Рассмотреть условие совместности системы уравнений, виды систем, матричную форму записи. Рассмотреть различные методы решения систем линейных уравнений.

План:

1. Системы линейных уравнений. Однородные и неоднородные уравнения.

2. Теорема Кронекера- Капелли.

3. Метод Крамера

4. Метод матричного исчисления.

5. Метод Гаусса

1. Определение Линейным уравнением называется уравнение вида

где и b – числа, - неизвестные.

Определение Системой линейных уравнений (линейной системой) называется система вида

(1)

где 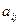, - числа, - неизвестные, n – число неизвестных, m – число уравнений.

Определение. Решением линейной системы (1) называется набор чисел

которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.

Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.

//

Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.

Определение. Если b₁, b₂, …,b_m = 0, то система называется однородной. Однородная система всегда совместна.

Определение. Для системы линейных уравнений вида (1) матрица А = называется матрицей системы, а матрица А^*= называется расширенной матрицей системы.

B = - матрица свободных членов, X = _- матрица неизвестных. Систему уравнений можно записать:

A×X = B. (матричная запись системы)

Систему однородных уравнений можно записать в виде:A×X = 0

2. Теорема Кронекера – Капелли. (условие совместности системы) Система(1) совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

Теорема Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.

Теорема Для того, чтобы система однородных уравнений имела ненулевое решение, необходимо и достаточно чтобы ранг ее основной матрицы был меньше числа п неизвестных.

Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений.

3. Теорема. (Правило Крамера): Система из n уравнений с n неизвестными в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам: x_i = D_i/D, где D = det A, а D_i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i. D_i =

Правило Крамера позволяет найти единственное решение системы или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:

1) Если 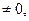система (2.3) имеет единственное решение, определяемое по формулам: .

2) Если = =0, система имеет бесконечно много решений.

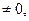3) Если =0, а хотя бы один из система не имеет решений.

2. . Здесь поскольку имеет два одинаковых столбца.

Следовательно, система не имеет единственного решения. Найдем и

поэтому система имеет бесконечно много решений.

3. . Для этой системы но

следовательно, решений нет.

4. Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных. Метод удобен для решения систем невысокого порядка. Метод основан на применении свойств умножения матриц. Пусть дана система уравнений: Составим матрицы: A = ; B = ; X = .

Тогда систему можно записать в виде матричного уравнения: АХ = В.

Пусть матрица А – невырожденная, тогда существует обратная к ней матрица

Умножим обе части последнего равенства слева на Получим

Но 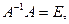тогда , а поскольку

Итак, решением матричного уравнения является произведение матрицы, обратной к А, на столбец свободных членов системы.

5. Метод Гаусса. В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных. Рассмотрим систему линейных уравнений: Разделим обе части 1–го уравнения на a₁₁ ¹ 0, затем: 1) умножим на а₂₁ и вычтем из второго уравнения 2) умножим на а₃₁ и вычтем из третьего уравнения и т.д. Получим: , где d_1j = a_1j/a₁₁, j = 2, 3, …, n+1. d_ij = a_ij – a_i1d_1j i = 2, 3, …, n; j = 2, 3, …, n+1. Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.

Контрольные вопросы:

1 .Системы линейных уравнений. Однородные и неоднородные уравнения.

2. Теорема Кронекера- Капелли.

3. Метод Крамера

4. Метод матричного исчисления.

5. Метод Гаусса

Литература: [3, с. 77,83 ],[8, с.70-82]

Лекция № 3.Тема: Векторы. Линейные операции над векторами. Проекция вектора на ось. Декартова система координат. Скалярное произведение векторов. Векторное и смешанное произведение векторов, их основные свойства и геометрический смысл. Координатное выражение векторного и смешанного произведения.

Цель:Дать понятия вектора,координат вектора. Рассмотреть линейные действия над векторами. Дать понятие декартовой системы координат. Рассмотреть определение и основные свойства скалярного, векторного и смешанного произведения векторов

План:

1.Векторы. Линейные операции над векторами. Проекция вектора на ось

2.Декартова система координат. Скалярное произведение векторов

3.Векторное и смешанное произведения векторов

1. Определение Вектором называется направленный отрезок.

Обозначения: a, , .

Определение Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Вектор называется нулевым, если его начальная и конечная точки совпадают. Нулевой вектор не имеет определенного направления.

Определение Два вектора называются равными, если они коллинеарны, имеют одинаковую длину (модуль) и одинаковое направление.

Замечание. Таким образом, мы изучаем так называемые свободные векторы, начальная точка которых может быть выбрана произвольно. Векторы, для которых важна точка приложения, называются присоединенными (связанными) и используются в некоторых разделах физики.

Определение Векторы называются компланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях.

Дата добавления: 2014-11-09