
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Перемещения при изгибе. Метод начальных параметров
|
|
|
|
Изгиб балки сопровождается искривлением ее оси. При поперечном изгибе ось балки принимает вид кривой, расположенной в плоскости действия поперечных нагрузок. При этом точки оси получают поперечные перемещения, а поперечные сечения совершают повороты относительно своих нейтральных осей. Углы поворота поперечных сечений принимаются равными углам наклона j, касательной к изогнутой оси балки (рис. 5.23).
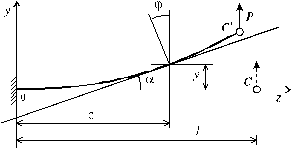 Рис. 5.23
Рис. 5.23
|
Прогибы и углы поворотов в балках являются функциями координаты z и их определение необходимо для расчета жесткости. Рассмотрим изгиб стержня в одной из главных плоскостей например, в плоскости yz. Как показывает практика, в составе реальных сооружений стержни испытывают весьма малые искривления (y max/ l = 10-2 - 10-3, где y max - максимальный прогиб; l - пролет балки).
В этом случае неизвестными функциями, определяющими положение точек поперечных сечений балки являются y (z) и j (z) = = a (z) (рис.5.23). Совокупность значений этих параметров по длине балки образуют две функции от координаты z - функцию перемещений y (z) и функцию углов поворота j (z). Из геометрических построений (рис. 5.23) наглядно видно, что угол наклона касательной к оси z и угол поворота поворота поперечных сечений при произвольном z равны между собой. В силу малости углов поворота можно записать:
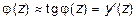 . (5.17)
. (5.17)
Из курса математического анализа известно, что кривизна плоской кривой y (z) выражается следующей формулой:
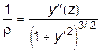 .
.
Если рассмотреть совместно соотношение (5.9) и последнее выражение, то получим нелинейное дифференциальное уравнение изогнутой оси балки, точное решение которого, как правило, затруднительно. В связи с малостью величины 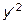 по сравнению с единицей последнее выражение можно существенно упростить, и тогда
по сравнению с единицей последнее выражение можно существенно упростить, и тогда
|
|
|
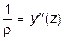 . (5.18)
. (5.18)
Учитывая (5.9), из (5.18) получим следующее важное дифференциальное соотношение
 , (5.19)
, (5.19)
где Ix - момент инерции поперечного сечния балки, относительно ее нейтральной оси; Е - модуль упругости материала; E Ix - изгибная жесткость балки.
Уравнение (5.19), строго говоря, справедливо для случая чистого изгиба балки, т.е. когда изгибающий момент Mx (z) имеет постоянное значение, а поперечная сила равна нулю. Однако это уравнение используется и в случае поперечного изгиба, что равносильно пренебрежению искривлений поперечных сечений за счет сдвигов, на основании гипотезы плоских сечений.
Введем еще одно упрощение, связанное с углом поворота поперечного сечения. Если изогнутая ось балки является достаточно пологой кривой, то углы поворота сечений с высокой степенью точности можно принимать равными первой производной от прогибов. Отсюда следует, что прогиб балки принимает экстремальные значения в тех сечениях, где поворот равен нулю.
В общем случае, для того, чтобы найти функции прогибов y (z) и углов поворота j (z), необходимо решить уравнение (5.19), с учетом граничных условий между смежными участками.
Для балки, имеющей несколько участков, определение формы упругой линии является достаточно сложной задачей. Уравнение (5.19), записанное для каждого участка, после интегрирования, содержит две произвольные постоянные.
На границах соседних участков прогибы и углы поворота являются непрерывными функциями. Данное обстоятельство позволяет определить необходимое число граничных условий для вычисления произвольных постоянных интегрирования.
Если балка имеет n - конечное число участков, из 2 n числа граничных условий получим 2 n алгебраических уравнений относительно 2 n постоянных интегрирования.
Если момент и жесткость являются непрерывными по всей длине балки функциями Mx (z) и E Ix (z), то решение может быть получено, как результат последовательного интегрирования уравнения (5.19) по всей длине балки:
|
|
|
интегрируя один раз, получаем закон изменения углов поворота
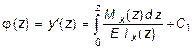 ,
,
интегрируя еще раз, получаем функцию прогибов
 .
.
Здесь C 1 и С 2 произвольные постоянные интегрирования должны быть определены из граничных условий.
Если балка имеет постоянное поперечное сечение по длине, то для определения функций прогибов и углов поворота удобно применить метод начальных параметров, суть которого в следующем.
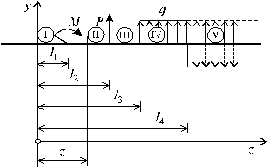 Рис. 5.24
Рис. 5.24
|
Рассмотрим балку (рис. 5.24) с постоянным поперечным сечением, нагруженную взаимоуравновешенной системой положительных силовых факторов (т.е., вызывающих вертикальные перемещения сечений балки в положительном направлении оси y). Начало системы координат поместим на левом конце балки так, чтобы ось z проходила вдоль оси балки, а ось y была бы направлена вверх. На балку действуют: момент М, сосредоточенная сила Р и равномерно распределенная на участке бруса нагрузка интенсивностью q (рис. 5.24).
Задача заключается в том, чтобы выявить особенности, вносимые в уравнение упругой линии, различными типами внешних силовых факторов. Для этого составим выражение изгибающих моментов для каждого из пяти участков заданной системы.
Участок I (0£ z £ l 1 ) Mx ( z ) = 0.
Участок II ( l 1 £ z £ l 2 ) Mx ( z ) = M.
Участок III ( l 2 £ z £ l 3 ) Mx ( z ) = M + P (z - l 2).
Участок IV ( l 3£ z £ l 4) Mx ( z ) = M + P (z - l 2) + 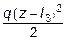 .
.
Уч-ток V( l 4 £ z £ l 5) Mx ( z ) = M + P (z - l 2) +  .
.
На участке V, где распределенная нагрузка отсутствует, при выводе выражения для изгибающего момента, с целью сохранения рекуррентности формул для разных участков была приложена взаимоуравновешенная распределенная нагрузка.
Для вывода обобщенного выражения изгибающего момента введем следующий оператор 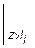 , означающий, что члены выражения, стоящее перед ним следует учитывать при z > li и игнорировать при z £ li. На основании этого, обобщенное выражение момента Mx (z) для произвольного сечения z может быть записано единой формулой:
, означающий, что члены выражения, стоящее перед ним следует учитывать при z > li и игнорировать при z £ li. На основании этого, обобщенное выражение момента Mx (z) для произвольного сечения z может быть записано единой формулой:
Mx (z) = M 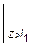 + P (z - l 2)
+ P (z - l 2) 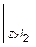 +
+ 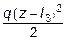
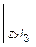 -
-
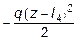
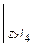 . (5.20)
. (5.20)
Подставляя (5.20) в (5.19) и дважды интегрируя, получим выражение для прогибов:
E Ix y (z) = C 0 + C 1 z + 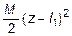
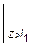 +
+ 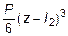
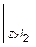
+ 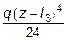
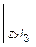 -
- 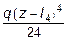
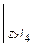 . (5.21)
. (5.21)
|
|
|
Постоянные интегрирования C 0 и C 1 по своей сути означают:
C 0 = E Ix y (0), C 1 = 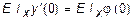 (5.22)
(5.22)
и определяются из граничных условий на левом конце балки. Тогда формула для прогибов примет следующий окончательный вид:
E Ix y (z) = E Ix y 0 + 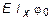 z +
z + 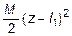
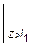 +
+ 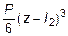
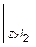 +
+
+ 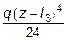
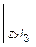 -
- 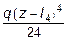
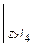 . (5.23)
. (5.23)
Соответственно, формула для углов поворотов сечений балки определяется из (5.23) простым дифференцированием:
E Ix j (z) = 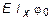 +
+ 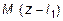
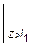 +
+ 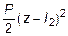
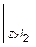
+ 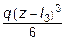
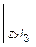 -
- 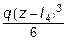
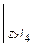 . (5.24)
. (5.24)
Как видно, для определения прогибов и углов поворота балок данным методом начальных параметров достаточно знание лишь значений прогиба y 0 , угла поворота j0 в начале системы координат, т.е. так называемых начальных параметров. Поэтому данный метод и называется методом начальных параметров.
|
|
|
|
|
Дата добавления: 2015-06-30; Просмотров: 307; Нарушение авторских прав?; Мы поможем в написании вашей работы!