
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Означення диференціального рівняння і розв’язку
|
|
|
|
Варианты контрольной работы
Решение
Пример 8
Решение
Пример 7
Решение
Пример 6
Решение
Пример 5
Решение
Пример 4
Решение
Пример 3
Решение
Пример 2
Решение
Пример 1
Решить уравнение 
Данное уравнение является уравнением в полных дифференциалах, т. к.  , где M =2 x + y 2, N =2 xy ‑2 y по условию. Согласно определению уравнения в полных дифференциалах решение сводится к нахождению функции u (x, y), полный дифференциал которой равен левой части уравнения
, где M =2 x + y 2, N =2 xy ‑2 y по условию. Согласно определению уравнения в полных дифференциалах решение сводится к нахождению функции u (x, y), полный дифференциал которой равен левой части уравнения
 . (7)
. (7)
Интегрируем равенство  по переменной x, получим
по переменной x, получим
 . (8)
. (8)
Для нахождения φ (y) дифференцируем равенство (8) по переменной y,имеем  . С другой стороны, в силу (7),
. С другой стороны, в силу (7),  . Приравнивая правые части последних выражений, находим φ /(y):
. Приравнивая правые части последних выражений, находим φ /(y):
2 xy + φ /(y) = 2 xy ‑ 2 y  φ /(y)= ‑2 y
φ /(y)= ‑2 y  φ (y) = ‑ y 2+ C.
φ (y) = ‑ y 2+ C.
Полученное значение φ (y) записываем в выражение (8) и получаем общее решение данного дифференциального уравнения
x 2 + xy 2 – y 2 = C.
Решить уравнение 
В данном уравнении M = 2 xy, N = – (2 x 2+3 y). Условие (2) не вы-
полнено, так как
 .
.
Поэтому исходное уравнение не является уравнением в полных дифференциалах и для его решения необходимо найти интегрирующий множитель, для определения вида которого используем функцию ψ (ω) (см случай I):
 .
.
При ω = y получим  . Отсюда, интегрирующий множитель имеет следующий вид:
. Отсюда, интегрирующий множитель имеет следующий вид:
 .
.
Умножим исходное уравнение на интегрирующий множитель  , получим уравнение в полных дифференциалах
, получим уравнение в полных дифференциалах
 , (9)
, (9)
которое решаем аналогично примеру 1.
1) согласно определению полного дифференциала записываем
 ,
,
2) интегрируем по переменной x
 ,
,
3) полученное равенство дифференцируем и приравниваем к N (x, y)
|
|
|
 ,
, 

4) из последнего выражения получаем, что
 .
.
Учитывая значение  , записываем общее решение дифференциального уравнения в следующем виде:
, записываем общее решение дифференциального уравнения в следующем виде:
 .
.
Решить уравнение 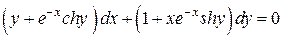
Аналогично решению в предыдущих примерах проверим выполнения условия (2):
 ,
,
где M =  , N =
, N =  .
.
Найдем интегрирующий множитель согласно формуле (6), получим
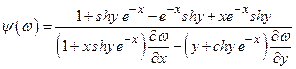 . Тогда
. Тогда  при ω = x.
при ω = x.
В силу I интегрирующий множитель 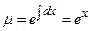 . Далее решаем уравнение аналогично вышерассмотренным примерам.
. Далее решаем уравнение аналогично вышерассмотренным примерам.
1) умножаем искомое уравнение на интегрирующий множитель
 ,
,
2) согласно определению полного дифференциала записываем
 ,
,
3) интегрируем по переменной x
 ,
,
4) полученное равенство дифференцируем и приравниваем к N (x, y)
 ,
,
5) из последнего выражения получаем, что  .
.
Учитывая значение  , записываем общее решение дифференциального уравнения в следующем виде:
, записываем общее решение дифференциального уравнения в следующем виде:
 .
.
Решить уравнение 
Проверим условие (2) и в случае его не выполнения, найдем интегрирующий множитель выше представленным методом:
 ,
,
где M = x, N =  . Отсюда,
. Отсюда,  . Отметим, что при
. Отметим, что при 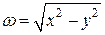 , имеем
, имеем  и
и  , тогда
, тогда  принимает следующий вид:
принимает следующий вид:  . Таким образом, получили, что
. Таким образом, получили, что  , если
, если 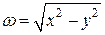 . Найдем интегрирующий множитель
. Найдем интегрирующий множитель 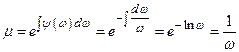 , т.е.
, т.е.  .
.
Далее решаем уравнение аналогично примеру 3:
1) умножаем искомое уравнение на интегрирующий множитель
 ,
,
2) согласно определению полного дифференциала записываем
 ,
,
3) интегрируем по переменной x
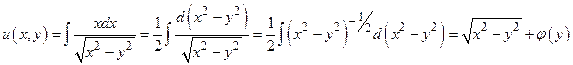
4) полученное равенство дифференцируем и приравниваем к N (x, y)
 ,
,
5) из последнего выражения получаем, что
 .
.
Записываем значение  в функцию
в функцию  (см п.3 данного примера), получаем общее решение дифференциального уравнения в следующем виде:
(см п.3 данного примера), получаем общее решение дифференциального уравнения в следующем виде:
 .
.
Решить уравнение 
В искомом уравнении не выполняется условие (2):
 , т. к.
, т. к.  , где по условию М = y + 4 x 3cos2 xy, N = x.
, где по условию М = y + 4 x 3cos2 xy, N = x.
Для нахождения интегрирующего множителя, определим функцию ψ (ω) аналогично вышерассмотренным примерам:
|
|
|
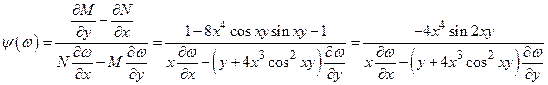 .
.
Здесь, если взять  , то
, то  ,
,  .
.
Тогда искомая функция ψ (ω) имеет следующий вид:

Следовательно,  , если
, если  . Отсюда, интегрирующий
. Отсюда, интегрирующий
множитель 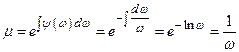 , т.е.
, т.е.  .
.
Далее решаем уравнение аналогично примеру 3:
1) умножаем искомое уравнение на интегрирующий множитель
 ,
,
2) согласно определению полного дифференциала записываем
 ,
,
3) интегрируем по переменной x

4) полученное равенство дифференцируем и приравниваем к N (x, y)
 ,
,
5) из последнего выражения получаем, что  .
.
Записываем значение  в функцию
в функцию  (см п.3 данного примера), получаем общее решение дифференциального уравнения в следующем виде:
(см п.3 данного примера), получаем общее решение дифференциального уравнения в следующем виде:
 .
.
Решить уравнение 
Данное уравнение не является уравнением в полных дифференциалах (см пример 1, 2). Найдем интегрирующий множитель:

При  функция
функция  примет вид
примет вид


 .
.
Тогда интегрирующий множитель
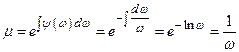 , т.е.
, т.е.  .
.
Уравнение, полученное после умножения исходного на интегрирующий множитель, является уравнением в полных дифференциалах следующего вида:
 .
.
Тогда



 .
.
Таким образом,  и общее решение искомого уравнения получаем в виде
и общее решение искомого уравнения получаем в виде  .
.
Решить уравнение 
Данное уравнение не является уравнением в полных дифференциалах (см пример 1, 2). Найдем интегрирующий множитель:
 , тогда при
, тогда при 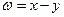 функция
функция  примет вид
примет вид  , т.е.
, т.е.  . Тогда интегрирующий множитель
. Тогда интегрирующий множитель  .
.
Полученное уравнение в полных дифференциалах
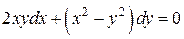
решаем аналогично предыдущим примерам:
 ,
,
 .
.
Получаем общее решение  .
.
Решить уравнение 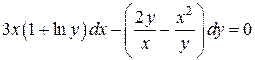
Так как данное уравнение не является уравнением в полных дифференциалах, то в начале решения найдем интегрирующий множитель:
 .
.
Если  , то функция
, то функция 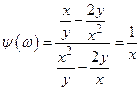 , т.е.
, т.е.  . Тогда интегрирующий множитель
. Тогда интегрирующий множитель  .
.
После умножения на полученный интегрирующий множитель данное уравнение является уравнением в полных дифференциалах следующего вида:
 ,
,
 ,
,
 ,
,  .
.
Таким образом, общее решение данного уравнения получаем в следующем виде:
 .
.
В ниже приведенных вариантах необходимо выбратьинтегрирующий множитель μ (x), μ (y), μ (xy), μ (x 2 +y 2), μ (x 2 ‑ y 2), μ (x ± y) и решить предложенные дифференциальные уравнения:
Вариант 1
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
Вариант 2
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
Вариант 3
|
|
|
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
Вариант 4
1. 
2. 
3. 
4. 
5. 
6. 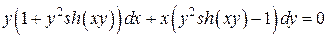
7. 
8. 
9. 
10. 
Вариант 5
1. 
2. 
3. 
4. 
5. 
6. 
7. 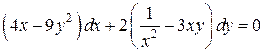
8. 
9. 
10. 
Вариант 6
1. 
2. 
3. 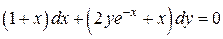
4. 
5. 
6. 
7. 
8. 
9. 
10. 
Вариант 7
1. 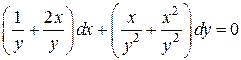
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 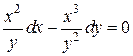
10. 
Вариант 8
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
Вариант 9
1. 
2. 
3. 
4. 
5. 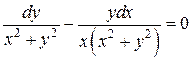
6. 
7. 
8. 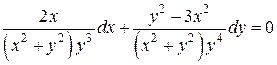
9. 
10. 
Вариант 10
1. 
2. 
3. 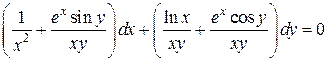
4. 
5. 
6. 
7. 
8. 
9. 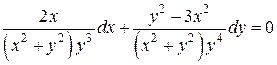
10. 
Литература
1. Богданов, Ю.С. Дифференциальные уравнения / Ю.С. Богданов, Ю.Б. Сыроид ‑ Минск: Выш. школа, 1983. – 240 с.
2. Матвеев, Н.М. Сборник задач и упражнений по обыкновенным дифференциальным уравнениям / Н.М. Матвеев – Минск: Выш. школа, 1974. – 414 с.
3. Матвеев, Н.М. Методы интегрирования обыкновенных дифференциальных уравнений / Н.М. Матвеев – Минск: Выш. школа, 1974. – 766 с.
4. Эльсгольц, Л.С. Дифференциальные уравнения и вариационное исчисление / Л.С. Эльсгольц ‑ Москва: Наука, 1969. – 424 с.
5. Филиппов, А.Ф. Сборник задач по дифференциальным уравнениям / А.Ф. Филиппов ‑ Москва: Наука, 1979. – 128 с.
Означення. Вираз виду F( ,
, 
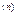 )=0 де
)=0 де  – незалежна змінна, а
– незалежна змінна, а  – незалежна функція від цієї змінної,
– незалежна функція від цієї змінної, 
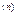 - похідні цієї функції, називається диференціальним рівнянняму звичайних похідних.
- похідні цієї функції, називається диференціальним рівнянняму звичайних похідних.
По порядку найвищої похідної визначається порядок рівняння.
Означення. Функція 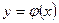 визначена на довільній множині, називається рішенням рівняння на даній множині, якщо при підстановці функції в рівняння воно звертається у вірну тотожність.
визначена на довільній множині, називається рішенням рівняння на даній множині, якщо при підстановці функції в рівняння воно звертається у вірну тотожність.
Приклад. y′=  y=kx, k=const
y=kx, k=const
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 259; Нарушение авторских прав?; Мы поможем в написании вашей работы!