Поверхностные интегралы 1 рода

Определения. Поверхность наз. гл., если в " ее точке $ касательная плоскость, и она плавно меняется при переходе в другую точку. Поверхность задают с помощью уравнений и наиболее удобными являются параметрические, они имеют вид 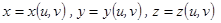и выражают координаты точки поверхности через параметры 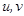. Для гл. поверхности необходимо, чтобы эти уравнения подчинялись опред. условиям. Их можно выразить через частные производные от радиуса вектора точки.

Множество 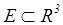наз. элем гл. поверхн., если его можно задать уравн. 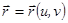, , 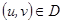где 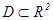– допуст. множ., при этом функция 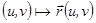удовлетворяет условиям:

1) 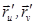непр., 2) 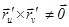, 3) правило 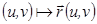действует вз-одн.

Условие 1) означает, что можно провести касат. к изолиниям и они непр. меняются, 2) означает, что касат. векторы 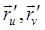лин. незав. и образуют касат. пл., 3) позволяет считать пару 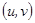координатами точки поверхн.

Площадь ЭГП выражается по опред. интегралом 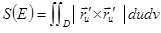. Такой вид площадь приобретает в результате следующих рассмотрений. Пусть D прямоуг., разобьем его на частичные прямоуг., берем один из них, его образ на E – криволин четырехугольник, стороны его приблизительно = 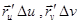, а пл. = длине 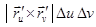, сумма всех таких порций образует интегральную сумму указанного двойного инт. Можно показать, что инт. не зависит от регулярной параметризации поверхн. Выражение 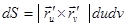наз. элем площади.

Пусть f огранич на гл. поверхн. 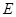, 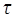- разбиение 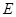на n частей, площади и диаметры которых = 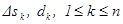, в каждой части выберем т. 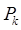и образуем инт. сумму 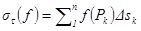. Введем ранг: 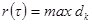и опр. предел сумм: 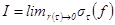если 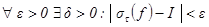как только 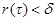незав. от выбора .

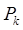Поверхностным интегралом наз. число 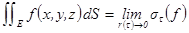, если предел $, при этом 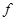наз. инт. по E. Приведем дост. признак инт.: если 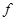непр. на E, то 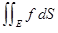существует.

Дата добавления: 2014-01-14