Центральные предельные теоремы

Пусть дана последовательность случайных величин 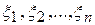, …. Пусть 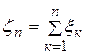- частичная сумма последовательности.

В классической постановке центральные предельные теоремы описывают поведение частичных сумм 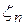, когда n достаточно большое.

В большинстве случаев, будем говорить, что к последовательности случайных величин применима центральная предельная теорема [5], если для любых действительных чисел a < b.

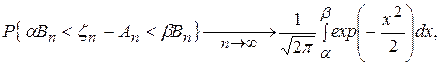(116)

где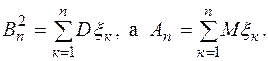

Практически, формула (116) дает оценку вероятности того, что сумма нескольких случайных величин примет значение из заданного интервала. В современных центральных предельных теоремах в качестве предельных распределений рассматриваются распределения, отличные от нормального, обычно это локальные предельные теоремы (распределение Пуассона, Коши распределения, распределение Стьюдента, c² – распределение и др).

Теорема (Линдеберга – Леви). Пусть 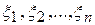,…- последовательность независимых случайных величин, заданных на одном вероятностном пространстве. Пусть существуют

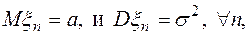
тогда для любых a< b имеет место

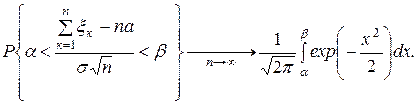
Теорема (Ляпунова). Пусть 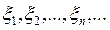- последовательность независимых случайных величин, у которых существуют конечное математическое ожидание - 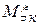, дисперсия - 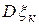и третий центральный момент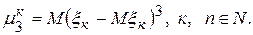

Если 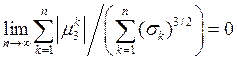, (117)

то закон распределения нормированной суммы

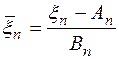
сходится по вероятности к нормальному распределению, то есть

.

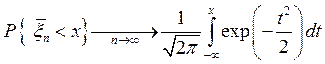Доказательство теорем можно найти в [2,5].

Замечание. Условие (117) означает, что влияние любой из случайных величин x_к последовательности на их сумму несущественно, иначе сходимость определялась бы распределением той случайной величины, у которой дисперсия намного больше, чем у других случайных величин.

Следствие. Если дана последовательность 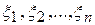,… одинаково распределенных случайных величин с конечной дисперсией, то имеет место сходимость равномерно по х

.

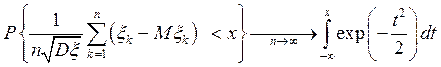Пример 1. В n испытаниях Бернулли с вероятностью успеха р в каждом из испытаний, число успехов можно представить в виде суммы

,

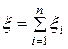где x_i равно единице или нулю, в зависимости от того был ли успех в испытании i или нет (см. теорему Бернулли). Так как испытания независимые, то к сумме применимо следствие из центральной предельной теоремы. Поэтому распределение для x приблизительно нормально, то есть

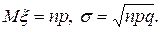
В сущности, это есть теорема Муавра-Лапласа.

Пример 2. На странице 88 рассмотрен пример со случайными величинами , одинаково и равномерно распределенными на [0,1). При рассмотрении сумм 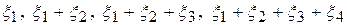, было отмечено, что их плотности тем больше напоминают нормальное, чем больше слагаемых в сумме.

Теперь в силу теоремы Линдеберга-Леви мы можем утверждать, что

,

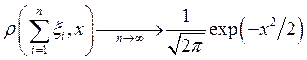где 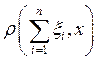- плотность случайной величины .

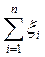Задача. Доказать, что

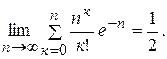
Решение. Воспользуемся следствием к теореме Ляпунова. Предположим, что сл. в. 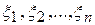,… распределены в соответствии с законом Пуассона, с параметром l =1. В силу следствия, имеем

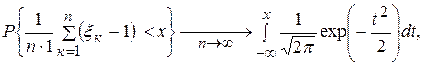
или

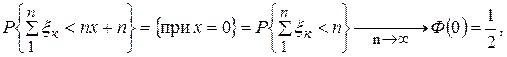
так как

.

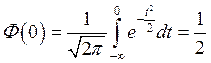Покажем, что

.

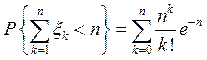Предварительно докажем лемму.

Лемма. Пусть даны случайные величины 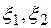, распределенные по закону Пуассона с параметрами 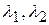, тогда

.

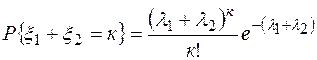Доказательство. Пусть

, ,

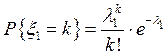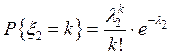тогда 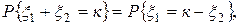к Î N. Отсюда

._▼

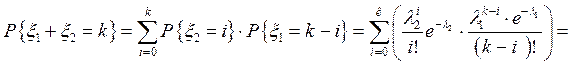
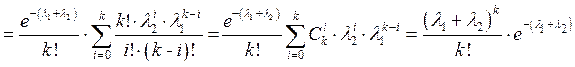Далее, по индукции, легко показать, что, если 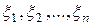распределены по закону Пуассона, то

._▼

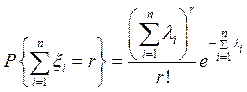Вернемся к задаче.

Рассмотрим событие 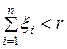. Его можно представить в виде объединения несовместных событий:

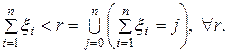
Следовательно, для r = n

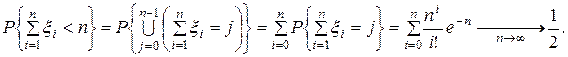
Замечание. Лемма представляет собой пример вычисления свертки дискретных неотрицательных целочисленных случайных величин, распределенных по закону Пуассона.

Практически, центральными предельными теоремами, можно пользоваться и тогда, когда имеется сумма небольшого числа случайных величин (n >10).

В частности, широко применяется приближенная замена одних плотностей на другие, более удобные.

Не следует думать, что все центральные предельные теоремы используют нормальное распределение как предельное. Например, в случайных процессах в качестве предельных рассматриваются c²-распределение, распределение Пуассона, Коши распределение, гамма распределение и др. Эти распределения относятся к классу безгранично делимых распределений (то есть таких, которые представимы как n –кратная свертка (n Î N), одинаковых распределений вероятностей). Доказано, что они и только они могут быть предельными для сумм независимых случайных величин [2]. Рассматриваются также предельные теоремы перехода от дискретных случайных процессов к непрерывным.

Дата добавления: 2014-01-15