Розглянемо ту ж саму задачу, що при застосуванні графічного методу

F = 7x₁ + 5x₂ ® max,

2x₁ + x₂ £ 8,

4x₁ + 5x₂ £ 20,

3x₁ + 8x₂ £ 24,

x₁,x₂ ³ 0

Перейдемо до канонічної форми обмежень, за допомогою уведення додаткових змінних.

2x₁ + x₂ + x₃ = 8,

4x₁ + 5x₂ + x₄ = 20,

3x₁ + 8x₂ + x₅ =24,

x₁, …, x₅ ³ 0.

Симплекс-метод являє собою ітераційну процедуру переходу від поточного опорного плану до наступного з покращеним значенням цільової функції, якщо це можливо. Будемо записувати результати обчислень у таблиці подібній до той, що застосовувалася при розгляданні методу Жордана-Гауса. Перетворимо вираз для цільової функції до форми рівняння з вільним членом у правій частині F = 7x₁ + 5x₂ -F + 7x₁ + 5x₂ = 0. На відміну від раніше застосованої форми будемо праві частини рівнянь записувати у стовпчику, що передує стовпчику x₁. Отримана система обмежень містить у явному вигляді ортонормований базис – це стовпчики x₃, x₄, x₅. Таблиця, що містить результати обчислень, називається симплекс-таблицею. Для поданого прикладу симплекс-таблиця має вигляд табл.6.1.

Табл.6.1.

Баз. змінні	Праві част.	x1	x2	x3	x4	x5
x3							8/2
x4							20/4
x5							24/3
-F

Як бачимо, симплекс-таблиця відображає рівняння задачі. Перші m рядків відображають непрямі обмеження задачі, а останній рядок – вираз для цільової функції. Цей останній рядок називають індексним рядком. Призначення останнього стовпчика розглядається пізніше. Частини стовпчиків x₃, x₄, x₅, відповідаючі рядкам-обмеженням, утворюють базис у трьохвимірному просторі, якому належать стовпці матриці обмежень.

Особливість симплекс-таблиці полягає у тому, що коефіцієнти при базисних змінних у індексному рядку дорівнюють нулю. Форма таблиці з ортонормованим базисом і нульовими коефіцієнтами при базисних змінних у індексному рядку називається приведеною. Симплекс-таблиця дозволяє визначити базисний розв’язок, відповідаючий базису цієї таблиці. Оскільки у опорному плані, усі небазисні змінні дорівнюють нулю, права частина кожного рівняння-обмеження дорівнює значенню відповідної базисної змінної, а права частина у індексному рядку дорівнює -F, тобто значенню цільової функції, взятому з протилежним знаком.

Поданій симплекс-таблиці відповідає опорний план x₁ = x₂ = 0, x₃ = 8, x₄ =20, x₅ =24, на якому цільова функція приймає значення F = 0, оскільки -F = 0.

Визначити, чи поданий опорний план оптимальний, можна проаналізувавши поведінку цільової функції у цій точці. Ця поведінка визначається частинними похідними цільової функції у опорному плані. Якщо праву частину, відповідаючу індексному рядку, позначити через c^’₀, а коефіцієнти при змінних - c^’_j, (j = 1, n), то індексному рядку відповідає рівняння

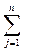
-F + c^’_jx_j = c^’₀. (6.1)

У симплекс-таблиці прикладу (табл.6.1) c^’₀ = 0, c^’_j = c_j для небазисних змінних (j = 1, 2) і c^’_j = 0 для базисних змінних (j = 3, 5).

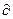
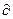З (6.1) отримуємо F/ x_j = c^’_j, j = 1, n. Таким чином, коефіцієнти індексного рядку вказують, значення яких змінних доцільно змінити, щоб покращити значення цільової функції. Оскільки зменшити значення небазисної змінної неможливо (змінні повинні бути невід’ємні), при пошуку максимуму додатні коефіцієнти визначають змінні, значення яких доцільно збільшити. У симплекс-методі перехід до наступного опорного плану здійснюється зміною значення тільки однієї небазисної змінної.

У прикладі індексний рядок містить два додатні коефіцієнти: 7 при x₁ і 5 при x₂. Збільшення будь-якої змінної призведе до збільшення значення цільової функції. Можна сподіватися, що вибір змінної з більшим коефіцієнтом дозволить швидши отримати результат, хоч іноді буває і не так. Вибір небазисної змінної за максимальним коефіцієнтом – це евристичне правило. Отже вибираємо стовпчик x₁, який будемо називати ведучим стовпчиком.

Тепер визначимо, наскільки можна збільшити значення x₁, не порушуючи обмеження задачі. Для того, щоб виконувалися усі рівняння-обмеження при збільшенні x₁, треба зменшувати значення базисної змінної у кожному рівнянні. Мінімальне можливе значення змінної – 0. Ця умова і визначає максимальне можливе значення x₁. З першого рівняння при x₃ = 0 маємо 8 = 2x₁, x₁ = 8/2. Поклавши, у другому рівнянню x₄ = 0, отримуємо 20 = 4x₁, x₁ = 20/4. Нарешті, третє рівняння при x₅ = 0 дає 24 = 3x₁, x₁ = 24/3.

Для того, щоб виконувалися усі обмеження задачі змінна x₁ не повинна перебільшувати мінімальне з трьох визначених. Тому у новому опорному плані x₁ = 8/2 і стає базисною, а змінна x₃ = 0 і стає небазисною. Рядок, якому відповідає нова базисна змінна (у прикладі – перший), називається ведучим рядком, а елемент на перетинанні ведучого стовпця і ведучого рядка – ведучим елементом. Відношення правої частини рядка симплексної таблиці до елементу ведучого стовпця у цьому рядку називається симплексним відношенням. У стовпчик симплекс-таблиці заносяться симплексні відношення.

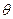При визначенні максимального можливого значення нової базисної змінної враховувалося, що збільшення цієї змінної викликає зменшення старої базисної змінної у кожному рівнянні. Це має місце тільки, якщо коефіцієнт при новій базисній змінній у рівнянні додатній. При нульовому коефіцієнті стара базисна змінна зберігає стале значення, а при від’ємному – збільшується. Отже для визначення ведучого елемента треба обчислювати симплексне відношення тільки для додатніх елементів ведучого стовпця. Якщо ведучий стовпець не містить додатніх елементів, нова базисна змінна може приймати як завгодно великі значення, а це, у свою чергу, означає, що цільова функція не обмежена.

Після визначення ведучого елемента (у прикладі він виділений жирним шрифтом) для вилучення нової базисної змінної з усіх рядків таблиці, крім ведучого, виконується симплексне перетворення. У отриманій симплекс-таблиці аналізується індексний рядок і процесс повторюється доки не буде отриманий індексний рядок без додатніх (від’ємних) коефіцієнтів при пошуку максимуму (мінімуму) або не виявиться, що цільова функція не обмежена. Розв’язування прикладу показано у табл.6.2.

Табл.6.2.

Баз. змінні	Праві част.	x1	x2	x3	x4	x5
x1			1/2	1/2
x4				-2			4/3
x5			13/2	-3/2			24/13
-F	-28		3/2	-7/2
x1	10/3			5/6	-1/6
x2	4/3			-2/3	1/3
x5				17/6	-13/6
-F	-30			-5/2	-1/2

Остання симплекс-таблиця у індексному рядку не містить додатніх коефіцієнтів і тому відповідає оптимальному плану задачі. Згідно з цією таблицею розв’язок задачі становить x₁ = 10/3, x₂ = 4/3, x₃ = x₄ = 0, x₅ =12, а максимальне значення цільової функції F дорівнює 30. Отриманий результат, як бачимо, співпвдає з отриманим графічним методом.

Тепер сформулюємо алгоритм виконання ітерації симплекс-методу.

1. При пошуку максимуму (мінімуму) визначити максимальний (мінімальний) коефіцієнт індексного рядку. Якщо знайдений коефіцієнт дорівнює нулю, поточна симплекс-таблиця оптимальна – алгоритм завершується.

2. Стовпчик, у якому знаходиться знайдений коефіцієнт, вважати ведучим. Якщо у ведучому стовпчику нема додатніх коефіцієнтів, цільова функція не обмежена – задача розв’язку не має - алгоритм завершується.

3. У ведучому стовпчику серед додатніх коефіцієнтів знайти той, якому відповідає мінімальне симплексне відношення, і позначити знайдений коефіцієнт як ведучий елемент.

4. Відносно знайденого ведучого елементу виконати симплексне перетворення поточної симплекс-таблиці.

Дата добавления: 2014-01-13