Построение разностной схемы

Построение разностных схем интегро-интерполяционным методом

Многие динамические задачи практики формулируются в виде основного дифференциального уравнения в частных производных и дополнительных (начальных, граничных) условий, обеспечивающих существование и единственность решения. Под разностной схемой понимают совокупность разностных уравнений, аппроксимирующих основное уравнение и дополнительные условия исходной дифференциальной задачи. Существуют различные способы построения разностных схем. В этом параграфе будет рассмотрен один из способов, носящий название интегро-интерполяционного метода (или метода баланса) построения разностных схем.

В качестве примера рассмотрим применение интегро-интерполяционного метода к построению разностной схемы следующей краевой задачи для обыкновенного дифференциального уравнения второго порядка;

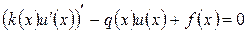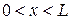, , (1.6)

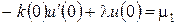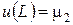, , (1.7)

где 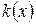, , 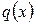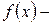заданные достаточно гладкие функции, удовлетворяющие условиям 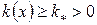, , 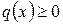, 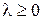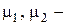заданные числа. При сформулированных условиях существует и единственно решение задачи (1.6), (1.7). Будем считать, что это решение является достаточно гладким.

Для построения разностной схемы введем на отрезке 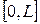равномерную сетку с шагом , т.е. множество точек

.

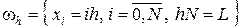Обозначим 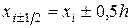, , 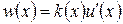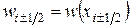и проинтегрируем уравнение (1.6) на отрезке 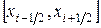. Тогда получим уравнение

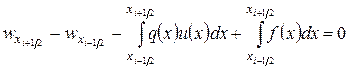. (1.8)

Далее, заменим интеграл

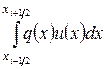
его приближенным значением 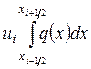и введем обозначение

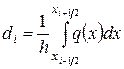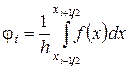, . (1.9)

В результате вместо уравнения (1.8) получим уравнение

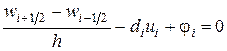. (1.10)

Выразим теперь 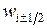через значения функции в точках сетки. Для этого проинтегрируем соотношение 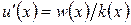на отрезках 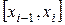и 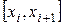. Тогда получим

.

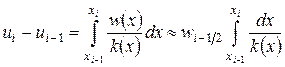Обозначая

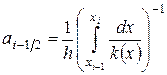, (1.11)

получим .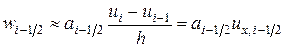

Аналогично .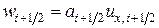

Подставляя эти выражения в уравнение (1.10), получим разностное уравнение, содержащее значения искомой функции в точках , :

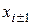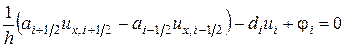. (1.12)

Это уравнение по своему построению является разностным аналогом основного дифференциального уравнения (1.6). Записывая уравнение (1.12) во всех точках сетки, в которых оно определено, т.е. при 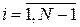, получим систему из 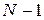линейных алгебраических уравнений относительно 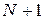неизвестных 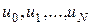. Два недостающих уравнения получаются путем аппроксимации граничных условий (1.7). Одним из этих уравнений является условие , а второе может быть получено интегро-интерполяционным методом. Для этого проинтегрируем основное уравнение (1.6) на отрезк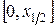е , где :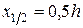

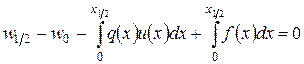. (1.13)

Полагая как и ранее, 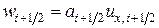, получим при 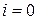, что 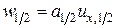. Выражение для 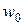следует из граничного условия при 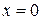: 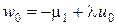. Наконец, полагая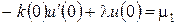

,

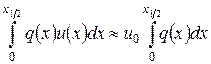получим из тождества (1.13) разностное уравнение

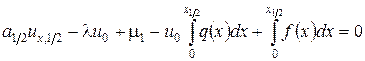. (1.14)

Обозначая

, ,

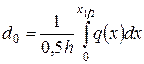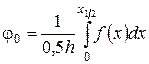перепишем уравнение (1.14) в виде

.

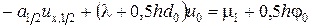Из этой записи видно, что полученное уравнение является разностным аналогом граничного условия (1.7): .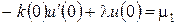

В дальнейшем решение разностной задачи, в отличие от решения дифференциальной задачи, будем обозначать буквой 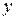, так что 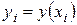, 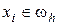. Объединяя все уравнения (1.12) и (1.14), получаем следующую разностную схему для задачи (1.6), (1.7):

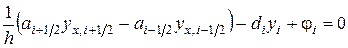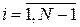, , (1.15)

, .

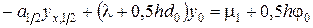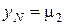При анализе любой разностной схемы возникают следующие вопросы:

1. Существование и единственность системы линейных алгебраических уравнений (1.15).

2. Каким методом надо отыскивать это решение.

3. Какое отношение имеет система разностных уравнений (1.15) к исходной задаче (1.6)-(1.7), иначе говоря, переходит ли разностное уравнение (1.15) в уравнение (1.6), если шаг сетки стремится к нулю?

На первые два вопроса можно ответить немедленно. Разностная задача (1.15) является типичным примером задачи, которая решается методом прогонки. Систему уравнений (1.15) можно записать в виде (доказать)

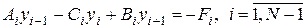, (1.16)

, ,

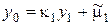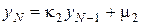где

,

, .

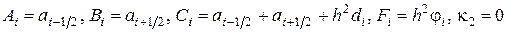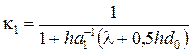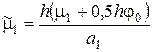Из условий 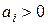, , 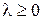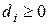следует, что 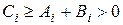, т.е. выполнены условия устойчивости прогонки. Поэтому разностная задача (1.15) однозначно разрешима, и ее можно решать методом прогонки.

Будем искать решение системы (1.16) в виде

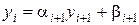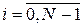, , (1.17)

где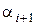, 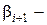неизвестные пока коэффициенты. Отсюда найдем

, .

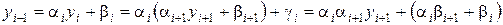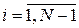Подставляя полученные выражения для 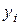, 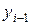в уравнение (1.16), приходим при 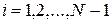к уравнению

.

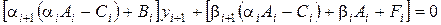Последнее уравнение будет выполнено, если коэффициенты 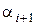, 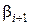выбрать таким образом, чтобы выражения в квадратных скобках обращались в нуль. А именно, достаточно положить

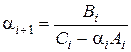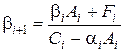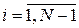, , . (1.18)

Соотношения (1.18) представляют собой нелинейные разностные уравнения первого порядка. Для их решения необходимо задать начальные значения 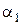, 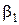. Эти начальные значения находим из требования эквивалентности условия (1.17) при 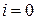, т.е. условия 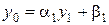, второму из уравнений (1.16). Таким образом, получаем

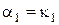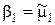, , (1.19)

Нахождение коэффициентов 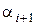, 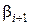по формулам (1.18), (1.19) называется прямой прогонкой. После того как прогоночные коэффициенты 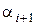, , 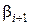, 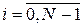найдены, решение системы (1.16) находится по рекуррентной формуле (1.17), начиная с 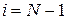. Для начала счета по этой формуле требуется знать 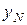, которое определяется из уравнений

, ,

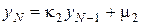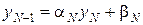откуда

.

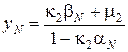Нахождение 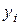по формулам

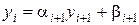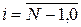, , (1.20)

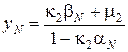
называется обратной прогонкой.

Вопросы аппроксимации и сходимости здесь обсуждаться не будут. Отметим лишь, что интегро-интерполяционный метод при достаточной гладкости коэффициентов 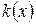, 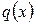и 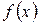имеет второй порядок аппроксимации по , т.е. разностная схема (1.15) сходится и аппроксимирует исходную задачу (1.6) со вторым порядком по .

Дата добавления: 2014-01-13