
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 2. Элементы аналитической геометрии
2.1. Основные формулы аналитической геометрии
Если на плоскости заданы две точки 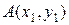 и
и 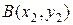 , то расстояние между ними находится по формуле
, то расстояние между ними находится по формуле
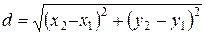 . .
| (2.1) |
Направление отрезка  определяется углом наклона этого отрезка к оси абсцисс. Угол
определяется углом наклона этого отрезка к оси абсцисс. Угол 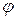 , образованный отрезком
, образованный отрезком  с положительным направлением оси
с положительным направлением оси 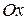 , выражается через координаты концов отрезка по формуле
, выражается через координаты концов отрезка по формуле
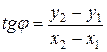 . .
| (2.2) |
Если точка 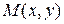 лежит на прямой, проходящей через точки
лежит на прямой, проходящей через точки 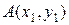 и
и 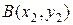 , и дано отношение
, и дано отношение 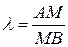 , в котором точка
, в котором точка  делит отрезок
делит отрезок  , то координаты точки
, то координаты точки  определяются следующими формулами:
определяются следующими формулами:
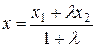 , , 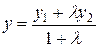 . .
| (2.3) |
В частности, если точка 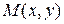 – середина отрезка
– середина отрезка  , то:
, то:
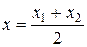 , , 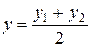 . .
| (2.4) |
Если даны координаты трех вершин треугольника 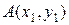 ,
, 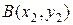 и
и 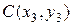 , то площадь треугольника определяется по формуле:
, то площадь треугольника определяется по формуле:
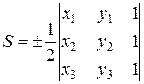 , ,
| (2.5) |
причем знак перед определителем выбирается в зависимости от знака самого определителя так, чтобы число 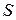 было положительным.
было положительным.
Пример 2.1. На оси ординат найти точку, отстоящую от точки 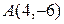 на расстоянии 5 единиц.
на расстоянии 5 единиц.
Решение. Если точка лежит на оси ординат, то ее абсцисса равна нулю, т.е. точка имеет координаты 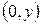 . Определим расстояние между точками
. Определим расстояние между точками 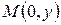 и
и 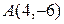 по формуле (2.1)
по формуле (2.1) 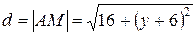 , которое, по условию задачи, равно 5, т.е.
, которое, по условию задачи, равно 5, т.е. 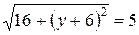 , отсюда следует
, отсюда следует 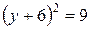 и
и 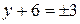 . Значит,
. Значит, 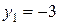 ,
, 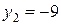 .
.
Итак, существуют две точки 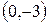 и
и 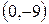 , отстоящие от точки
, отстоящие от точки 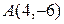 на расстоянии 5 единиц.
на расстоянии 5 единиц.
Пример 2.2. Какой угол образует с осью 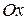 прямая, проходящая через точки
прямая, проходящая через точки 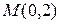 и
и 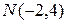 .
.
Решение. Определим тангенс угла, под которым отрезок 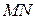 наклонен к оси
наклонен к оси 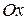 по формуле (3.2):
по формуле (3.2): 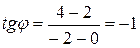 . Эта формула верна при любом расположении точек
. Эта формула верна при любом расположении точек  и
и 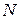 . Таким образом,
. Таким образом, 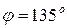 . Угол
. Угол 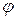 отсчитывается от оси
отсчитывается от оси 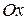 против часовой стрелки.
против часовой стрелки.
Пример 2.3. Даны три вершины параллелограмма 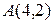 ,
, 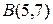 и
и 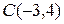 . Найти четвертую вершину
. Найти четвертую вершину 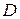 , противоположную вершине
, противоположную вершине 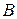 .
.
Решение. Известно, что диагонали параллелограмма в точке пересечения делятся пополам. Поэтому координаты точки 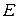 – пересечения диагоналей, найдем как координаты середины отрезка
– пересечения диагоналей, найдем как координаты середины отрезка 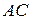 по формуле (2.4):
по формуле (2.4):
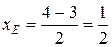 ;
; 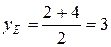 ;
; 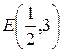 .
.
Зная координаты точки 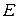 – середины диагонали
– середины диагонали 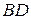 и координаты одного из ее концов
и координаты одного из ее концов 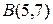 , определим координаты вершины
, определим координаты вершины 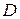 параллелограмма:
параллелограмма:
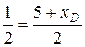 ;
; 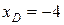 ;
; 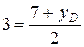 ;
; 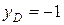 .
.
Итак, вершина 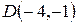 .
.
Пример 2.4. Прямая проходит через точки 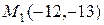 и
и 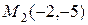 . На этой прямой определить точку, абсцисса которой равна 3.
. На этой прямой определить точку, абсцисса которой равна 3.
Решение. Точка 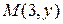 лежит на прямой
лежит на прямой 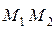 и делит отрезок
и делит отрезок 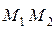 в отношении
в отношении 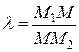 . Зная абсциссу
. Зная абсциссу 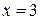 точки
точки  , найдем
, найдем 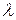 и ординату этой точки по формуле (2.3):
и ординату этой точки по формуле (2.3):
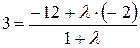 или
или 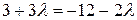 , тогда
, тогда 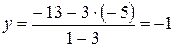 .
.
Итак, 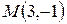 .
.
Пример 2.5. Определить площадь параллелограмма, три вершины которого суть точки 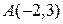 ,
, 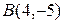 и
и 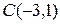 .
.
Решение. Площадь параллелограмма равна удвоенной площади треугольника 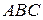 (формула (2.5)):
(формула (2.5)):
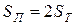 , где
, где 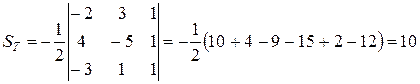 ед.кв.
ед.кв.
Значит, 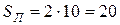 ед.кв.
ед.кв.
2.2. Прямая на плоскости
в прямоугольных координатах уравнение прямой на плоскости задается в одном из следующих видов:
1. Уравнение прямой, проходящей через данную точку перпендикулярно заданному вектору,
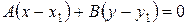 , ,
| (2.6) |
где 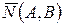 – вектор, перпендикулярный прямой;
– вектор, перпендикулярный прямой; 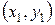 – заданная точка.
– заданная точка.
2. Общее уравнение прямой
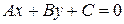 . .
| (2.7) |
3. Уравнение прямой, проходящей через точку в заданном направлении,
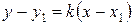 , ,
| (2.8) |
где 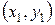 – заданная точка;
– заданная точка; 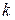 – угловой коэффициент прямой, т.е. тангенс угла, который образует прямая с положительным направлением оси
– угловой коэффициент прямой, т.е. тангенс угла, который образует прямая с положительным направлением оси 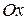 .
.
4. Уравнение прямой, проходящей через две данные точки 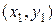 и
и 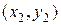 ,
,
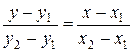 . .
| (2.9) |
5. Уравнение прямой с угловым коэффициентом
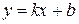 , ,
| (2.10) |
где 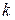 – угловой коэффициент прямой;
– угловой коэффициент прямой; 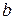 – величина отрезка, отсекаемого прямой на оси ординат.
– величина отрезка, отсекаемого прямой на оси ординат.
6. Уравнение прямой в отрезках на осях
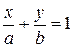 , ,
| (2.11) |
где 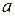 и
и 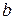 – величины отрезков, которые прямая отсекает на осях координат.
– величины отрезков, которые прямая отсекает на осях координат.
Зная уравнения прямых или точки на них, можно определить:
1. Угловой коэффициент прямой
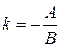 или или 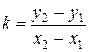 . .
| (2.12) |
2. Угол между прямыми
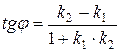 или или 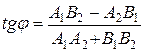 . .
| (2.13) |
3. Условия параллельности двух прямых
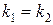 или или 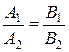 . .
| (2.14) |
4. Условия перпендикулярности прямых
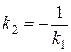 или или 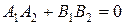 . .
| (2.15) |
5. Расстояние от точки 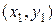 до прямой
до прямой 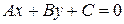
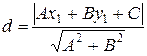 . .
| (2.16) |
Пример 2.6. Найти прямую, проходящую через точки 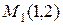 и
и 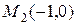 .
.
Решение. Уравнение прямой по формуле (2.9) имеет вид
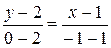 или
или 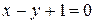 .
.
Пример 2.7. Найти уравнение прямой, проходящей через точку 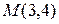 под углом
под углом 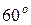 к оси абсцисс.
к оси абсцисс.
Решение. Прямая определена точкой и направлением, где 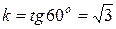 . Искомое уравнение по формуле (2.8) будет
. Искомое уравнение по формуле (2.8) будет
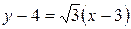 или
или 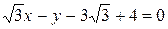 .
.
Пример 2.8. Найти уравнение прямой, проходящей через точку пересечения прямых 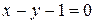 и
и 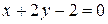 и точку
и точку 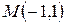 .
.
Решение. Найдем точку пересечения данных прямых, решив систему уравнений
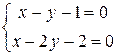
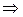
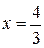 ,
, 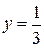 .
.
Точка пересечения прямых 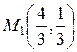 . Уравнение прямой, проходящей через две точки
. Уравнение прямой, проходящей через две точки 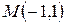 и
и 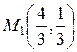 , по формуле (2.9) будет выглядеть так:
, по формуле (2.9) будет выглядеть так:
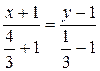 или
или 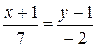 ,
,
откуда получим общее уравнение искомой прямой по формуле (2.7)
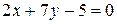 .
.
Пример 2.9. Найти уравнение прямой, которая проходит через точку 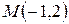 перпендикулярно вектору
перпендикулярно вектору 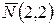 .
.
Решение. Так как прямая проходит через точку 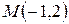 перпендикулярно вектору
перпендикулярно вектору 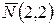 , то воспользуемся уравнением (2.6), подставив в него:
, то воспользуемся уравнением (2.6), подставив в него: 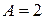 ,
, 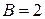 ,
, 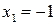 ,
, 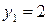 . В результате получим
. В результате получим
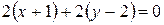 или
или  .
.
Это уравнение прямой является общим (формула 2.7). Для того, чтобы построить прямую по ее уравнению, надо найти координаты двух ее точек. Выбрав 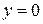 , получим из уравнения прямой
, получим из уравнения прямой 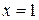 , а полагая
, а полагая 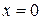 , будем иметь
, будем иметь 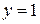 . Прямая пересекает координатные оси в точках
. Прямая пересекает координатные оси в точках 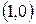 и
и 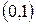 . Строим прямую (рис. 2.1):
. Строим прямую (рис. 2.1):
 у
у
 1
1
 |
1 х
Рис. 2.1 – График прямой
Пример 2.10. Найти уравнение прямой, проходящей через точку 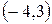 и удаленной от начала координат на расстояние 5 единиц масштаба.
и удаленной от начала координат на расстояние 5 единиц масштаба.
Решение. Уравнение искомой прямой запишем в виде (2.8), подставив вместо 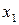 ,
, 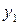 координаты заданной точки. Полученное уравнение
координаты заданной точки. Полученное уравнение 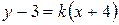 приведем к общему виду (2.7):
приведем к общему виду (2.7):
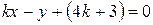 .
.
Начало координат 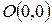 находится на расстоянии 5 единиц от этой прямой. Используя формулу (2.16), получим уравнение для определения коэффициента
находится на расстоянии 5 единиц от этой прямой. Используя формулу (2.16), получим уравнение для определения коэффициента 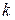 :
:
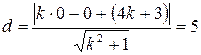 ,
,
откуда 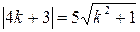 . После возведения в квадрат обеих частей этого уравнения получим
. После возведения в квадрат обеих частей этого уравнения получим
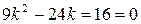 , откуда
, откуда 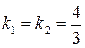 .
.
Следовательно, искомое уравнение запишется так:
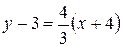 или
или 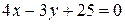 .
.
|
|
Дата добавления: 2014-11-06; Просмотров: 975; Нарушение авторских прав?; Мы поможем в написании вашей работы!