
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Парна лінійна регресія
Лекція №11
Контрольні запитання
1. Яке поняття лежить в основі моделі Неймана? Пояснити зміст даної моделі.
2. У чому полягає відмінність моделі Леонтьєва від моделі Неймана?
3. Які припущення забезпечують змістовність та розв¢язність моделі Неймана?
4. Дати поняття моделі з нульовим прибутком.
5. На які класи поділяють поведінку економічної системи, що описується моделлю Неймана?
6. Яку модель ми називаємо магістральною?
Між фактором 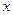 та показником
та показником 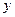 для всієї генеральної сукупностііснує лінійна стохастична залежність
для всієї генеральної сукупностііснує лінійна стохастична залежність 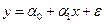 , (1.1)
, (1.1)
де 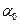 і
і 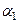 ─ невідомі параметри,
─ невідомі параметри, 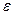 ─ випадкова величина, яка характеризує вплив на показник усіх неврахованих у моделі факторів. Відповідну вибіркову регресійну модель записуємо у вигляді
─ випадкова величина, яка характеризує вплив на показник усіх неврахованих у моделі факторів. Відповідну вибіркову регресійну модель записуємо у вигляді
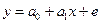 , (1.2)
, (1.2)
де 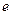 − випадкова величина помилки вибіркової моделі,
− випадкова величина помилки вибіркової моделі, 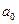 і
і 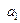 − так звані вибіркові оцінки відповідних генеральних параметрів
− так звані вибіркові оцінки відповідних генеральних параметрів 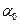 і
і 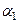 . Вибіркові оцінки, на відміну від генеральних параметрів, є випадковими величинами, так як їх обчислюють на основі обмеженої вибірки. Рівняння виду
. Вибіркові оцінки, на відміну від генеральних параметрів, є випадковими величинами, так як їх обчислюють на основі обмеженої вибірки. Рівняння виду
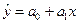 (1.3)
(1.3)
називають парною лінійною регресією.
Для об’єктивної оцінки тісноти лінійної залежності (1.3) між двома змінними 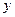 та
та 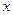 використовуємо коефіцієнт кореляції (коефіцієнт Пірсона). Вибіркову оцінку цього коефіцієнта можна знайти за формулою
використовуємо коефіцієнт кореляції (коефіцієнт Пірсона). Вибіркову оцінку цього коефіцієнта можна знайти за формулою
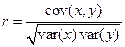 , (1.4)
, (1.4)
в якій
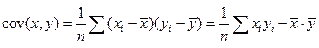 (1.5)
(1.5)
− вибірковий коефіцієнт коваріації між 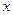 і
і 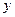 ,
,
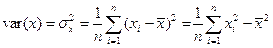 (1.6)
(1.6)
− дисперсія змінної 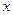 (дисперсію змінної
(дисперсію змінної 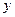 обчислюємо аналогічно),
обчислюємо аналогічно),
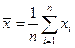 ,
, 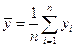 (1.7)
(1.7)
− вибіркові середні значень фактора і показника, 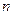 − розмір вибірки.
− розмір вибірки.
Величини
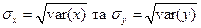 (1.8)
(1.8)
називають середньоквадратичними відхиленнями змінних 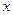 і
і 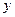 від своїх середніх значень. Можна довести, що
від своїх середніх значень. Можна довести, що 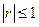 і чим ближче
і чим ближче 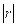 до одиниці, тим сильніший лінійний зв’язок між змінними
до одиниці, тим сильніший лінійний зв’язок між змінними 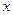 і
і 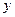 .
.
Оцінки параметрів 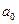 і
і 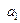 парної регресії обчислюємо за допомогою методу найменших квадратів (МНК) у припущенні, що для генеральної сукупності виконується ряд передумов (яких ми тут не наводимо). В результаті для обчислення цих оцінок отримуємо такі формули:
парної регресії обчислюємо за допомогою методу найменших квадратів (МНК) у припущенні, що для генеральної сукупності виконується ряд передумов (яких ми тут не наводимо). В результаті для обчислення цих оцінок отримуємо такі формули:
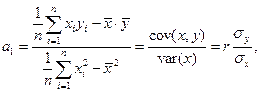
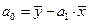 . (1.9)
. (1.9)
Можна довести такі залежності:
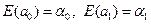 , (1.10)
, (1.10)
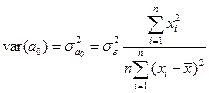 ,
, 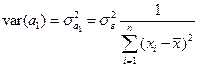 . (1.11)
. (1.11)
У цих формулах буква 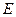 − оператор математичного сподівання,
− оператор математичного сподівання, 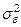 − дисперсія випадкової величини помилки
− дисперсія випадкової величини помилки 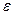 стохастичної залежності (1.1) (зауважимо, що однією з передумов застосування МНК для знаходження оцінок параметрів парної лінійної регресії є умова постійності цієї величини для всіх значень
стохастичної залежності (1.1) (зауважимо, що однією з передумов застосування МНК для знаходження оцінок параметрів парної лінійної регресії є умова постійності цієї величини для всіх значень 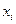 , тобто
, тобто 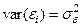 , або інакше це явище називають гомоскедастичністю).
, або інакше це явище називають гомоскедастичністю).
Так як величина помилки 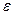 є неспостережуваною випадковою величиною, то ми не можемо знайти
є неспостережуваною випадковою величиною, то ми не можемо знайти 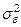 . Тому при обчисленнях використовуємо вибіркову оцінку дисперсії
. Тому при обчисленнях використовуємо вибіркову оцінку дисперсії 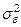 , яку позначаємо
, яку позначаємо 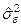 і яку у випадку парної лінійної регресії визначаємо за формулою
і яку у випадку парної лінійної регресії визначаємо за формулою
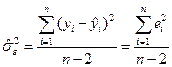 . (1.12)
. (1.12)
Тоді й для параметрів 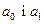 дійсні дисперсії (1.11) замінюємо на їх оцінки
дійсні дисперсії (1.11) замінюємо на їх оцінки
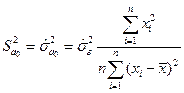 ,
, 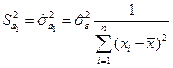 . (1.13)
. (1.13)
Для того, щоб перевірити, чи знайдені за формулами (1.9) оцінки параметрів лінійної регресії статистично значимі, тобто чи значимо вони відрізняються від нуля, щоб стверджувати, що між 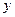 та
та 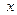 існує лінійна стохастична залежність (1.1) при
існує лінійна стохастична залежність (1.1) при 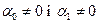 , використовуємо
, використовуємо 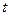 ─ статистику Ст’юдента. Висуваємо нульову й альтернативну гіпотези, які, наприклад, для параметра
─ статистику Ст’юдента. Висуваємо нульову й альтернативну гіпотези, які, наприклад, для параметра 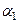 мають вигляд:
мають вигляд:
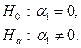 (1.14)
(1.14)
Нульова гіпотеза стверджує, що між 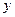 та
та 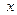 немає лінійної залежності, альтернативна – навпаки, що така залежність існує і зміна
немає лінійної залежності, альтернативна – навпаки, що така залежність існує і зміна 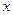 впливає на зміну
впливає на зміну 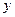 . Для перевірки нульової гіпотези обчислюємо
. Для перевірки нульової гіпотези обчислюємо 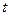 ─ статистику для параметра
─ статистику для параметра 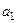 за формулою
за формулою
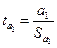 . (1.15)
. (1.15)
Далі вибираємо згідно з умовою задачі 5%-й рівень значимості (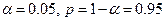 ) і знаходимо за таблицями розподілу Ст’юдента двостороннє значення
) і знаходимо за таблицями розподілу Ст’юдента двостороннє значення 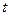 ─ статистики
─ статистики 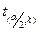 . Зауважимо, що двостороннє значення знаходимо тому, що згідно з альтернативною гіпотезою відхилення
. Зауважимо, що двостороннє значення знаходимо тому, що згідно з альтернативною гіпотезою відхилення 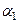 від нуля може бути як у бік від’ємних так і в бік додатних значень і тому перший індекс при
від нуля може бути як у бік від’ємних так і в бік додатних значень і тому перший індекс при 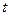 ─
─ 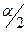 , а не
, а не 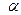 . Другий індекс
. Другий індекс 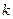 ─ кількість ступенів вільності, яка в нашому випадку дорівнює різниці між розміром вибірки і кількістю оцінених на її основі параметрів, тобто
─ кількість ступенів вільності, яка в нашому випадку дорівнює різниці між розміром вибірки і кількістю оцінених на її основі параметрів, тобто 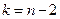 (кількість оцінених параметрів 2). Якщо виявиться, що
(кількість оцінених параметрів 2). Якщо виявиться, що 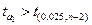 , то на 5%-му рівні значимості нульову гіпотезу
, то на 5%-му рівні значимості нульову гіпотезу 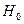 відхиляємо і приймаємо альтернативну
відхиляємо і приймаємо альтернативну 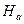 , тобто
, тобто 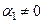 , і між змінними
, і між змінними 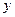 та
та 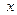 існує лінійна залежність. Ймовірність, що це не так, дорівнює 5%. Аналогічно перевіряємо на значимість параметр
існує лінійна залежність. Ймовірність, що це не так, дорівнює 5%. Аналогічно перевіряємо на значимість параметр 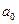 . При цьому
. При цьому 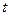 − статистику обчислюємо за формулою
− статистику обчислюємо за формулою
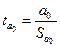 . (1.16)
. (1.16)
Для перевірки тісноти загального зв’язку незалежної та залежної змінних крім коефіцієнта кореляції 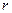 часто використовують коефіцієнт детермінації
часто використовують коефіцієнт детермінації 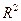 , який показує, яку частку від загальної варіації залишків складає так звана варіація залишків, яка пояснюється через регресійний зв’язок. Коефіцієнт детермінації обчислюють за формулою
, який показує, яку частку від загальної варіації залишків складає так звана варіація залишків, яка пояснюється через регресійний зв’язок. Коефіцієнт детермінації обчислюють за формулою
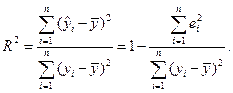 (1.17)
(1.17)
Чим ближчий цей коефіцієнт до одиниці, тим більша варіація залежної змінної 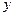 визначається варіацією незалежної змінної
визначається варіацією незалежної змінної 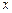 (є тісний зв’язок між залежною та незалежною змінними). Можна довести, що у випадку парної лінійної регресії справедлива формула
(є тісний зв’язок між залежною та незалежною змінними). Можна довести, що у випадку парної лінійної регресії справедлива формула
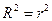 . (1.18)
. (1.18)
Перевірку адекватності прийнятої економетричної моделі статистичним даним здійснюємо також із застосуванням 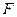 − критерію Фішера. При цьому перевіряємо на значимість тільки параметр
− критерію Фішера. При цьому перевіряємо на значимість тільки параметр 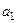 шляхом порівняння варіації, яка пояснюється регресією, з варіацією помилок. Нульова та альтернативна гіпотези, як і за Ст’юдентом, мають вигляд (1.14). Далі обчислюємо випадкову величину так званого
шляхом порівняння варіації, яка пояснюється регресією, з варіацією помилок. Нульова та альтернативна гіпотези, як і за Ст’юдентом, мають вигляд (1.14). Далі обчислюємо випадкову величину так званого 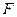 − відношення, яке розподілене за розподілом Фішера з
− відношення, яке розподілене за розподілом Фішера з 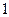 та
та 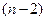 ступенями вільності і визначаємо за формулою
ступенями вільності і визначаємо за формулою
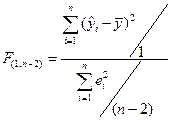 . (1.19)
. (1.19)
В чисельнику і знаменнику цього відношення стоять так звані середні квадрати, які пов’язують відповідні суми квадратів відхилень з їх ступенями вільності. Можна довести справедливість таких рівностей:
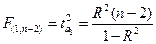 . (1.20)
. (1.20)
Далі задаємо рівень значимості 5% і для цього рівня за статистичними таблицями 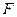 - розподілу Фішера з
- розподілу Фішера з 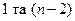 ступенями вільності знаходимо критичне значення
ступенями вільності знаходимо критичне значення 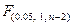 (зауважимо, що в даному випадку перевірку нульової гіпотези проводимо шляхом одностороннього тестування, тому що для прийняття альтернативної гіпотези середній квадрат, зумовлений регресією, повинен бути більшим, ніж середній квадрат помилок). Якщо обчислене нами фактичне значення
(зауважимо, що в даному випадку перевірку нульової гіпотези проводимо шляхом одностороннього тестування, тому що для прийняття альтернативної гіпотези середній квадрат, зумовлений регресією, повинен бути більшим, ніж середній квадрат помилок). Якщо обчислене нами фактичне значення 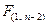 більше за критичне
більше за критичне 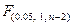 , то відхиляємо нульову гіпотезу, що
, то відхиляємо нульову гіпотезу, що 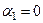 з ризиком помилитися не більше, ніж у 5% випадків.
з ризиком помилитися не більше, ніж у 5% випадків.
Оскільки 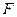 ─ відношення дорівнює квадрату
─ відношення дорівнює квадрату 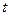 ─ статистики для параметра
─ статистики для параметра 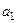 , а
, а 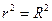 , то
, то 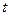 ─ статистику, яка має розподіл Ст’юдента з
─ статистику, яка має розподіл Ст’юдента з 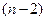 ступенями вільності, можна записати у вигляді
ступенями вільності, можна записати у вигляді
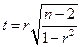 (1.21)
(1.21)
і використати для перевірки на значимість коефіцієнта кореляції 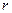 . Якщо позначити коефіцієнт кореляції для генеральної сукупності через
. Якщо позначити коефіцієнт кореляції для генеральної сукупності через 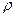 , то нульова й альтернативна гіпотези тоді матимуть вигляд
, то нульова й альтернативна гіпотези тоді матимуть вигляд
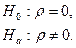 (1.22)
(1.22)
Подальша процедура перевірки повністю співпадає з процедурою перевірки гіпотез (1.14) так як 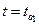 і використовується двостороннє тестування.
і використовується двостороннє тестування.
Таким чином, для парної лінійної регресії перевірка на значимість параметра 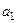 , чи коефіцієнта кореляції
, чи коефіцієнта кореляції 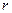 за
за 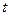 − критерієм Ст’юдента, або перевірка на адекватність прийнятої економетричної моделі статистичним даним за
− критерієм Ст’юдента, або перевірка на адекватність прийнятої економетричної моделі статистичним даним за 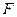 − критерієм – це три модифікації одного і того ж тесту. Тому на практиці необхідно використовувати один із них.
− критерієм – це три модифікації одного і того ж тесту. Тому на практиці необхідно використовувати один із них.
Якщо модель адекватна статистичним даним, то необхідно з надійністю p=0.95 знайти надійні інтервали (інтервали довіри) для генеральних параметрів 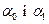 , базисних і прогнозних значень показника.
, базисних і прогнозних значень показника.
Можна довести, що коли деяку величину 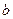 знайдено з використанням МНК на основі випадкової вибірки, взятої з генеральної сукупності з нормальним законом розподілу, то вона також є випадковою величиною з нормальним законом розподілу. Якщо дисперсія випадкової величини
знайдено з використанням МНК на основі випадкової вибірки, взятої з генеральної сукупності з нормальним законом розподілу, то вона також є випадковою величиною з нормальним законом розподілу. Якщо дисперсія випадкової величини 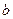 невідома і для неї використовується її вибіркова оцінка
невідома і для неї використовується її вибіркова оцінка 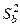 , то для відповідного генерального параметра
, то для відповідного генерального параметра 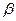 і рівня значимості
і рівня значимості 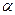 справедлива залежність
справедлива залежність
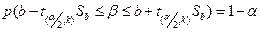 , (1.23)
, (1.23)
тобто з ймовірністю 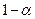 генеральний параметр потрапляє в інтервал
генеральний параметр потрапляє в інтервал
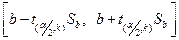 . (1.24)
. (1.24)
Враховуючи це, а також формули (1.13), інтервали довіри для параметрів 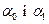 будуть такими:
будуть такими:
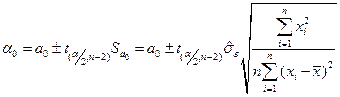 , (1.25)
, (1.25)
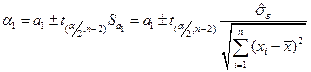 . (1.26)
. (1.26)
Надійні зони для базисних середніх значень показника можна визначати за формулою
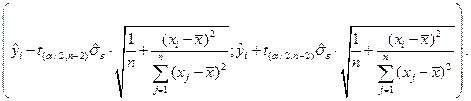 (1.27)
(1.27)
Точковий прогноз при заданому значенні 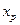 отримуємо шляхом його підстановки в рівняння регресії
отримуємо шляхом його підстановки в рівняння регресії
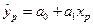 . (1.28)
. (1.28)
Дійсне прогнозне значення 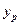 , виходячи з узагальненої моделі (1.1), дорівнює
, виходячи з узагальненої моделі (1.1), дорівнює
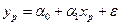 ,
,
де 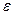 ─ значення неспостережуваної випадкової величини. Оскільки дійсне значення
─ значення неспостережуваної випадкової величини. Оскільки дійсне значення 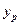 відрізнятиметься від
відрізнятиметься від 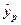 , то потрібно побудувати інтервальний прогноз – інтервал довіри, в який із заданою ймовірністю потрапляє дійсне значення
, то потрібно побудувати інтервальний прогноз – інтервал довіри, в який із заданою ймовірністю потрапляє дійсне значення 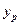 . Такий інтервал будується як для дійсного значення
. Такий інтервал будується як для дійсного значення 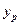 , так і для його математичного сподівання (середнього значення)
, так і для його математичного сподівання (середнього значення) 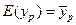 . Інтервал довіри для середнього значення
. Інтервал довіри для середнього значення 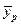 знаходимо за такою ж формулою, як і (1.27), якщо в ній замінити
знаходимо за такою ж формулою, як і (1.27), якщо в ній замінити 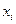 на
на 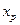 та
та 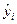 на
на 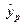 :
:
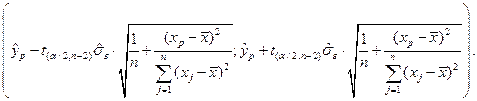 (1.29)
(1.29)
Інтервал довіри для дійсного значення 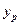 має вигляд
має вигляд
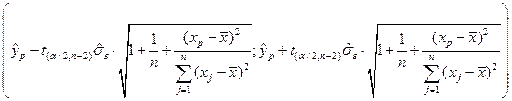 (1.30)
(1.30)
Легко бачити, що варіація для індивідуального значення 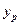 збільшується порівняно з варіацією середнього значення
збільшується порівняно з варіацією середнього значення 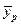 при одному і тому ж значенні
при одному і тому ж значенні 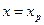 на величину
на величину 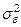 . Це пов’язано з тим, що при використанні МНК
. Це пов’язано з тим, що при використанні МНК 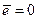 .
.
Для того, щоб визначити міру впливу зміни фактора на зміну показника, використовують коефіцієнт еластичності. Цей коефіцієнт показує, на скільки відсотків зміниться показник 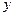 , якщо фактор
, якщо фактор 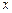 зміниться на 1%. Визначають коефіцієнт еластичності за формулою
зміниться на 1%. Визначають коефіцієнт еластичності за формулою
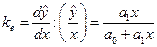 . (1.31)
. (1.31)
Як бачимо з формули (1.31), коефіцієнт еластичності в загальному випадку залежить від фактора 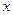 . Надаючи
. Надаючи 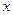 базисних значень
базисних значень 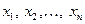 , отримаємо відповідні значення коефіцієнта еластичності, які можна наочно зобразити у вигляді графіка. Коефіцієнт еластичності для прогнозу отримаємо в результаті підстановки замість
, отримаємо відповідні значення коефіцієнта еластичності, які можна наочно зобразити у вигляді графіка. Коефіцієнт еластичності для прогнозу отримаємо в результаті підстановки замість 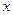 в (1.31) значення
в (1.31) значення 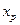 .
.
Перевірку залишків 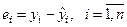 на автокореляцію здійснюють за допомогою критерію Дарбіна-Уотсона. Коротко суть його полягає в наступному.
на автокореляцію здійснюють за допомогою критерію Дарбіна-Уотсона. Коротко суть його полягає в наступному.
Припускається наявність автокореляції першого порядку у вигляді
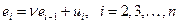 ,
,
де 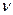 − коефіцієнт автокореляції, для якого припускаємо виконання умови
− коефіцієнт автокореляції, для якого припускаємо виконання умови 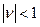 і вважаємо, що для залишків
і вважаємо, що для залишків 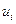 автокореляція відсутня. В цьому випадку можна за допомого МНК знайти таку оцінку для коефіцієнта автокореляції
автокореляція відсутня. В цьому випадку можна за допомого МНК знайти таку оцінку для коефіцієнта автокореляції 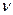 :
:
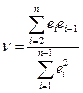 .
.
Статистику Дарбіна-Уотсона обчислюємо за формулою
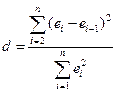 (1.32)
(1.32)
і можна довести, що між нею і коефіцієнтом автокореляції існує приблизна залежність
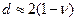 . (1.33)
. (1.33)
Якщо автокореляція відсутня, то 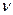 близьке до нуля і статистика Дарбіна-Уотсона набуває значень, які близькі до 2. Якщо автокореляція додатна, то
близьке до нуля і статистика Дарбіна-Уотсона набуває значень, які близькі до 2. Якщо автокореляція додатна, то 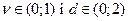 . Якщо ж автокореляція від’ємна, то
. Якщо ж автокореляція від’ємна, то 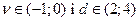 . Очевидно, що коли
. Очевидно, що коли 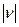 близький до нуля, то автокореляція відсутня, якщо
близький до нуля, то автокореляція відсутня, якщо 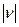 близький до одиниці, то наявна сильна автокореляція і якщо
близький до одиниці, то наявна сильна автокореляція і якщо 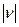 близький до 0.5, то важко судити про наявність чи відсутність автокореляції. Тому для
близький до 0.5, то важко судити про наявність чи відсутність автокореляції. Тому для 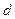 ─ статистики визначені критичні межі (
─ статистики визначені критичні межі (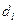 ─ нижня,
─ нижня, 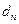 ─ верхня), які дозволяють із заданою надійністю дати відповідь, чи можна прийняти гіпотезу про відсутність автокореляції першого порядку, чи ні.
─ верхня), які дозволяють із заданою надійністю дати відповідь, чи можна прийняти гіпотезу про відсутність автокореляції першого порядку, чи ні.
Отже, залежно від значення 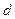 приймаємо:
приймаємо:
1) якщо 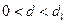 ряд залишків додатно автокорельований;
ряд залишків додатно автокорельований;
2) якщо 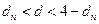 ряд не містить автокореляцію;
ряд не містить автокореляцію;
3) якщо 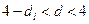 ряд відхилень від’ємно автокорельований;
ряд відхилень від’ємно автокорельований;
4) якщо 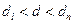 або
або 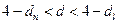 необхідні подальші дослідження
необхідні подальші дослідження
 |
Рис.1.3
Аналіз результатів показує, що побудована модель згідно з усіма критеріями є адекватною спостережуваним даним. Найбільша зміна показника при зміні фактора на один відсоток спостерігається при великих значеннях фактора і досягає 0.6 відсотка. Однак статистика Дарбіна-Уотсона знаходиться в межах
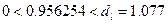 ,
,
що свідчить про наявність незначної додатної автокореляції залишків першого роду. Це означає, що застосування методу найменших квадратів у даному випадку є не зовсім коректним і для знаходження оцінок параметрів парної лінійної регресії потрібно використовувати інші методи (зокрема метод Ейткена).
Література
1. Вітлінський В. В. Моделювання економіки: Навчальний посібник.— К.: КНЕУ, 2003. — 408 с.
2. Колемаев В. А. Математическая экономика: Учебник для вузов.— М.: ЮНИТИ, 1998. — 240 с.
3. Малыхин В. И. Математическое моделирование экономики: Учеб.- практ. пособие. — М.: УРАО, 1998. — 160 с.
4. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В. В. Федосеев и др.; Под ред. В. В. Федосеева. — М.: ЮНИТИ, 1999. — 391 с.
5. Шелобаев С. И. Математические методы и модели в экономике, финансах, бизнесе: Учеб. пособие для вузов. — М.: ЮНИТИ ДАНА, 2000. — 367 с.
6. Пономаренко О. І., Перестюк М. О., Бурим В. М. Основи математичної економіки. — К.: Інформтехніка, 1995. — 320 с.
7. Нейман фон Дж., Моргенштерн О. Теория игр и экономическое поведение. — М.: Наука, 1970. — 700 с.
8. Канторович Л. В. Экономический расчёт наилучшего использования ресурсов. — М.: Из-во АН СССР, 1959. — 344 с.
9. Ланкастер К. Математическая экономика. — М.: Сов. радио, 1972. — 464 с.
Зміст
| Вступ…………………………………………………………………….. | |
| Лекція №1. Моделювання поведінки споживача.................................. | |
| Лекція №2. Рівняння Слуцького............................................................. | |
| Лекція №3. Моделі поведінки виробників............................................. | |
| Лекція №4. Поняття виробничої функції............................................... | |
| Лекція №5. Моделі взаємодії споживачів та виробників..................... | |
| Лекція №6. Динамічна модель міжгалузевого балансу........................ | |
| Лекція №7. Класична модель ринкової економіки............................... | |
| Лекція №8. Модель Солоу....................................................................... | |
| Лекція №9. Модель міжгалузевого балансу (модель Леонтьєва)........ | |
| Лекція №10. Модель Неймана................................................................ | |
| Лекція №11. Парна лінійна регресія…………………………………... | |
| Література.................................................................................................. |
|
|
Дата добавления: 2014-12-08; Просмотров: 3976; Нарушение авторских прав?; Мы поможем в написании вашей работы!