Моделювання сезонних явищ і процесів

Для деяких економічних процесів характерні періодичні коливання з певною тривалістю періодів. Якщо періоди коливань мають тривалість один рік, то такі коливання називають сезонними. Для них характерні закономірності, які регулярно повторяються із місяця в місяць, із кварталу в квартал. Сезонні коливання притаманні виробництву сільськогосподарської продукції, попиту на окремі товари, завантаженню транспорту, будівельному виробництву тощо.

Існує декілька способів дослідження сезонних коливань, серед яких найпоширенішим на практиці вважають спосіб розрахунку сезонних показників, який ґрунтується на визначенні тенденції за допомогою плинної середньої і методу найменших квадратів.

Кількісним показником, який вказує на наявність сезонних коливань, є індекс сезонності, який обчислюють за формулою:

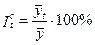, (5.39)

де 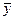– середній рівень ряду динаміки за рік;

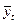– середній рівень ряду динаміки за інтервал часу t (місяць або квартал).

Аналіз сезонних коливань вимагає використання даних за декілька років, оскільки окремі коливання можуть бути зумовлені випадковими факторами і не матимуть закономірного характеру, а плинна середня, яку застосовують для виявлення тренду, повинна мати строго визначений період згладжування – 12 місяців, або 4 квартали. Оскільки середні плинні стосуються певного місяця, то при 12 і 4-членному згладжуванні здійснюють центрування.

Індекс сезонності можна визначати як відношення фактичного рівня до рівня, розрахованого за середньою плинною, яку вважають вільною від сезонних коливань. У такому разі передбачається, що сезонний фактор постійно впливає на значення показника, оскільки при обчисленні індексу переважно елімінуються випадкові фактори. Повне елімінування впливу несезонних факторів досягається лише тоді, коли середня із індексів сезонності дорівнює 1.

Після того, як визначені індекси сезонності, можна обчислити значення рівнів динамічного ряду, в яких еліміновано вплив сезонності (десезоналізовані) рівні.

Приклад 5.4. Обсяги виробництва продукції фірмою за 11 кварталів показано в табл.5.8.

Таблиця 5.8

Кількість виробництва продукції, тис. шт.
Квартал
Рік

Розрахувати індекси сезонності, визначити сезонні компоненти.

Результати розрахунків представлені в табл.5.9. Обчислення середніх значень індексів сезонності наведено в табл.5.10.

Таблиця 5.9

Поряд- ковий номер року	Квартал	Кількість вироб- ництва, тис.шт..	Разом за 4 квар-тали	Середня плинна за 4 квартали	Центро-вана середня плинна	Індекс сезон-ності	Середнє значення індекса сезонності	Десезона-лізований випуск
				-			0,9604	20,8
			-			1,0649	24,4
				27,5	1,1273	1,1389	27,2
				30,5	0,8852	0,8358	32,3

Продовження табл.5.9

					33,5	0,9552	0,9604	33,3
				35,5	1,0704	1,0649	35,7
					1,1622	1,1389	37,8
					0,7949	0,8358	37,1
						0,9756	0,9604	41,7
			-			1,0649	43,2
			-			1,1389	44,8

Таблиця 5.10

Квартал	Середнє значення індекса сезонності	Відкориговане середнє значення індекса
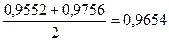
		0,9604
	1,0704	1,0649
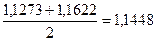
		1,1389
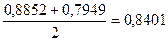
		0,8358

На підставі десезоналізованих обсягів випуску продукції можна побудувати лінійне рівняння регресії, яке характеризує значення рівнів динамічного ряду без урахування сезонності:

.

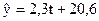Загалом модель ряду динаміки, для якого характерні сезонні коливання, можна представити виразом:

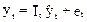, (5.40)

де 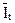– середній індекс сезонності для періоду t;

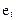– випадкова величина.

Крім моделей, що ґрунтуються на розкладі ряду динаміки на складові компоненти, для дослідження процесів, яким притаманний сезонний характер, можна використовувати моделі сезонної хвилі, які побудовані на підставі гармонійного аналізу. Модель сезонної хвилі має вигляд:

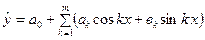, (5.41)

де 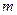– кількість гармонік багаточлена.

Гармоніка – це синусоїдальна або косинусоїдальна функція з певним періодом. Знаходження кінцевої суми гармонік називають гармонійним аналізом. Кількість гармонік не повинна перевищувати значення 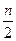. З практичної точки зору модель сезонної хвилі добре описується декількома першими гармоніками. Дисперсія, яка відповідає кожній з гармонік, становить:

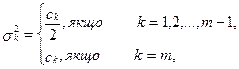
де .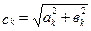

Частка дисперсії, яка враховується k-ю гармонікою у загальній дисперсії, подається відношенням 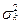до загальної дисперсії 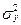. Дисперсії, які враховуються різними гармоніками, додаються, оскільки ніякі дві гармоніки не корелюють між собою.

Змінна х в моделі сезонної хвилі (5.41) вимірюється в градусах або радіанах. За даними щомісячного спостереження сезонного явища впродовж року аргумент х як фактор часу може набувати значення від 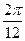до .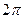

Застосування методу найменших квадратів забезпечує знаходження невідомих параметрів рівняння регресії періодичного вигляду (5.41) за такими формулами:

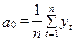; (5.42)

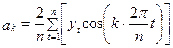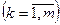, ; (5.43)

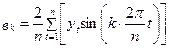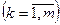, . (5.44)

5.4. Автокореляційний аналіз. Авторегресійні моделі

Між рівнями динамічного ряду може існувати кореляційна залежність, яку називають автокореляцією. Наприклад, різкий спад обсягу виробництва, який мав місце в одному з періодів, тривалий час може негативно впливати на значення наступних рівнів динамічного ряду. Оцінка залежності між послідовними рівнями динамічного ряду проводиться за допомогою коефіцієнтів автокореляції:

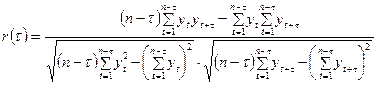(5.45)

Коефіцієнт r 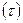характеризує щільність зв’язку між послідовними спостереженнями ряду динаміки 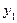, ,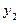…, 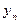та 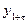, ,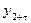…, 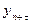(зміщеними один відносно іншого на 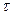одиниць) і називається коефіцієнтом автокореляції з часовим лагом 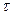. Коефіцієнт автокореляції змінюється в межах від –1 до +1. Коефіцієнт автокореляції, близький за абсолютним значенням до одиниці, вказує на щільну залежність між фактичним і зсуненим рядами, а близький до нуля – на їхню незалежність.

Послідовність значень коефіцієнтів автокореляції 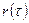утворює автокореляційну функцію, аналіз якої забезпечує достатньо глибоке уявлення про внутрішню структуру досліджуваного ряду динаміки. Із зростанням 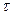(порядку автокореляції) кількість корельованих пар зменшується, а у разі великої кількості спостережень значущими виявляються лише високі коефіцієнти автокореляції. З практичного погляду (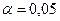) можна стверджувати, що коефіцієнт автокореляції 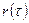буде статистично значущим, якщо його абсолютне значення перевищує 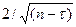, тобто 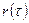лежить за межами довірчих границь значущості. Під час розрахунку автокореляційної функції потрібно враховувати ту обставину, що із збільшенням 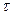кількість пар 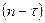спостережень 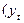, 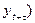зменшується. Тому лаг 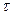необхідно вибирати таким, щоб величина 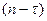була достатньою для знаходження 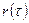. У практичних дослідженнях враховують умову, що максимальне значення 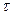не повинно перевищувати величину .

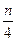Графік автокореляційної функції називають корелограмою. Корелограма наочно показує, як зміни попередніх рівнів впливають на наступні рівні ряду динаміки. На рис.5.1 наведена типова корелограма стаціонарного ряду, для якого індивідуальні значення коливаються навколо середнього значення, не виявляючи при цьому ні істотної тенденції зміни середнього, ні сезонних особливостей. У зміні значень коефіцієнтів автокореляції відсутня певна закономірність, і жоден з них не лежить за межами паралельних прямих, що визначають довірчі границі значущості.

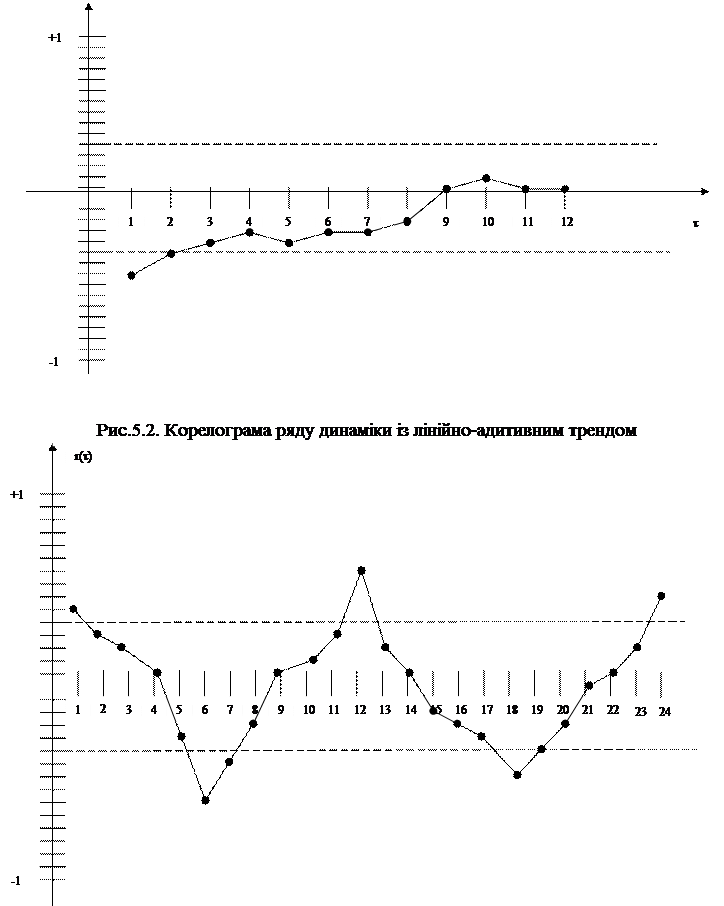
Типова корелограма ряду динаміки з лінійно-адитивним трендом (зростання середнього значення відбувається приблизно на однакову величину для кожного моменту часу) наведена на рис.5.2. Візуальний аналіз корелограми вказує на залежність значень коефіцієнта автокореляції від величини лагу. Із зростанням лагу значення коефіцієнтів автокореляції зменшуються, а максимальне значення (за абсолютною величиною) відповідає лагу 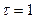, причому значущим є лише коефіцієнт автокореляції 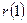. Якщо від корелограми початкового ряду динаміки перейти до корелограми перших різниць, то строга лінійна залежність зникне і спостерігатиметься сукупність хаотично розкиданих точок між прямими, що визначають границі значущості коефіцієнтів автокореляції.

Корелограма із сезонним характером тренду показана на рис.5.3. Для сезонних явищ спостерігається щільна кореляційна залежність між рівнями ряду динаміки, що відповідають одному і тому ж місяцю. Порівняно високі значення 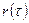при 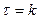, , 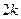,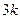… свідчать про те, що в динамічному ряді відзначаються регулярні сезонні коливання. Найбільші значення коефіцієнта автокореляції відповідають лагам 12 і 24 (причому обидва вони є статистично значущими). Найменші значення приймають коефіцієнти r(6) та r(18), які є також статистично значущими, і відповідають порівнянням спостережень піків підйому і спаду.

τ

	Рис.5.3. Корелограма ряду динаміки із сезонним трендом

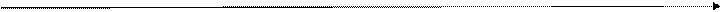
Для аналізу рядів динаміки, зокрема під час дослідження випадкових компонент статистичних моделей, важливим є дослідження стаціонарності залишків 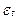. Ряд називають стаціонарним, якщо його властивості (закон розподілу і числові характеристики) не змінюються в часі. У разі стаціонарності ряду із зростанням лагу 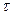взаємозв’язок між рівнями послаблюється і автокореляційна функція 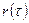спадає (за абсолютним значенням). Якщо формально побудована корелограма не є функцією, що швидко спадає, то це, як правило, свідчить про нестаціонарність ряду.

Автокореляцію між випадковими складовими характеризує циклічний коефіцієнт автокореляції першого порядку:

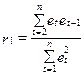, (5.46)

де 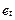- залишкові величини.

Обчислене значення 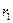порівнюють з критичним для вибраного рівня значущості 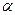(табл.5.11). Якщо розрахункове значення є меншим за критичне, то автокореляція вважається неістотною, а випадкова компонента відображає стаціонарний випадковий процес. У протилежному разі необхідно зробити висновок про неадекватність детермінованої складової (тренду) реальному процесу.

Таблиця 5.11

Критичні значення циклічного коефіцієнта автокореляції (α=0,05)

n	Додатні значення	Від’ємні значення	n	Додатні значення	Від’ємні значення
	0,253	-0,753		0,299	-0,399
	0,345	-0,708		0,276	-0,356
	0,370	-0,674		0,257	-0,356
	0,371	-0,625		0,242	-0,300
	0,366	-0,593		0,229	-0,279
	0,360	-0,564		0,208	-0,248
	0,353	-0,539		0,191	-0,225
	0,348	-0,516		0,178	-0,207
	0,341	-0,497		0,170	-0,195
	0,335	-0,479		0,161	-0,184
	0,328	-0,462			-0,174

У розглянутих моделях аналітичного вирівнювання рядів динаміки як регресор (пояснювальну змінну) вибирали незалежну змінну t. Проте часто для досліджуваного ряду динаміки не вдається підібрати адекватну модель, для якої залишки 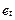задовольняють основні припущення регресійного аналізу.

У практиці статистичного моделювання широко застосовують регресійні моделі, в яких регресорами є змінні, значення яких впливає на результативний показник з деяким запізненням (лагові змінні). Характерною особливістю рівнів ряду динаміки у таких моделях є те, що в них відстежується механізм впливу попередніх результатів на наступні. Наприклад, для ряду динаміки, який описує послідовні значення курсу акцій, доцільно вважати, що результати попередніх торгів будуть мати вплив на результати наступних (якщо в певний момент курс акцій виявиться завищеним порівняно з реальним, то швидше за все, він буде завищеним і на наступних торгах).

Моделі, в яких значення рівнів динамічного ряду в момент t подано залежністю від значень рівнів у попередні моменти t-1, t-2,..., t-p, називають авторегресійними моделями p-го порядку (модель АR (p)):

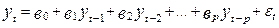(5.47)

Частковим випадком моделі АR (p) є авторегресійна модель 1-го порядку АR (1):

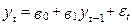(5.48)

Для побудови авторегресійної моделі важливим є вирішення питання про її порядок. Якщо порядок авторегресійної моделі є низьким, то можна отримати результати, які не є статистично значущими, оскільки не використовується важлива інформація за попередні моменти часу. З іншого боку, підвищення порядку авторегресійної моделі може призвести до зниження якості моделі. Тому на практиці будують декілька моделей, на підставі яких визначають потрібний порядок. При цьому досліджуються автокореляційні функції, використовуються статистичні критерії. Оцінювання параметрів авторегресійних моделей і моделей плинної середньої проводиться за допомогою методів, описаних у попередньому параграфі посібника (зокрема, 1МНК).

Приклад 5.5. На підставі ряду динаміки, що характеризує зміну курсу акцій компанії (табл.5.12), побудувати авторегресійну модель 1-го порядку.

Таблиця 5.12

t
уt, грн.
t
уt, грн.
t
уt, грн.
t
уt, грн.

Користуючись стандартною функцією ЛИНЕЙН системи EXCEL отримуємо авторегресійну модель 1-го порядку:

.

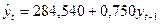Розрахункове значення F-критерію рівне 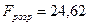. Оскільки F_розр>F_кр=4,35 (для рівня значущості α=0,05), можна зробити висновок про адекватність моделі.

За формулою (5.46) отримуємо значення циклічного коефіцієнта автокореляції першого порядку r₁=0,122, яке є меншим за критичне, що вибране з табл.5.11. Тому автокореляцію вважаємо неістотною, а випадкову компоненту такою, що утворює стаціонарний випадковий процес.

Крім авторегресійних моделей, для моделювання рядів динаміки використовують моделі, в яких рівень динаміки в момент t задається лінійною функцією від залишків:

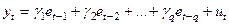, (5.49)

де 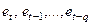- відхилення теоретичних рівнів ряду динаміки від фактичних; 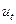- випадкова (залишкова) компонента моделі; 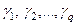- невідомі коефіцієнти при відхиленнях.

Модель (5.49) називають моделлю плинної середньої q-порядку (модель МА(q)). Необхідно зауважити, що термін “плинна середня” у даному випадку не ототожнюється з аналогічним терміном, який розглядається при згладжуванні рядів динаміки.

У практиці моделювання рядів динаміки застосовують комбінування моделей АR і МА – модель АRМА(p, q):

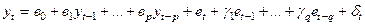. (5.50)

де 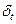- випадкова компонента моделі.

Авторегресійні моделі і моделі плинної середньої використовують для моделювання стаціонарних рядів динаміки. Якщо ж ряд динаміки є нестаціонарним, то необхідно застосувати процедуру приведення нестаціонарного ряду до стаціонарного, зміст якої полягає у використанні різниць між рівнями ряду. Сам порядок різниць визначається характером тренду. Моделі, побудовані на основі значень різниць, прийнято називати моделями Бокса-Дженкінса.

Дата добавления: 2014-12-16