Элементы комбинаторики. 1 страница

Размещения: Пусть из множества 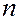элементов выбираются элементов. Такая комбинация с учетом порядка записи и называется размещением. Число размещений определяется формулой

ПРИМЕР: Сколькими способами можно набрать семизначный номер телефона, если все цифры разные?

Перестановка – произвольная упорядоченная запись 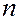элементов. Число перестановок определяется формулой

Выпишем перестановки из трех элементов.

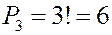
ПРИМЕР: Сколькими способами можно разместить четверых гостей и хозяина за столом?

Сочетания. Пусть из множества 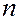элементов выбираются элементов. Любая такая комбинация без учета порядка записи и называется сочетанием. Число сочетаний равно

ПРИМЕР: Сколькими способами можно из 20 присяжных отобрать трех для участия в судебном процессе?

Алгебра событий.

Пространством элементарных событий называется множество всех элементарных исходов, относящихся к заданному опыту.

Суммой ( или объединением ) двух событий называется событие, которому благоприятствуют исходы, благоприятствующие событиям или .

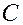ПРИМЕР. При подбрасывании игрального кубика событие - выпало четное число, является суммой трех событий: - выпала “2”; - выпала “4”; - выпала “6”.

События и называются несовместными, если нет элементарных исходов, благоприятствующих этим двум событиям одновременно.

ПРИМЕР. При подбрасывании игрального кубика событие - выпало четное число и событие - выпала “3” несовместны, а события 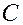- выпало нечетное число и - выпала “5” совместные.

ТЕОРЕМА. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

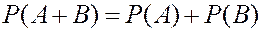
ПРИМЕР. В урне находятся 2 белых, 3 красных и 5 синих одинаковых по размеру шаров. Какова вероятность, что шар, случайным образом извлеченный из урны, будет цветным (не белым)?

Пусть событие - извлечение красного шара,

событие - извлечение синего шара.

Событие - извлечение цветного шара.

Так как события и несовместны (извлекается только один шар), то по теореме сложения

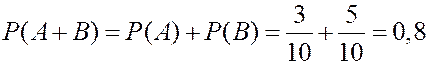
Произведением ( или пересечением ) двух событий называется событие, которому благоприятствуют исходы, благоприятствующие одновременно событиям и .

ПРИМЕР. При подбрасывании игрального кубика событие - выпало “5”, ¾ является произведением двух событий: события - выпало нечетное число очков; и события 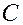- выпало больше трех очков.

Событие называется противоположным событию , если событию благоприятствуют все те элементарные исходы, которые не являются благоприятствующими для события .

ПРИМЕР. При подбрасывании игрального кубика событие - выпало четное число очков, является противоположным событию - выпало нечетное число очков.

ТЕОРЕМА. Сумма вероятностей противоположных событий равна единице.

ПРИМЕР. Если вероятность попадания в цель при одном выстреле , то вероятность промаха

.

ЗАДАЧА. При проверке качества деталей, выпущенных на заводе, в среднем из 100 деталей оказывается 85 деталей первого сорта и 10 деталей второго сорта. Найти вероятность того, что взятая наудачу деталь окажется бракованной.

- деталь качественная,

- деталь бракованная,

- деталь первого сорта,

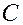- деталь второго сорта.

Вероятности событий и 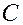нам заданы

Найдем вероятность того, что деталь бракованная.

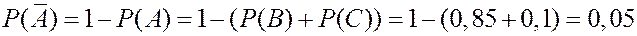ТЕОРЕМА. Если события и совместны, вероятность суммы событий равна сумме вероятностей этих событий без вероятности их совместного появления.

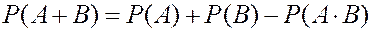
ЗАДАЧА. Из 20 студентов группы 5 не сдали экзамен по математике, 4 – по информатике, причем 3 получили двойки по двум предметам. Какова вероятность, что случайно выбранный студент будет успевающим?

- студент не имеет двоек,

- студент имеет двойку по математике,

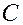- студент имеет двойку по информатике.

Вероятности событий известны

Тогда вероятность того, что случайно выбранный студент будет неуспевающим

А нам необходимо найти вероятность противоположного события. Так как получим

Условная вероятность.

Иногда необходимо определить вероятность случайного события , при условии что произошло. То, что произошло, сужает пространство элементарных исходов.

Пусть множество состоит из 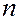равновозможных исходов. Событию благоприятствуют исходов, событию благоприятствуют исходов. Тогда

Условная вероятность события , при условии что произошло есть вероятность события в новом вероятностном пространстве . Условная вероятность обозначается как или .

Если событие произошло, реализовался один из исходов. То есть множеством всех элементарных исходов для будет , а множеством благоприятных исходов .

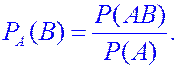
ЗАДАЧА. Из 30 экзаменационных билетов студент знает 25. Если он отказался отвечать по первому билету, ему разрешают взять второй. Определить вероятность того, что второй билет ему известен.

РЕШЕНИЕ. Пусть событие - первый билет “плохой”

событие - второй билет “хороший”.

Если произошло событие , из 30 билетов осталось 29, причем известных студенту по-прежнему 25.

ТЕОРЕМА. Вероятность произведения двух событий равна произведению вероятности одного события на условную вероятность другого, при условии, что первое уже произошло.

Эта теорема может быть обобщена на любое число множителей.

ЗАДАЧА. Студент знает 25 из 30 экзаменационных вопросов. Экзамен сдан, если он ответит на три вопроса билета.

РЕШЕНИЕ. Пусть событие - ответил на первый вопрос,

- ответил на второй вопрос,

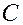- ответил на третий вопрос.

События и называются независимыми, если условная вероятность при условии наступления события равна безусловной.

ТЕОРЕМА. Если события и независимы, вероятность их произведения равна произведению вероятностей.

ЗАДАЧА. Двумя стрелками производится по одному выстрелу по мишени. Вероятности попадания 0,8 и 0,9 соответственно. Найти вероятность того, что оба стрелка попадут в мишень.

РЕШЕНИЕ. События - попадание первого стрелка, и - попадание второго стрелка, независимы, Таким образом

Формула полной вероятности.

Система событий 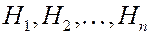называется полной группой событий для данного испытания, если любым исходом опыта является одно и только одно событие этой группы. Таким образом, событие достоверно, то есть , и события и попарно несовместны, то есть .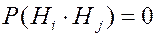

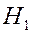
Пусть событие может произойти в результате появления одного и только одного события из полной группы событий. События этой группы обычно называют гипотезами.

ТЕОРЕМА. Вероятность события равна сумме произведений вероятностей всех гипотез, образующих полную группу, на соответствующие вероятности события .

ЗАДАЧА. В партии из 600 электрических лампочек 200 лампочек изготовлены на первом заводе, 250 на втором и 150 на третьем. Известны также вероятности 0.95, 0.91, 0.93 того, что лампочка окажется стандартного качества при изготовлении её соответственно первым, вторым и третьим заводами. Какова вероятность, что наудачу выбранная из данной партии лампочка окажется стандартной?

РЕШЕНИЕ. Пусть событие - лампочка оказалась стандартной.

Событие может произойти, если выполнена одна из гипотез.

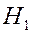- лампочка изготовлена на первом заводе,

- на втором заводе,

- на третьем заводе.

Вероятности гипотез:

.

Условные вероятности события :

Тогда полная вероятность события равна

Формула Байеса.

Имеется полная группа несовместных гипотез 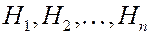, вероятности которых известны до опыта (априори). Производится опыт, в результате которого зарегистрировано появление события , причем этому событию гипотезы приписывали определенные вероятности . Необходимо переоценить вероятности гипотез после опыта (апостериори), то есть нужно определить условные вероятности .

По теореме умножения вероятностей имеем:

.

Отсюда следует, что

,

где находим по формуле полной вероятности.

ЗАДАЧА. Пусть при массовом производстве некоторого изделия вероятность того, что оно окажется стандартным, 0.95. Для контроля производится проверка стандартности, которая даёт положительный результат в 99% случаев для стандартных изделий и в 3% случаев для нестандартных. Какова вероятность стандартности изделия, выдержавшего проверку?

РЕШЕНИЕ. Событие - изделие выдержало проверку. Событие может произойти, если выполнена одна из гипотез.

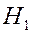- изделие стандартное,

- изделие нестандартное.

Вероятности гипотез:

.

Условные вероятности события :

Тогда полная вероятность события

Повторение опытов.

Пусть производится серия испытаний. В результате каждого отдельного опыта событие А появляется с определенной вероятностью. Нас интересует число появлений события А в серии. Пусть опыты независимы и вероятность появления события А в каждом опыте постоянна.

Схема Бернулли.

Поскольку вероятность 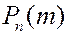представляется членами разложения бинома , то распределение называется биномиальным.

Задача. Вероятность заболеть гриппом равна 0,4. Найти наивероятнейшее число заболеваний гриппом из 5 сотрудников отдела.

Решение.

.

,

,

,

,

.

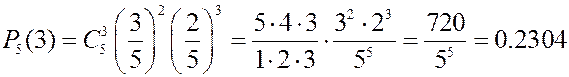Таким образом, с наибольшей вероятностью заболеет 2 сотрудника.

Локальная теорема Муавра-Лапласа.

Вычисление вероятности 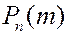по формуле Бернулли становится затруднительным при больших 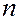, поскольку . Поэтому на практике применяют приближенные формулы. Одна из них формула Муавра-Лапласа.

где

Функция - четная: ; достигает максимума в точке . При этом быстро стремится к нулю с увеличением абсолютной величины :

ЗАДАЧА. Найти вероятность того, что событие наступит 75 раз в 400 испытаниях, если .

РЕШЕНИЕ.

Сравним с точным значением

.

Интегральная формула Муавра-Лапласа.

Если нас интересует вероятность того, что в серии из 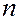испытаний событие появится не менее и не более раз, то

где

Здесь - функция Лапласа. Функция нечетная . При возрастании от 0 до функция быстро возрастает почти до 0,5. , . Можно считать при всех .

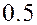
Дата добавления: 2014-12-07