Задачи и упражнения для самостоятельной работы

(по темам 2 и 3)

Задача 1

Ниже приведены данные о количестве членов семьи в 50 обследованных фермерских хозяйствах:

1. Построить дискретный вариационный ряд — распределение 50 хозяйств по количеству членов семьи.

2. Изобразить ряд графически с помощью полигона распределения.

Задача 2

Имеются следующие данные об урожайности озимой пшеницы в 40 обследованных хозяйствах:

27,1 18,2 16,3 22,0 24,3 24,8 33,0 27,3

28,5 15,1 19,5 28,1 25,1 26,7 28,4 29,6

23,7 18,0 31,0 19,8 26,0 23,5 20,2 25,1

22,8 27,0 20,4 24,0 29,5 22,9 19,9 27,0

25,3 23,9 21,5 23,1 21,1 22,6 25,8 23,8

1. Определить размах вариации урожайности (х mах-х min).

2. Построить интервальный вариационный ряд с равными интервалами, выделив 6 групп хозяйств по величине урожайности.

3. Изобразить ряд графически с помощью гистограммы распределения.

4. По накопленным частотам построить кумуляту распределения 40 хозяйств по величине урожайности.

Задача 3

Определить (назвать) вид приводимых ниже таблиц, их подлежащее и сказуемое.

а) Группировка промышленных предприятий РФ
по объекту продукции в 2010 г.

Группы предприятий с объемом продукции, млрд. руб.	Число предприятий, % к итогу	Объем продукции, % к итогу	Среднегодовая численность промышленно-производственного персонала, % к итогу
До 1 1,1−50 50,1−100 Свыше 100	84,0 14,2 1,7 0,1	3,6 16,2 37,3 42,9	13,1 34,4 36,9 15, 6
Всего	100,0

б) Распределение численности безработных в РФ
по возрастным группам (на конец октября 2010 г.)

Возрастная группа, лет	Численность безработных, % к итогу
	мужчины	женщины
16—19 20—24 25—29 30—49 50—54 55—59 60—72	7,7 11,9 50,9 4,2 5,7 2,6	11,2 18,5 11,7 49,5 3,8 1,3
Итого	100,0	100,0

в) Основные показатели промышленности РФ
за 2004-2010 гг.

Год
Число предприятий, тыс.	26,9	28,0	61,1
Численность промышленно- производствённого персонала, млн чел.	21.0	20,1	20,0	18,8	17,4	16,0	14,9
Уровень рентабельности продукции, %	12,0	27,1	38,3	32,0	19,5	20,1	9,2

Задача 4

1. По данным таблицы «а» из задачи 3 построить кривую Лоренца для числа предприятий (%) и объема продукции (%), а также рассчитать коэффициент Джини, характеризующий степень концентрации объема продукции по выделенным группам предприятий.

2. То же самое проделать для числа предприятий (%) и численности промышленно-производственного персонала.

Ответ: 1) 0,922; 2) 0,780.

Задача 5

Имеются следующие данные по предприятиям промышленности РФ за 2010 г.

Группы предприятий с численностью промышленно - производственного персонала, чел.	Число предприятий, % к итогу	Объем продукции, % к итогу
До 200 201—500 Свыше 500	93,6 3,4	12,7 9,6 77,7
Итого

1. Построить кривую Лоренца для распределения объема продукции по группам предприятий с разной численностью персонала.

2. С помощью коэффициента Джини определить уровень (степень) концентрации объема продукции по выделенным группам предприятий.

Ответ: 2) 0,833.

Тема 4

ОТНОСИТЕЛЬНЫЕ И СРЕДНИЕ ВЕЛИЧИНЫ

Относительные и средние величины – основные обобщающие показатели, используемые при анализе статических данных.

Изучение относительных величин обычно не вызывает у студентов затруднений. Надо уметь в каждом отдельном случае правильно выбрать форму относительной величины (простое кратное отношение, процентное, промильное или продецимильное выражение); следует помнить о необходимости соблюдения условия сопоставимости данных, на основе которых рассчитываются относительные величины выполнения плана, динамики, сравнения.

Знакомясь со средними величинами, следует помнить, что средние должны рассчитываться лишь для качественно однородных совокупностей. Кроме того, в зависимости от исходных данных сред­ние значения тех или иных признаков могут рассчитываться по-разному. Очень часто среднее значение какого-либо показателя вычисляется в статистике на основе итоговых показателей, рассчитанных для совокупности. Так, например, зная валовой сбор и посевную площадь под зерновыми по области, легко определить среднюю урожайность зерновых, разделив валовой сбор на посевную площадь. Если же известны значения признака у отдельных единиц совокуп­ности, то осредненный показатель может быть рассчитан как сред­няя из отдельных вариантов по одной из формул различных видов средних величин, в одних случаях — как средняя арифметическая (простая или взвешенная), в других — как средняя гармоническая (простая или взвешенная), в третьих — как средняя геометрическая и т. д.

Из средних величин наиболее часто встречаются средняя арифметическая простая 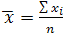и средняя арифметическая взвешенная 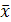= 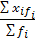, где x_i — отдельные значения признака, варианты; f_i — веса каждого варианта. Взвешенная применяется в тех случаях, когда отдельные значения признаков повторяются. Если вместо абсолютных частот в распределении имеются частости (w_i), выступающие в роли весов, то тогда 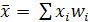(если wi выражены в доля, 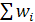= 1) или 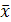= 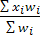, (если w_i выражены в процентах, 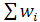= 100).

Рассмотрим ряд примеров.

Задача 4.1

Пусть имеются следующие данные о производстве продукта А рабочими бригады за смену:

Номер рабочего
Произведено продукции A за смену, шт., х.

Нужно определить среднюю выработку одного рабочего данной бригады.

Последняя определяется как средняя арифметическая простая:

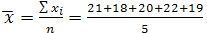= 20 (шт.)

Задача 4.2

Имеется следующее распределение 60 рабочих по тарифному разряду:

Тарифный разряд xi
Число рабочих fi

Нужно определить средний тарифный разряд рабочих. Расчет производим по средней арифметической взвешенной:

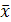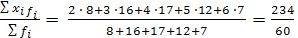= = 3,9.

Для интервальных рядов сначала находят центры (середины) интервалов, а затем последние умножают на веса, произведения сум­мируют и делят на сумму весов.

Задача 4.3

Требуется определить среднемесячную заработную плату одного рабочего по следующим данным (графы 1 и 2 таблицы):

Месячная заработная плата, руб.	Число рабочих fi	Середина интервала xi	Xi fi
400-500 500-­600 600-­700 700-­800 800­-900 900-1000
Итого		­

Среднее значение признака (x_i) в каждом интервале дано в графе 3. Результаты умножения вариантов (x_i) на веса (f_i) показаны в графе 4.

Отсюда средняя заработная плата одного рабочего

=

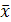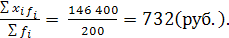
Примечание. В целях упрощения вычислений при больших зна­чениях x_i последние можно уменьшить, помня, что всякое уменьше­ние вариантов (x_i) влечет за собой соответствующее уменьшение средней арифметической и что поэтому после вычисления средней арифметической из уменьшенных вариантов следует увеличить ее «во столько раз» и «на столько», «во сколько» и «на сколько» уменьша­лись варианты. Этот прием расчета покажем на примере дальше (см. задачу 5.4).

Когда весами у отдельных признаков служат показатели, явля­ющиеся произведением этих вариантов на количество единиц, то средняя из всех вариантов рассчитывается как средняя гармоничес­кая взвешенная, формула которой

= .

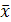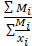Задача 4.4

Предположим, по пяти хозяйствам имеются данные об урожай­ности зерновых и валовом сборе:

Хозяйство	Урожайность зерновых, ц/га, xi	Валовой сбор зерна, ц, Mi
		18 000
		30 000
		63 000
		44 000
		30 000
∑	—	185 000

Нужно рассчитать среднюю урожайность для всех хозяйств. Для решения задачи следует валовой сбор всех хозяйств разделить на общую площадь. Площадь по каждому хозяйству неизвестна, но лег­ко может быть рассчитана путем деления валового сбора на урожайность. Произведя последовательно все расчеты, получим среднюю урожайность:

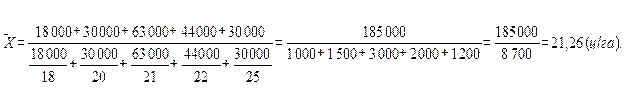
Если урожайность обозначить через х_i, а валовой сбор через М_i, то нетрудно убедиться, что расчет средней урожайности произведен по средней гармонической взвешенной 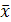= 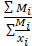. Если бы валовой сбор был везде одинаков, то значения весов в числителе и зна­менателе сократились бы и, можно было бы воспользоваться средней гармонической простой:

= .

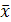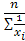Кроме средней арифметической и средней гармонической в статистике применяют и другие виды средних (геометрическая, квадратическая и др.). Их использование будет показано в дальнейших темах.

Контрольные вопросы

1. Какова роль относительных величин в статистике?

2. Какие существуют формы выражения относительных вели­чин?

3. Как классифицируются относительные величины по их по­знавательному значению?

4. Каково значение средних величин в статистике?

5. Какие виды средних величин применяются в статистике?

6. Как исчисляются средние арифметические: простая и взве­шенная?

7. В каких случаях применяется средняя гармоническая?

Тема 5

МОДА, МЕДИАНА И ДРУГИЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА

В статистике недостаточно знать лишь среднюю величину того или иного признака у единиц совокупности. Большой интерес при статистическом исследовании различных совокупностей представля­ет изучение вариации (колеблемости) признака у отдельных единиц и характера распределения единиц по данному признаку.

Вариации признака и характер распределения изучаются преж­де всего с помощью некоторых характеристик вариационного ряда, из которых рассмотренная ранее средняя арифметическая является основной, характеризующей центр группирования. Другими харак­теристиками центра группирования являются мода (М_о) и медиана (Me).

Мода (наиболее часто встречающееся значение признака у единиц совокупности) для дискретного ряда определяется непосредственно как вариант (х), имеющий наибольшую частоту или частость (в вариационном ряду задачи 4.2 из предыдущей темы Мо равняется 4). Для интервального ряда с равными интервалами мода рассчитывается по формуле

M_о = x₀ + h ,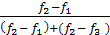

где x₀— начальная (нижняя) граница модального интервала;

h — величина интервала;

f₂ — частота модального интервала;

f₁ — частота интервала, предшествующего модальному;

f₃ — частота интервала, следующего за модальным.

Задача 5.1

Определить моду по данным задачи 4.3. В условии задачи 4.3 наибольшую частоту (60) имеет интервал (700—800). Отсюда

Мо =700 + 100 ,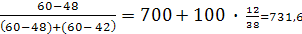

т. е. наиболее часто встречается заработная плата в размере 731,6 руб.

В ряду с неравными интервалами мода определяется в интервале, имеющем наибольшую плотность распределения, и в формуле вместо f₁, f₂, f₃ принимаются соответствующие плотности распределения.

Для нахождения медианы (значения признака у средней единицы ранжированного ряда) сначала определяется ее порядковый номер (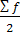), а затем по накопленным частотам определяется либо сама медиана (для дискретных рядов), либо медианный интервал (для интервальных рядов), в котором путем простой интерполяции рассчитывается значение медианы по формуле

Me = x₀ + h ,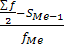

где x₀ — нижняя граница медианного интервала;

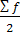— порядковый номер медианы;

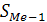— накопленная частота до медианного интервала;

— частота медианного интервала.

Задача 5.2

Для приведенного в задаче 4.3 распределения рабочих по разме­ру заработной платы определить медиану.

Перепишем этот ряд и рассчитаем в нем накопленные частоты:

Месячная заработная плата, руб.	Число рабочих, fi	Накопленные частоты, S
400−500
500−600
600−700
700−800
800−900
900−1000
Итого		—

Определяем порядковый номер медианы:

N_Me= .

По накопленным частотам видно, что сотая единица находится в интервале (700-800), ее значение определяем по формуле

Me=700+100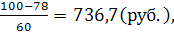

т. е. делаем вывод по медиане, что половина рабочих получает заработную плату ниже 736,7 руб., а половина — выше.

Мода и медиана могут быть определены графически: первая — по гистограмме, а вторая — по кумуляте.

Дата добавления: 2014-12-24