
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Робота сили ваги 7 страница
|
|
|
|
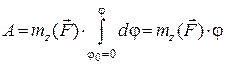 . (28.20)
. (28.20)
Отже, робота сталої за модулем сили, прикладеної до твердого тіла, що обертається навколо нерухомої осі, дорівнює добутку моменту цієї сили відносно осі обертання на відповідний кут повороту тіла.
Потужність сили дорівнює добутку моменту сили відносно осі обертання на кутову швидкість обертання:
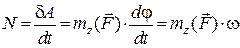 . (28.21)
. (28.21)
Лекція 29
Теореми про зміну кінетичної енергії
матеріальної точки і механічної системи.
ЗАКОН ЗБЕРЕЖЕННЯ ПОВНОЇ МЕХАНІЧНОЇ ЕНЕРГІЇ
29.1. Теорема про зміну кінетичної енергії матеріальної точки
Розглянемо рух матеріальної точки  під дією сили
під дією сили  зі зміною швидкості
зі зміною швидкості 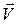 (рис. 29.1).
(рис. 29.1).
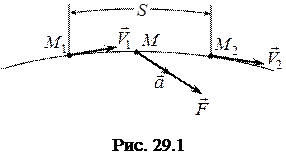 Основне рівняння руху точки має вигляд:
Основне рівняння руху точки має вигляд:
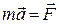 ,
,
або
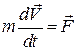 . (29.1)
. (29.1)
Знайдемо скалярний добуток рівності (29.1) на вектор 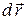 :
: 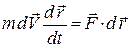 ,
,
або
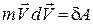 . (29.2)
. (29.2)
Оскільки
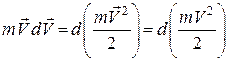 ,
,
тоді остаточно маємо:
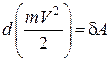 . (29.3)
. (29.3)
Скалярна величина, яка дорівнює половині добутку маситочки на квадрат її швидкості називається кінетичною енергією матеріальної точки, тобто  .
.
Кінетична енергія матеріальної точки є другою скалярною мірою механічного руху. Одиницею кінетичної енергії є 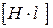 .
.
Рівняння (29.3) визначає теорему про зміну кінетичної енергії матеріальної точки в диференціальній формі
Диференціал кінетичної енергії матеріальної точки дорівнює елементарній роботі сили, яка діє на матеріальну точку
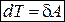 . (29.4)
. (29.4)
Зінтегруємо обидві частини рівняння (29.2) вздовж усього переміщення 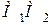 :
:
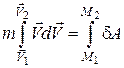 ,
,
звідки
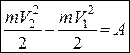 . (29.5)
. (29.5)
Рівняння (29.5) визначає теорему про зміну кінетичної енергії матеріальної точки в скінченій (інтегральній) формі
Зміна кінетичної енергії матеріальної точки на будь-якому переміщенні дорівнює роботі сили, яка діє на точку, на тому самому переміщенні.
29.2. Закон збереження повної механічної енергії матеріальної точки при дії на неї потенціальних сил:
|
|
|
Якщо матеріальна система рухається у потенціальному силовому полі під впливом консервативних сил, то сума її кінетичної і потенціальної енергії (повна механічна енергія) є сталою величиною.
Припустимо, що матеріальна точка рухається в потенціальному полі, а сила, що діє на цю точку, є консервативною.
Як відомо з теорії поля, елементарна робота консервативної сили, що діє на матеріальну точку, дорівнює диференціалу потенціальної енергії з від’ємним знаком:
 . (29.6)
. (29.6)
Тому теоремі про зміну кінетичної енергії для цієї точки у диференціальній формі можна надати вигляду
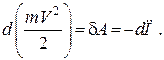 (29.7)
(29.7)
Інтегруючи обидві частини цієї рівності, отримаємо
 . (29.8)
. (29.8)
Тут  – стала інтегрування, що має назву сталої енергії.
– стала інтегрування, що має назву сталої енергії.
Позначивши 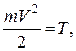 остаточно маємо:
остаточно маємо:
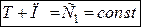 . (29.9)
. (29.9)
Рівняння (29.9 ) називається інтегралом повної механічної енергії.
Рівності (29.9) можна надати іншого вигляду:
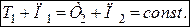 (29.10)
(29.10)
Тут 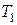 і
і 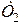 та
та 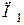 і
і 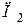 – величини кінетичної і потенціальної енергій точки в положеннях
– величини кінетичної і потенціальної енергій точки в положеннях  і
і 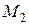 .
.
У законі збереження механічної енергії йдеться про перетворення кінетичної енергії в потенціальну і навпаки.
29.3. Теорема про зміну кінетичної енергії механічної системи
Кінетичною енергією механічної системи називається скалярна величина  , яка дорівнює сумі кінетичних енергій усіх точок цієї системи:
, яка дорівнює сумі кінетичних енергій усіх точок цієї системи:
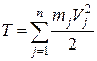 . (29.11)
. (29.11)
Головна відмінність величини  від введених раніше величин
від введених раніше величин 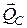 і
і 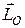 полягає в тому, що кінетична енергія є величиною скалярною і додатною.
полягає в тому, що кінетична енергія є величиною скалярною і додатною.
Розглянемо рух механічної системи під дією зовнішніх сил 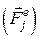 і внутрішніх сил
і внутрішніх сил 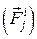 .
.
Застосуємо до кожної j- ої точки даної механічної системи теорему про зміну її кінетичної енергії:
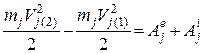
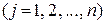 .
.
Записавши таких рівнянь стільки, скільки точок має дана система. Підсумуємо їх:
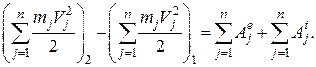
Позначимо:
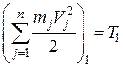 ;
; 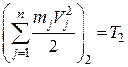 .
.
Тут 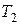 і
і 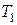 – кінетична енергія механічної системи відповідно в кінці і на початку шляху.
– кінетична енергія механічної системи відповідно в кінці і на початку шляху.
Отже, остаточно маємо:
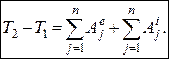 (29.12)
(29.12)
Рівняння (29.12 ) визначає теорему про зміну кінетичної енергії механічної системи:
|
|
|
Зміна кінетичної енергії механічної системина деякому переміщенні дорівнює сумі робіт усіх зовнішніх і внутрішніх сил, прикладених до точок системи, на тому самому переміщенні.
Якщо механічна система є незмінною або абсолютно твердим тілом, тоді 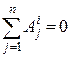 , і рівняння (29.12) буде мати такий вигляд:
, і рівняння (29.12) буде мати такий вигляд:
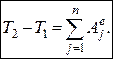 (29.13)
(29.13)
29.4. Обчислення кінетичної енергії механічної системи в залежності від виду її руху
І. При поступальному русі всі точки механічної системи мають однакові швидкості, які дорівнюють швидкості центра мас  , тоді
, тоді
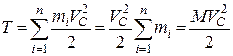
Кінетична енергія механічної системи, при її поступальному русі дорівнює половині добутку маси системи на квадрат швидкості її центра мас:
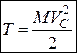 . (29.14)
. (29.14)
ІІ. При обертальному русі механічної системи навколо нерухомої осі швидкість довільної її точки 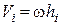 . Тут
. Тут 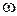 – кутова швидкість системи;
– кутова швидкість системи; 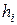 – відстань від точки до осі обертання. Тоді для кінетичної енергії маємо:
– відстань від точки до осі обертання. Тоді для кінетичної енергії маємо:
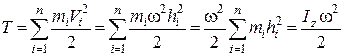
Кінетична енергія механічної системи при її обертальному русі дорівнює половині добутку моменту інерції системи відносно осі обертання на квадрат кутової швидкості обертання системи:
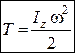 . (29.15)
. (29.15)
ІІІ. Плоскопаралельний рух механічної системи у кожний момент часу можна розглядати як миттєво обертальний навколо миттєвої осі, що проходить через миттєвий центр швидкостей (т. Р). Отже, кінетична енергія системи може бути визначена за формулою (27.15).
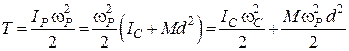 . (29.16)
. (29.16)
Тут 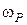 – миттєва кутова швидкість обертання навколо миттєвої осі, яка дорівнює кутовій швидкості
– миттєва кутова швидкість обертання навколо миттєвої осі, яка дорівнює кутовій швидкості 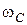 обертання навколо центральної осі
обертання навколо центральної осі 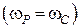 ;
;  – момент інерції механічної системи відносно миттєвої осі обертання;
– момент інерції механічної системи відносно миттєвої осі обертання; 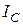 – момент інерції механічної системи відносно центральної осі
– момент інерції механічної системи відносно центральної осі 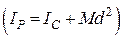 ; d – відстань між миттєвим центром швидкостей і центром мас.
; d – відстань між миттєвим центром швидкостей і центром мас.
Враховуючи, що 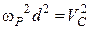 , остаточно з (29.16) маємо:
, остаточно з (29.16) маємо:
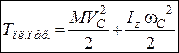 . (29.17)
. (29.17)
Кінетична енергія механічної системи при її плоско-паралельному русі дорівнює сумі двох доданків, один з яких дорівнює кінетичній енергії системи при поступальному русі разом з центром мас, а другий – кінетичній енергії системи при її обертальному русі навколо рухомої осі, що проходить через центр мас, перпендикулярно до площини його руху хОу (рис.29.2).
Це є частинний випадок відповідної теореми Кьоніга.
Розділ ХІV. ДИНАМІКА ТВЕРДОГО ТІЛА В ЗАЛЕЖНОСТІ ВІД ТИПУ ЙОГО РУХУ
|
|
|
Лекція 30
Динаміка твердого тіла при поступальному,
обертальному і плоскопарелельному русі
30.1. Диференціальні рівняння поступального руху твердого тіла
Для розв’язування задач динаміки необхідно вміти складати диференціальні рівняння в залежності від виду руху твердого тіла. Основою для отримання таких рівнянь є загальні теореми динаміки механічної системи.
При поступальному русі твердого тіла всі його точки (включаючи центр мас) мають геометрично рівні швидкості та прискорення.
Отже, використовуючи теорему про рух центра мас, можемо записати:
 , де
, де  . (30.1)
. (30.1)
Проектуючи векторне рівняння (30.1) на декартові координатні осі, маємо:
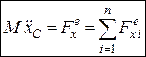 ,
, 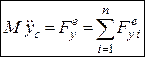 ,
, 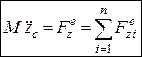 . (30.2)
. (30.2)
Рівняння (30.2) єдиференціальними рівняннями поступального руху твердого тіла. За їх допомогою можна розв’язувати дві основні задачі щодо поступального руху твердого тіла:
1. За заданим законом руху твердого тіла певної маси визначати головний вектор всіх зовнішніх сил, які діють на точки цього тіла
2. За заданими зовнішніми силами і початковими умовами визначити рівняння руху твердого тіла певної маси.
30.2. Диференціальне рівняння обертального руху твердого тіла навколо нерухомої осі
Розглянемо обертання твердого тіла навколо нерухомої осі під дією зовнішніх сил 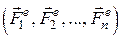 (рис. 30.1). Застосуємо принцип звільнення від в’язей.
(рис. 30.1). Застосуємо принцип звільнення від в’язей.
Запишемо теорему про зміну кінетичного моменту механічної системи в проекціях на вісь 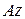 :
:
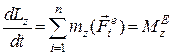 . (30.3)
. (30.3)
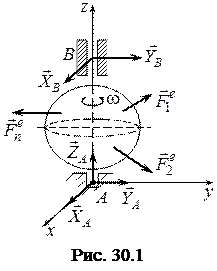 Якщо розглядати обертання тіла за відсутністю сил тертя, то сума моментів реакцій в’язей відносно осі
Якщо розглядати обертання тіла за відсутністю сил тертя, то сума моментів реакцій в’язей відносно осі 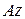 дорівнюватиме нулю і в праву частину рівняння увійдуть моменти лише тих сил, що задаються.
дорівнюватиме нулю і в праву частину рівняння увійдуть моменти лише тих сил, що задаються.
Характеристикою інертності тіла при обертальному русі є момент інерції тіла відносно осі обертання 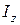 .
.
Перетворимо ліву частину рівняння (30.3), враховуючи, що  :
:
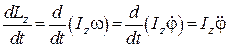 .
.
Тоді рівняння (30.3) матиме такий вигляд:
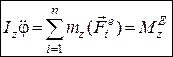 , (30.4)
, (30.4)
або
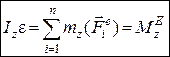 . (30.4.а)
. (30.4.а)
Рівняння (30.4) є диференціальним рівнянням обертального руху тіла навколо нерухомої осі, що дозволяє розв’язувати такі задачі:
1. За заданим законом обертання тіла 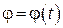 і його моментом інерції
і його моментом інерції 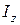 визначати головний момент зовнішніх сил
визначати головний момент зовнішніх сил 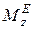 , що діють на тверде тіло.
, що діють на тверде тіло.
|
|
|
2. За заданими зовнішніми силами, моментом інерції тіла і початковими умовами обертання визначати закон обертального руху тіла.
3. За заданими зовнішніми силами і кутовим прискоренням тіла 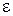 визначити момент інерції
визначити момент інерції 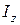 тіла відносно осі обертання (30.4.а).
тіла відносно осі обертання (30.4.а).
30.3. Фізичний маятник та його малі коливання.
Фізичним маятником називається тверде тіло, яке здійснює коливання під дією сили тяжіння навколо нерухомої горизонтальної осі обертання, яка не проходить через центр мас цього тіла.
Вісь обертання фізичного маятника  називається віссю підвісу маятника.
називається віссю підвісу маятника.
Проведемо вертикальну площину через центр мас тіла – точку С (рис. 30.2).
Нехтуючи силами тертя у підшипнику  ,запишемо диференціальне рівняння обертального коливального руху цього тіла:
,запишемо диференціальне рівняння обертального коливального руху цього тіла:
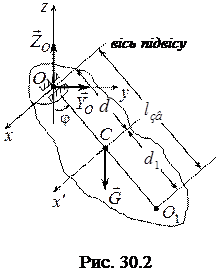
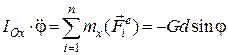 , (30.5)
, (30.5)
звідки
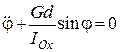 . (30.6)
. (30.6)
Обмежимося розглядом малих коливань фізичного маятника, для яких  . Тоді рівняння (30.6) набуде вигляду:
. Тоді рівняння (30.6) набуде вигляду:
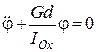
або
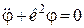 . (30.7)
. (30.7)
Тут  – квадрат частоти власних коливань маятника.
– квадрат частоти власних коливань маятника.
Як відомо, загальним розв’язком рівняння (28.7) є:
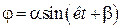 , (30.8)
, (30.8)
де 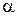 – амплітуда коливань маятника,
– амплітуда коливань маятника,  – початкова фаза коливань.
– початкова фаза коливань.
Період коливань фізичного маятника дорівнює:
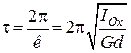 . (30.9)
. (30.9)
30.5. Експериментальне визначення моментів інерції тіл
Розглянемо визначення моментів інерції неоднорідних тіл і тіл складної конфігурації з використанням теорії фізичного маятника.
Наприклад, необхідно знайти момент інерції шатуна відносно осі, що проходить через центр тяжіння т. С (рис. 30.3). Попередньо визначимо шляхом зважування положення d – центра ваги цього шатуна (рис. 30.4):

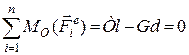 ;
; 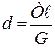 .
.
Тут  – показник динамометра.
– показник динамометра.
 |
Далі підвісимо шатун на ідеально гладкий горизонтальний циліндричний стержень і відхиливши шатун на малий кут від стану рівноваги, експериментально заміряємо період його коливань
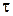 (рис. 30.3).
(рис. 30.3).
Знаючи період коливань 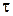 , з формули (30.9) визначаємо момент інерції шатуна відносно осі підвісу:
, з формули (30.9) визначаємо момент інерції шатуна відносно осі підвісу:
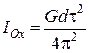 .
.
Момент інерції шатуна відносно горизонтальної осі, яка проходить через центр мас, з урахуванням, що 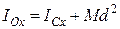 , знаходимо за формулою:
, знаходимо за формулою:
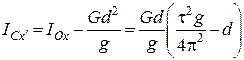 . (30.10)
. (30.10)
30.5. Диференціальні рівняння плоскопаралельного руху твердого тіла.
Вільне тверде тіло буде здійснювати плоскопаралельний рух, якщо це тіло має площину матеріальної симетрії та при цьому сили, що діють на тіло, розташовані в цій площині або у площинах, паралельних до площини матеріальної симетрії.
Рух тіла може бути плоскопаралельним і в тому випадку, якщо на нього накладено відповідні в’язі, що дозволяють тілу здійснювати вказаний рух. Але таке тіло буде вже невільним.
Якщо прийняти за полюс центр мас тіла, то диференціальні рівняння плоскопаралельного руху матимуть вигляд
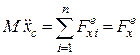 ;
; 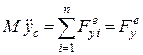 ;
;
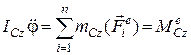 . (30.11)
. (30.11)
Перші два рівняння (30.11) описують поступальний рух твердого тіла разом із центром мас (полюсом). Третє рівняння описує обертання тіла навколо рухомої осі, яка є перпендикулярною до площини матеріальної симетрії (площини, в якій міститься центр мас тіла) і яка проходить через центр мас тіла.
30.7. Приклади розв’язання задач
 Приклад 1. Однорідний тонкий стержень довжиною
Приклад 1. Однорідний тонкий стержень довжиною 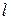 і вагою
і вагою 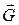 прикріплений кінцем
прикріплений кінцем 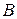 до вертикальної нитки
до вертикальної нитки 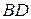 , а кінцем
, а кінцем 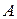 спирається на гладку горизонтальну площину, утворюючи з нею кут
спирається на гладку горизонтальну площину, утворюючи з нею кут 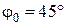 (рис. 30.5). В деякий момент часу нитку
(рис. 30.5). В деякий момент часу нитку 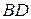 перепалюють і стержень починає падати. Визначити реакції площини в точці
перепалюють і стержень починає падати. Визначити реакції площини в точці 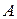 в момент початку падіння стержня.
в момент початку падіння стержня.
Розв’язання. Стержень 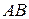 є невільним тілом. Відкинемо в’язі і замінимо їх дію на стержень силами реакцій:
є невільним тілом. Відкинемо в’язі і замінимо їх дію на стержень силами реакцій: 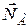 – тиск з боку площини і
– тиск з боку площини і 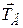 – натяг нитки. Звільнивши стержень від нитки (після її перепалювання), розглянемо його рух під дією лише двох сил
– натяг нитки. Звільнивши стержень від нитки (після її перепалювання), розглянемо його рух під дією лише двох сил 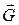 і
і  відносно системи координат Оху. Тут точка О співпадає з початковим положеннім т. А
відносно системи координат Оху. Тут точка О співпадає з початковим положеннім т. А
Покажемо штриховою лінією положення стержня 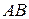 в поточний момент часу і запишемо диференціальні рівняння плоскопаралельного руху цього стержня
в поточний момент часу і запишемо диференціальні рівняння плоскопаралельного руху цього стержня
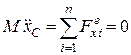 ;
; 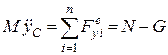 ;
;
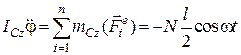 . (30.12)
. (30.12)
Інтегруємо двічі перше з рівнянь (30.19):
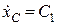 ;
; 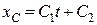 .
.
Сформулюємо початкові умови:
при 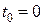 маємо
маємо 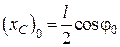 ;
; 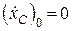 ,
,
тоді
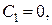
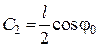 ,
,
тобто
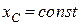 .
.
Отже, центр мас по відношенню до осі 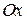 знаходиться в стані спокою, тобто центр мас пересувається лише вздовж вертикалі. Такий результат може бути отриманий з третього наслідку теореми про рух центра мас.
знаходиться в стані спокою, тобто центр мас пересувається лише вздовж вертикалі. Такий результат може бути отриманий з третього наслідку теореми про рух центра мас.
В двох останніх рівняннях (30.12) є три невідомі величини 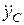 ,
,  і N. Тому для їхнього визначення треба скласти ще одне рівняння, що випливає з обмежень, які накладаються в’язями на рух стержня, тобто
і N. Тому для їхнього визначення треба скласти ще одне рівняння, що випливає з обмежень, які накладаються в’язями на рух стержня, тобто
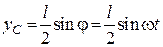 .
.
Це рівняння є законом руху центра мас стержня вздовж вертикалі. З нього маємо відповідно закони зміни швидкості та прискорення центра мас:
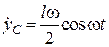 ;
;  .
.
Підставляючи отримане значення 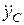 до другого рівняння системи (30.12), матимемо:
до другого рівняння системи (30.12), матимемо:
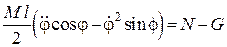 . (30.13)
. (30.13)
Підставивши значення 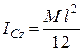 до третього рівняння системи (30.12), дістанемо
до третього рівняння системи (30.12), дістанемо
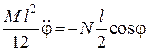
або
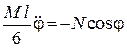 . (30.14)
. (30.14)
Домножимо рівняння (30.14) на 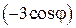 і додамо його до рівняння (30.13). Після взаємного знищення деяких доданків, отримаємо:
і додамо його до рівняння (30.13). Після взаємного знищення деяких доданків, отримаємо:
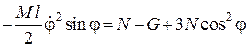 ,
,
звідки
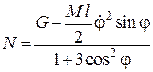 .
.
У нашому випадку при 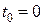 :
: 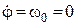 ;
; 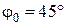 реакція
реакція 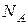 площини в точці
площини в точці 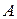 в момент початку падіння стержня має таке значення:
в момент початку падіння стержня має таке значення:
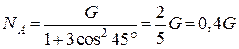 .
.
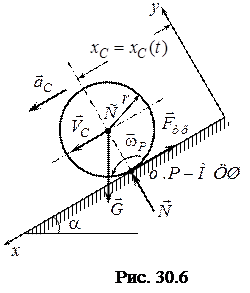 Приклад 2. Однорідний циліндр з горизонтальною віссю скочується під дією власної ваги з похилої шорсткої площини. Коефіцієнт тертя ковзання
Приклад 2. Однорідний циліндр з горизонтальною віссю скочується під дією власної ваги з похилої шорсткої площини. Коефіцієнт тертя ковзання 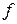 . Визначити прискорення осі циліндра, а також знайти кут нахилу
. Визначити прискорення осі циліндра, а також знайти кут нахилу 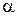 площини до горизонту, при якому циліндр котитиметься без ковзання (рис. 30.6).
площини до горизонту, при якому циліндр котитиметься без ковзання (рис. 30.6).
Розв’язання. Система диференціальних рівнянь плоскопаралельного руху циліндра має вигляд:
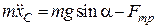 ;
;
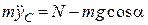 ;
;
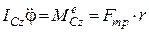 . (30.15)
. (30.15)
Оскільки циліндр котиться без ковзання, то точка Р – миттєвий центр швидкості 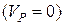 . Тому
. Тому
 ,
,
а значить
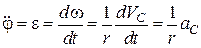 .
.
З третього рівняння системи (30.15) знаходимо  :
:
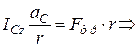
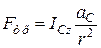 .
.
З другого рівняння системи (30.15) при 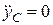 знаходимо, що
знаходимо, що 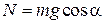 .
.
З першого рівняння системи (30.15) знаходимо 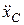 :, що дорівнює
:, що дорівнює 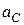 :
:
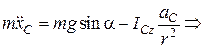
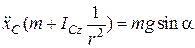 ,
,
звідки
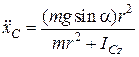 ,
, 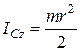 ; або
; або  .
.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 502; Нарушение авторских прав?; Мы поможем в написании вашей работы!