Тема 1. Функции нескольких переменных. Основные понятия

Действительной функцией n действительных переменных называется отображение f из R ⁿ в R (n Î N \{1}), т.е. отображение некоторого множества D (f) Ì R ⁿ на множество E (f) Ì R.

При этом D (f) называется областью определения функции f, а E (f) - множеством значений этой функции. Функцию f записывают в виде z = f (x), x = (x ₁,…, x_n) Î D (f), или подробнее, .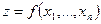

В случае, когда функция f нескольких переменных задана формулой, а ее область определения не указана, под областью определения понимается множество всех значений аргумента x, x Î R ⁿ, при которых эта формула имеет смысл во множестве R.

Графиком функции z = f (x; y) двух действительных переменных называется множество всех точек (x; y; z) Î R ³ таких, что (x; y) Î D (f), а z = f (x; y).

Линией уровня функции z = f (x; y) называется такая линия f (x; y) = C на плоскости Oxy, в точках которой функция f принимает постоянное значение z = C.

Поверхностью уровня функции u = f (x; y; z) называется такая поверхность f (x; y; z) = C пространства Oxyz, в точках которой функция f принимает постоянное значение u = C.

Пример 1. Найти и изобразить на координатной плоскости область определения следующих функций.

a) .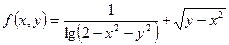

Решение. .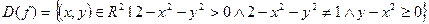

Решаем систему неравенств

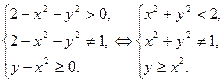
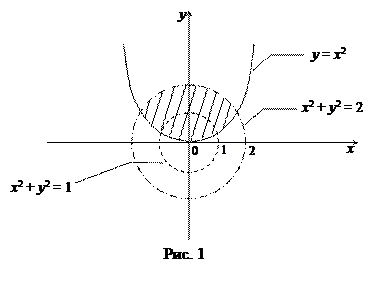Неравенство 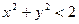задает на координатной плоскости Oxy внутренность круга с центром в начале координат и радиусом, равным 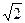, а неравенство 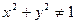- всю плоскость Oxy за исключением точек единичной окружности 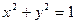. Неравенству 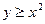соответствуют на плоскости Oxy точки параболы , а также точки, расположенные «выше» этой параболы. Множество D (f) (см. рис. 1), обозначенное штриховкой, – ограниченное несвязное множество в 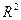, которое не является ни открытым, ни замкнутым.

б) .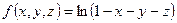

Решение. Область определения функции f представляет собой множество 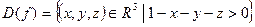. Плоскость 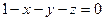делит пространство R ³ на два полупространства. Так как точка (0, 0, 0) удовлетворяет неравенству 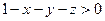, то областью определения функции f будет то из полупространств, которому принадлежит эта точка.

Пример 2. Найти множество значений E (f) функции .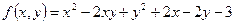

Решение. Данная функция определена для всех точек 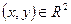. Обозначим через

.

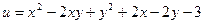(1)

Множество значений функции f есть множество значений параметра u, при которых уравнение (1) имеет хотя бы одно решение. Преобразуем уравнение (1) к виду 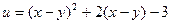. После замены 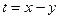, получим равносильное ему квадратное относительно t уравнение 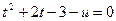. Необходимым и достаточным условием существования корней этого уравнения является неотрицательность его дискриминанта, т.е. выполнение неравенства 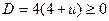. Отсюда находим .

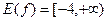Пример 3. Найти линии уровня функции .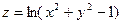

Решение. Уравнение линии уровня для данной функции имеет вид 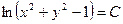, 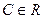. При всех действительных значениях параметра C имеем равенство

,

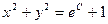задающее семейство окружностей радиуса 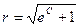центром в начале координат.

Дата добавления: 2015-04-24