Розділ 1. Поняття дійсної функції багатьох змінних

ЧАСТИНА II Диференціальне числення функцій багатьох змінних

.

Звідси слідує, що а є нерухомою точкою цього відображення.

Для доведення єдиності точки а, припустимо, що b єще одна нерухома точка відображення: b=f(b), причому a¹b. Тоді матимемо:

, бо 0< a <1.

Прийшли до суперечності. Теорему доведено.

В цьому розділі ми для функцій f, які діють з Rⁿ®R, побудуємо апарат диференційного числення і вкажемо на деякі його застосування. Оскільки областю визначення цієї функції будуть деякі множини з простору Rⁿ, кожна точка яких задається п дійсними координатами, а значеннями цієї функції є дійсні числа, то функції, які ми будемо вивчати, називатимуться дійснозначними функціями від п дійсних змінних або функціями багатьох змінних.

Таким чином, в цьому розділі ми будемо займатися функціями виду:

f: E®R¹ EÌRⁿ, E – область визначення функції, f(E)ÌR – множина значень.

Графіком функції двох дійсних змінних є деяка поверхня в просторі R³. Звичайно можна ввести поняття графіка і для функції більшої кількості змінних, але тоді ця множина М буде розміщена в просторі, розмірність якого більша або рівна 4, і цей об’єкт зобразити важко.

Із попередньої частини випливає, що для функцій багатьох змінних можна вводити поняття границі і поняття неперервності. Зауважимо, що ці речі переносяться сюди.

Домовимось, окіл точки х⁽⁰⁾, радіуса r позначати 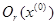, а проколотий окіл – .

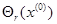Означення 1.1. (неперервність функції за Гейне). Нехай f:E®R, x⁽⁰⁾ÎE. f називається неперервною в точці х⁽⁰⁾, якщо для будь-якої послідовності { x^(к) }: x^(к)ÎE, яка збігається до х⁽⁰⁾, послідовність { f(x^(к)) } – збіжна до числа f(x⁽⁰⁾).

Означення 1.2. (неперервність функції по Коші). Нехай f: E®R, x⁽⁰⁾ÎE. Функція f називається неперервною в точці х⁽⁰⁾, якщо для будь-якого e>0 існує d>0 таке, що для всякого хÎЕ, що задовільняє нерівності r(х;x⁽⁰⁾)<d, виконується нерівність ½ f(x)-f(x⁽⁰⁾) ½<e.

Якщо х⁽⁰⁾ є граничною точкою множини Е, то означення неперервності можна сформулювати наступним чином.

Означення 1.3. Нехай f: E®R, x⁽⁰⁾ÎE і х⁽⁰⁾ гранична точка множини Е. Функція f називається неперервною в точці х⁽⁰⁾, якщо .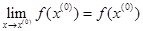

Зрозуміло, що якщо f – неперервна в усіх точках множини Е, то вона називається неперервною на множині Е.

Як і для функцій однієї змінної, так і для функцій багатьох змінних мають місце теореми Вейєрштрасса. Так, як обмежена замкнена множина в просторі Rⁿ є компактом, то на основі теореми 4.4 розділу 5, першої частини дані теореми можна сформулювати наступним чином.

Теорема 1.1. (Теорема Вейєрштрасса). Якщо функція f неперервна на обмеженій і замкненій множині FÌRⁿ, то вона обмежена на цій множині і досягає на ній своїх найбільшого і найменшого значень.

Теорема 1.2. Якщо G відкрита і зв’язна множина в просторі Rⁿ, то будь-які дві точки цієї множини можна з’єднати неперервною кривою, всі точки якої належать множині G.

Доведення. Припустимо, що висновок теореми не вірний. Це означає, що існують дві точки х ⁽¹⁾і х ⁽²⁾, які належать множині G, які не можна з’єднати неперервною кривою, всі точки якої належать множині G.

Позначимо через А множину, що містить точку х ⁽¹⁾ і всі ті точки множини G, які можна з’єднати із точкою х ⁽¹⁾ неперервною кривою, яка належить G. Решту точок, - позначимо через В. Тобто В=G – A.

Оскільки G – відкрита, то х ⁽¹⁾ входить в G разом з деяким своїм околом. Зрозуміло, що всі точки околу можна з’єднати з центром неперервною кривою (навіть прямолінійним відрізком), тобто до А входять всі точки з околу. Це означає, що А – непорожня і відкрита множина, бо якщо якась точка х⁽³⁾ Î А, тобто її можна з¢єднати з х ⁽¹⁾ неперервною кривою, то неперервною кривою можна з’єднати з точкою х ⁽¹⁾ всі точки з деякого околу точки х ⁽³⁾.

Очевидно, що В – непорожня (бо там є х⁽²⁾) і також відкрита. Із побудови видно, що А Ç В=Æ, а також, що G= A È B. Оскільки множина G зв’язна, то хоча б одна з цих множин містить точку дотику другої. Нехай точка х⁽⁰⁾ Î А є точкою дотику множини В. Тоді в будь-якому околі точки х⁽⁰⁾ є хоча б одна точка з множини В. Візьмемо окіл точки х⁽⁰⁾, який міститься в G. Всі точки з цього околу можна сполучити з х⁽⁰⁾ неперервною кривою, яка лежить в G, а значить х⁽⁰⁾ не може бути точкою дотику множини В. Аналогічно встановлюється, що жодна точка множини В не може бути точкою дотику множини А. Прийшли до суперечності. Теорему доведено.

Приклад. Нехай маємо функцію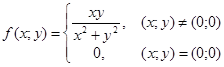

Чи буде функція неперервною в точці (0;0)? Для цього потрібно з’ясувати чи буде ?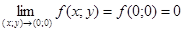

За умовою . Розглянемо два шляхи прямування (x;y)®(0;0).

,

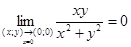, а це означає, що дана функція в даній точці границі не має. Значить в цій точці функція має розрив.

Нагадаємо, що будь-яка зв’язна відкрита множина, називаєтся областю.

Множина, що є об’єднанням області G і її граничних точок, називається замкненою областю.

Теорема1.3. (про неперервність складної функції). Нехай маємо функцію z=f(x ₁, x₂,…, x_n) причому точка (х₁,...,х_п)ÎЕ, EÌRⁿ. Нехай задано ще таку систему функцій:

х ₁ =j ₁ (t ₁ ,…,t_k)

x₂=j₂(t ₁ ,…t_k)

.....................

x_n=j_n(t ₁ ,…,t_k),

де точки (t ₁ ,…,t_k)ÎGÌR^k. Якщо функції j ₁ ,…,j_n неперервні в точці С=(t ₁ ⁽⁰⁾,…,t_k⁽⁰⁾)ÎG, а функція z=f(x ₁, x₂,…, x_n) неперервна в точці (х ₁ ⁽⁰⁾,…х_п⁽⁰⁾)=х⁽⁰⁾ÎЕ (тут х ₁ ⁽⁰⁾=j ₁ (t ₁ ⁽⁰⁾,…,t_k⁽⁰⁾), х₂⁽⁰⁾=j₂(t ₁ ⁽⁰⁾,…,t_k⁽⁰⁾),..., х_п⁽⁰⁾=j_п(t ₁ ⁽⁰⁾,…,t_k⁽⁰⁾)), то складна функція z від (t ₁ ,…,t_k) – неперервна в точці t⁽⁰⁾= =(t ₁ ⁽⁰⁾,…,t_k⁽⁰⁾).

Доведення. Оскільки функції j ₁ ,...,j_п – неперервні в точці t⁽⁰⁾, то (з означення неперервності за Гейне), для будь-якої послідовності { t^{(і )}}, яка належить множині G і збіжна до t⁽⁰⁾ матимемо, що х^(і)=(х ₁ ^(і),...,х_п^(і))® (х ₁ ⁽⁰⁾,…х_п⁽⁰⁾). Тоді, оскільки функція f(x ₁, x₂,.., x_n)= f(x) є неперервною в точці х⁽⁰⁾, то за означенням Гейне, з того, що послідовність {х^(і)} збігається до х⁽⁰⁾, слідує, що , або те саме,

Дата добавления: 2015-05-24