Билет 5. Радиосигналы с амплитудной модуляцией и его параметры. Спектр АМ-сигнала. Ширина спектра

Если переменной оказывается амплитуда сигнала U(t), причём остальные два параметра 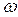и 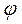неизменны, то имеется амплитудная модуляция (АМ) несущего колебания. Форма записи АМ-сигнала, такова:

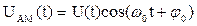(5.2)

В соответствии с формулой (5.2) АМ-сигнал есть произведение огибающей U(t) и гармонического заполнения 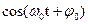. В большинстве практических случаев огибающая изменяется во времени гораздо медленнее, чем высокочастотное заполнение.

При АМ связь между огибающей U(t) и модулирующим полезным сигналом S(t) определяется следующим образом:

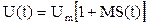(5.3)

Здесь постоянный коэффициент, равный амплитуде несущего колебания в отсутствие модуляции; М – коэффициент АМ. Величина М – характеризует глубину АМ.

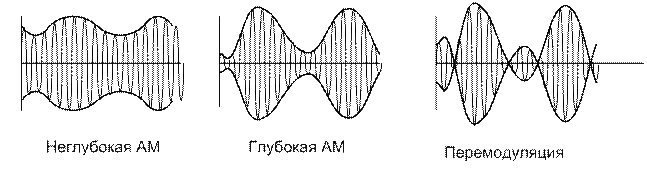При малой глубине модуляции относительное изменение огибающей невелико, то есть 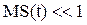во все моменты времени независимо от формы сигнала S(t).

Если же в момент времени, когда сигнал S(t) достигает экстремальных значений, имеются приближённые равенства.

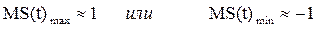то говорят о глубокой АМ.

АМ-сигналы с малой глубиной модуляции нецелесообразны ввиду неполного использования мощности передатчика. В то же время 100%-ная модуляция (М=1) в два раза повышает амплитуду колебаний при пиковых значениях модулированного сообщения. Дальнейший рост этой амплитуды, как правило, приводит к нежелательным искажениям из-за перегрузки выходных каскадов передатчика.

Не менее опасна слишком глубокая АМ (при М>1) называемая перемодуляцией. Здесь форма огибающей перестаёт повторять форму модулированного сигнала.

Однотональная АМ.

Простейший АМ-сигнал может быть получен в случае, когда модулирующим низкочастотным сигналом является гармоническое колебание с частотой Такой сигнал

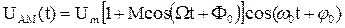(5.4)

называется однотональным АМ-сигналом. Такой сигнал можно представить как сумму простых гармонических колебаний с различными частотами. Используя известную тригонометрическую формулу произведения косинусов, из выражения (5.4) сразу получаем:

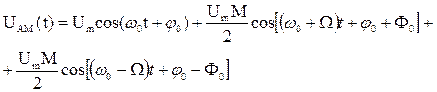(5.5)

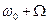Формула (5.5) устанавливает спектральный состав однотонального АМ-сигнала. Принята следующая терминология: - несущая частота, - верхняя боковая частота, 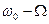нижняя боковая частота.

Строя по формуле (5.5) спектральную диаграмму однотонального АМ-сигнала, следует обратить внимание на равенство амплитуд верхнего и нижнего боковых колебаний, а также на симметрию расположения этих спектральных составляющих относительно несущего колебания.

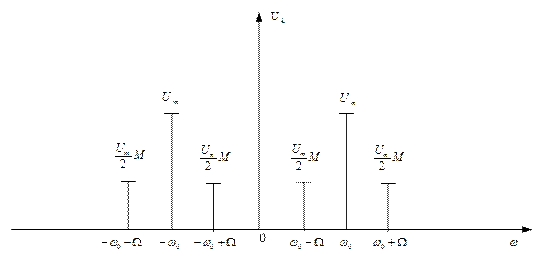
Если рассмотреть вопрос о соотношении мощностей несущего и боковых колебаний, то путём несложных математических преобразований можно убедиться, что средняя мощность АМ-сигнала равна сумме средних мощностей несущего и боковых колебаний.

(5.6)

Откуда следует:

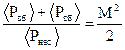(5.7)

Даже при 100%-ной модуляции (М=1) доля мощности обоих боковых колебаний составляет лишь 50% от мощности немодулированного несущего колебания.

А поскольку информация о сообщении заключена в боковых колебаниях, можно сделать вывод о неэффективности использования мощности при передаче АМ-сигнала.

АМ при сложном модулирующем сигнале

На практике однотональные АМ-сигналы используются редко. Гораздо более реален случай, когда модулирующий низкочастотный сигнал имеет сложный спектральный состав. Математической моделью такого сигнала может быть, например, тригонометрическая сумма.

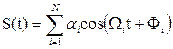(5.8)

Здесь частоты 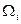образуют упорядоченную возрастающую последовательность 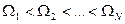, В то время как амплитуды 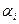и начальные фазы 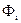произвольны.

Подставив формулу (5.8) в (5.3), получим:

(5.9)

Введём совокупность парциальных (частичных) коэффициентов модуляции: и запишем аналитическое выражение сложномодулированного сигнала (многотонального) АМ-сигнала в форме, которая обобщает выражение (5.4)

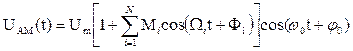(5.11)

Спектральное разложение проводится так же, как и однотонального АМ-сигнала:

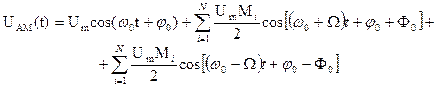(5.12)

На рисунке а) изображена спектральная диаграмма модулирующего сигнала S(t), построенная в соответствии с формулой (5.8). Рисунок б) воспроизводит диаграмму многотонального АМ-сигнала, где помимо несущего колебания, содержатся группы верхних и нижних боковых колебаний. С целью упрощения изображены только физические спектры.

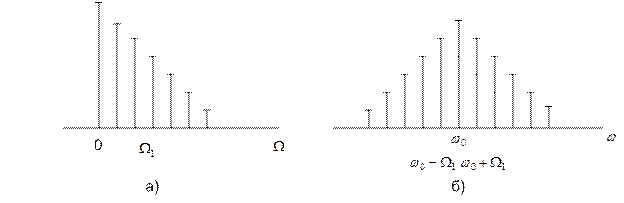Спектр верхних боковых колебаний является масштабной копией спектра модулированного сигнала, сдвинутой в область высоких частот на величину 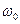. Спектр нижних боковых колебаний так же повторяет спектральную диаграмму сигнала S(t), но располагается зеркально относительно несущей частоты 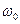. Отсюда следует важный вывод: ширина спектра АМ-сигнала равна удвоенному значению наивысшей частоты в спектре модулирующего низкочастотного сигнала.

Амплитудно-манипулированные сигналы.

Важным классом многотональных АМ-сигналов являются так называемые манипулированные сигналы. В простейшем случае это – последовательности радиоимпульсов, отделённых друг от друга паузами. Такие сигналы широко используются в технике связи. Если S(t) – функция, в каждый момент времени принимающая значение либо 0, либо1, то амплитудно-манипулированный сигнал представляется в виде:

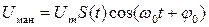(5.14)

Пусть, например, функция S(t) отображает периодическую последовательность видеоимпульсов. Считая, что амплитуда этих импульсов A=1, на основании (5.14) имеем при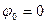

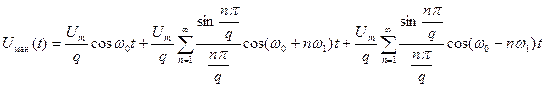(5.15)

Где q - скважность последовательности (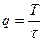, 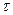– длительность одного импульса).

Балансная АМ.

Как видно из предыдущего, значительная доля мощности АМ – сигнала сосредоточена в несущем колебании. Для более эффективного использования мощности передатчика можно формировать АМ – сигналы с подавленным несущим колебанием, реализуя так называемую балансную АМ(БМ). На основании формулы (5.4) представление однотонального АМ – сигнала с БМ таково:

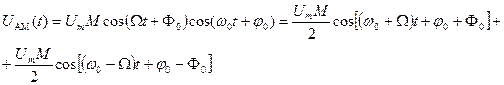(5.16)

Имеет место перемножение двух сигналов – модулирующего и несущего. Колебания вида (5.16) с физической точки зрения являются биениями двух гармонических сигналов с одинаковыми амплитудами 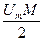и частотами, равными верхней и нижней боковым частотам.

При многотональной БМ аналитическое выражение сигнала принимает вид:

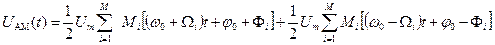(5.17)

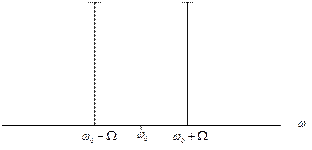
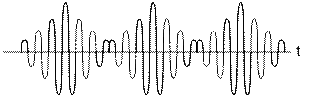
Рассмотрим спектральную и временную диаграмму БМ – сигнала.

Как и при обычной АМ, в спектре БМ наблюдается две симметричные группы верхних и нижних боковых колебаний.

Если рассмотреть временную диаграмму биений, может показаться неясным, почему в спектре этого сигнала нет несущей частоты, хотя налицо присутствие высокочастотного заполнения, изменяющегося во времени именно с этой частотой.

Дело в том, что при переходе огибающей биений через нуль фаза высокочастотного заполнения скачком изменяется на 180 градусов, поскольку функция имеет разные знаки слева и справа от нуля. Если такой сигнал подать на высокодобротную колебательную систему (например,LС-контур), настроенную на частоту 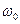, то выходной эффект будет очень мал, стремясь к нулю при возрастании добротности. Колебания в системе, возбуждённые одним периодом биений, будут гаситься последующим периодом.

Однополосная амплитудная модуляция.

Ещё более интересное усовершенствование принципа обычной АМ заключается в формировании сигнала с подавленной верхней или нижней боковой полосой частот (ОБП).

Сигналы с одной боковой полосой (SSB - singl side band) по внешним характеристикам напоминают обычные АМ-сигналы. Например, однотональный ОБП-сигнал с подавленной нижней боковой частотой записывается в виде:

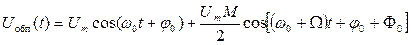(5.18)

Проводя тригонометрические преобразования, получаем:

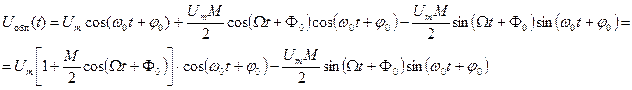
(5.19)

Два последних слагаемых представляют собой произведение двух функций, одна из которых изменяется во времени медленно, а другая – быстро.

Основное преимущество ОБП-сигналов – двукратное сокращение полосы занимаемых частот, что оказывается существенным для частотного уплотнения каналов связи.

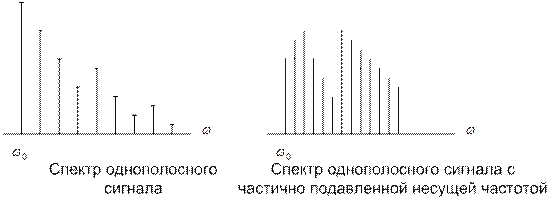
Дальнейшим усовершенствованием систем ОБП является частичное или полное подавление несущего колебания. При этом мощность передатчика используется ещё более эффективно.

Билет 18. Воздействие гармонического колебания на резистивный элемент при степенной аппроксимации. Воздействие гармонических колебаний на резистивный элемент при кусочно-линейной аппроксимации. Коэффициенты Берга. Бигармоническое воздействие на нелинейный элемент при степенной аппроксимации.

В соответствии с определением данного метода, расчет нелинейной цепи с его использованием включает в себя в общем случае следующие основные этапы:

1. Исходная характеристика нелинейного элемента заменяется ломаной линией с конечным числом прямолинейных отрезков.

2. Для каждого участка ломаной определяются эквивалентные линейные параметры нелинейного элемента и рисуются соответствующие линейные схемы замещения исходной цепи.

3. Решается линейная задача для каждого отрезка в отдельности.

4. На основании граничных условий определяются временные интервалы движения изображающей точки по каждому прямолинейному участку (границы существования отдельных решений).

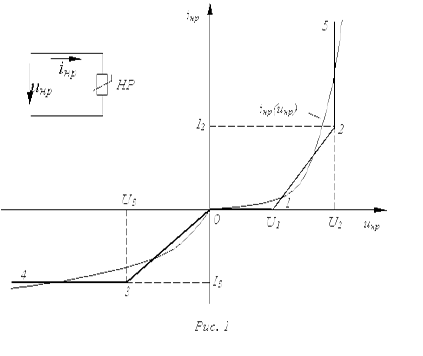
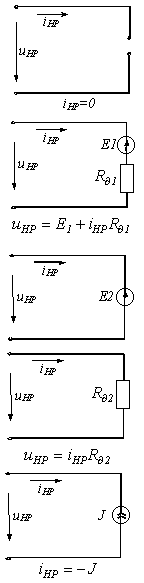
Пусть вольт-амперная харак-теристика (ВАХ) нелинейного резистора имеет форму, представленную на рис. 1. Заменяя ее ломаной линией 4-3-0-1-2-5, получаем приведенные в табл. 1 расчетные эквивалентные схемы замещения и соответ-ствующие им линейные соотношения.

Расчет каждой из полученных линейных схем замещения при наличии в цепи одного нелинейного элемента и произвольного числа

линейных не представляет труда. В этом случае на основании теоремы об активном двухполюснике исходная нелинейная цепь сначала сводится к схеме, содержащей эквивалентный генератор с некоторым линейным внутренним сопротивлением и последовательно с ним включенный нелинейный элемент, после чего производится ее расчет. При наличии в цепи переменного источника энергии рабочая (изображающая) точка будет постоянно скользить по аппроксимирующей характеристике, переходя через точки излома. Переход через такие точки соответствует мгновенному изменению схемы замещения. Поэтому задача определения искомой переменной сводится не только к расчету схем замещения, но и к определению моментов “переключения” между ними, т.е. нахождению граничных условий по времени. Анализ существенно усложняется, если в цепи имеется несколько нелинейных элементов. Главная трудность в этом случае связана с тем, что заранее не известно сочетание линейных участков, соответствующее заданному входному напряжению (току). Искомое сочетание линейных участков всех нелинейных элементов определяется перебором их возможных сочетаний. Для любого принятого сочетания параметры схемы известны, и, следовательно, могут быть определены напряжения и токи для всех элементов. Если они лежат в пределах соответствующих линейных участков, то принятое сочетание дает верный результат. Если хотя бы у одного нелинейного элемента переменные выходят за границы рассматриваемого линейного участка, то следует перейти

Таблица 1. Кусочно-линейная аппроксимация ВАХ нелинейного резистора

Участок аппроксимирующей кривой	Схема замещения	Параметры элементов	Граничные условия
0 - 1 1 - 2 2 - 5 3 - 0 2 - 5

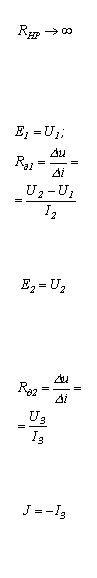
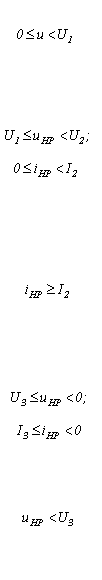
к другому сочетанию. Необходимо отметить, что всегда имеется единственное сочетание линейных участков характеристик нелинейных элементов, соответствующее изменению входного сигнала в некоторых пределах.

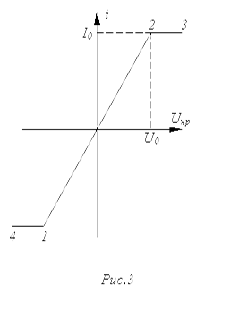
В качестве примера определим напряжение в цепи на рис. 2, в которой 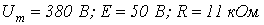. ВАХ нелинейного резистора приведена на рис. 3, где .

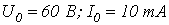Решение

1. В соответствии с заданной ВАХ нелинейный резистор на участке 1-2 заменяем линейным резистором с сопротивлением

,

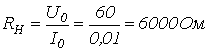на участке 2-3-источником тока с током 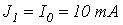и на участке 4-1-источником тока с током .

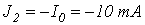2. На основании данной эквивалентной замены для тока на участке 1-2 ВАХ можно записать:

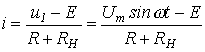
(1)

откуда

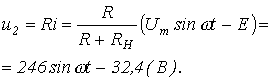
При движении изображающей точки по участку 2-3 ВАХ имеем

,

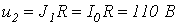при движении по участку 1-4 ВАХ-

.

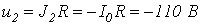3. Определяем интервалы движения изображающей точки по отдельным участкам ВАХ. Для точки излома 1 на основании (1) справедливо уравнение

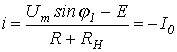
или

.

Отсюда получаем два значения мгновенной фазы питающего напряжения на одном периоде, соответствующих точке 1: . Первое значение определяет переход изображающей точки с участка 4-1 на участок 1-2, второе – с участка 2-1 на участок 1-4.

Аналогично записываем для точки 2 излома ВАХ

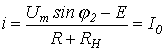
или

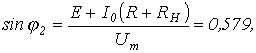
откуда 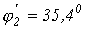(значение, соответствующее переходу с участка 1-2 на участок 2-3) и 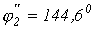(значение, соответствующее переходу с участка 3-2 на участок 2-1).

Таким образом, получаем для одного периода питающего напряжения

;

;

;

;

.

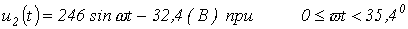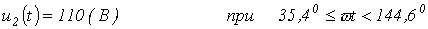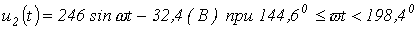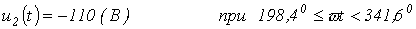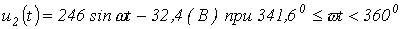
В соответствии с периодичностью синусоидальной функции данные решения повторяются через 360°n.

На рис. 4 представлен график зависимости искомой величины.

Дата добавления: 2015-05-09