Расчет устойчивости откосов

При проектировании котлованов и траншей глубиной более 5 м необходимо произвести расчет устойчивости откосов.

Большинство существующих методов расчета устойчивости откосов основывается на рассмотрении предельного равновесия грунта, при котором даже незначительное изменение объемных или поверхностных сил приводит к его потере.

Откос, образованный несвязным сыпу­чим грунтом, будет находиться в равнове­сии, если в равновесии находится каждый элемент его поверхности.

На выделенный элемент М (рис. 9) при уровне грунтовых вод ниже основания от­коса действует сила Я — его вес, которую заменяем нормалью давления N и каса­тельной к поверхности откоса силой сдви­га Т.

:

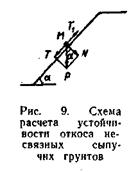
Условия предельного равновесия на данной площадке можно выразить равенством

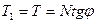
где φ — угол внутреннего трения грунта.

Из рис. 9 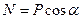, a .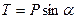

Подставляя в формулу предельного равновесия значения N н Т, получим

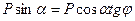
Поделив обе части равенства на 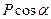, получим: 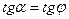, или 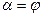. Следовательно, в сыпучих грунтах предельный угол откоса равен углу внутреннего трения грунта. Для сыпучих тел этот угол называется углом естественного откоса. Откос будет устойчив, если угол, образованный его поверхностью с горизон­том, не превышает угла внутреннего трения грунта. Устойчи­вость откоса в несвязных сыпучих грунтах не зависит от его высоты. Всякий откос с углом наклона больше q> является неус­тойчивым.

Если уровень грунтовых вод поднимется выше основания от­коса (например, после ливневого дождя), то на величину угла естественного откоса будет влиять гидродинамическое давление D фильтрующейся через откос воды, направленное по касатель­ной к линии потока. Максимальный угол, при котором частицы грунта будут находиться в покое при подъеме грунтовых вод, можно опре­делить графически (рис. 10).

Выделим условно на поверхности откоса объем грунта, равный едини­це. На выделенный элемент грунта кроме собственного веса Р (который следует принимать с учетом взвеши­вающего действия воды) действует гидродинамическое давление D.

Результирующее давление R опре­деляется путем построения параллело­грамма сил Р и D.

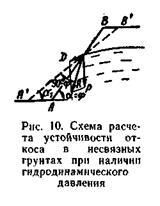
От направления равнодействующей откладываем угол, равный 90° — φ, по­лученное направление А'В' определит предельный угол откоса α₁ с учетом влияния грунтовой воды.

Условия устойчивости откоса в грунтах, обладающих трени­ем и сцеплением, оказываются весьма сложными, даже если принять, что массив грунта однороден, а сопротивление его сдви­гу независимо от времени.

Условия предельного равновесия грунта, обладающего тре­нием и сцеплением на данной площадке, в общем виде можно выразить равенством

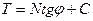
Исследование состояния предельного равновесия грунта ве­лось в двух направлениях:

создании упрощенной схемы предельного равновесия, позво­ляющей путем принятия ряда допущений решать задачи об устойчивости земляных масс простейшими способами;

создании строгой теории предельного равновесия, позволяю­щей решать задачи устойчивости земляных масс, не вводя огра­ничений в формы и положения линий скольжения. К первому направлению относятся методы расчета откосов, предложенные Терцаги, Н. Н. Масловым, А. И. Ивановым и др. Ко второму на­правлению относится теория предельного состояния сыпучей среды В. В. Соколовского. В дальнейшем С. С. Голушкевич раз­работал графический метод решения задач, в котором рассмат­ривал откос, находящийся в состоянии предельного равновесия, а А. М. Сенков упростил метод расчета В. В. Соколовского.

В целях облегчения отыскания опасной линии скольжения ряд исследователей для решения этой задачи предложили раз­личные таблицы и графики.

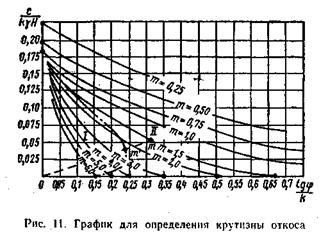
Например, Б. М. Ломизе построил график (рис. 11), позво­ляющий решать следующие задачи:

определять допустимую высоту откоса Н, если известны γ, φ, С и К и крутизна откоса 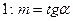, где m — коэффициент отко­са, равный отношению заложения к высоте откоса;

определять требуемую крутизну откоса 1:m, если известны γ, φ, С, Н и m;

определять коэффициент устойчивости К, если известно γ, φ, С, Н и m.

График (рис. 11) позволяет решать все основные задачи, воз­никающие при расчете устойчивости плоских откосов в однород­ных грунтах. Каждая кривая графика соответствует определен­ному значению m начиная от m = 0,25 до m = 6. Причем если расчетные данные находятся в области I графика, то опасная поверхность скольжения выклинивается в основании за преде­лами откоса, а если в области II, то опасная поверхность сколь­жения проходит через точку пересечения откоса с основанием. Граница между областями показана на графике рисунка штрих-пунктиром. При 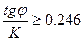опасная поверхность скольжения всегда проходит через точку пересечения откоса с основанием. Вы­клинивание опасных поверхностей скольжения за пределами от­коса может иметь место только при очень малых значениях угла внутреннего трения.

Приближенное определение координат точек, лежащих на поверхности устойчивого откоса, предложили И. С. Мухин

Таблица 14.

φ = 5^0	φ =10^0	φ =15°	φ = 20°	φ = 25°	φ = 30°	φ = 35°	φ = 40°
z	у	z	у	z	и	z	У	z	V	z	V	z	у	z	У
0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00
0,25	0,01	0,25	0,01	0,30	0,01	0,30	0,01	0,50	0,02	0,51	0,02	0,56	0,02	0,51	0,01
0,50	0,05	0,51	0,04	0,56	0,04	1,04	0,12	1,04	0,10	1,05	0,08	1.16	0,08	1,04	0,05
1,04	0,22	1,02	0,17	1,03	0,14	2,03	0,45	2,28	0,46	2,01	0,29	2,19	0,28	2,01	0,19
1,99	0,85	2,01	0,68	1,98	0,53	3,17	1,06	3,00	0,77	3,03	0,64	3,42	0,65'	3,04	0,42
3,07	2,28	2,95	1,50	3,04	1,24	4,23	1,84	4,12	1,40	4,19	1,16	4,77	1.19	4,21	0,76
3,95	4,30	4,18	3,11	4,00	2,12	5,49	2,99	5,18	2,13	5,3	1,78	5,94	1,75	5,34	1,17
4,99	8,15	5,17	4,94	5,09	3,38	7,08	4,81	6,32	3,04	6,49	2,55	7,19	2,45	6,55	1,07
5,96	12,90	6,13	7,15	5,97	4,64	8,80	7,14	7,52	4,16	7,76	3,49	8,54	3,30	7,84	2,29
6,46	15,60	7,11	9,77	7,33	6,92	10,00	9,00	8,80	5,49	9,12	4,62	9,99	4,31	9,24	3,03
—	—	8,13	12,80	8,27	8,72	12,00	12,30	10,20	7,05	10,60	5,96	11,60	5,50	10,70	3,90
—	—	9,22	16,13	9,27	10,8	Н,30	16,40	11,60	8,87	12,20	7,51	13,30	6,90	12,30	4,92

и А. И. Срагович. Составленные ими таблицы для облегчения вычислений координат приведены в сокращенном виде (табл. 14).

Пример 1. Построить кривую равнопрочного откоса для назначения кру­тизны откоса выемки в суглинистом грунте при следующих данных: высота откоса Н=10м; γ =1.95т/м³; φ = 17°; С=1,9 г/м².

Первый вариант решения — построение кривой равнопрочного откоса по теории предельного равновесия проф. В. В. Соколовского с использованием графиков и упрощений проф. А. М. Сенкова.

Ординаты точек кривой равнопрочного откоса вычисляем по формуле

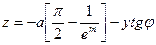
где ,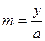

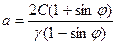
Проф. А. М. Сенков член 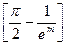обозначил через ζ, тогда

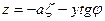
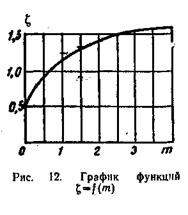
Для определения числового значения ζ построен график функций ζ = f(m), приведенный на рис. 12.

Для нашего примера находим показатель а:

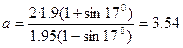
Задаваясь различными значениями у, определяем 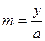. Результаты подсчетов сводим в табл. 15. По полученным значениям координат у и z строим кривую 1 равнопрочного откоса (рис. 13).

Второй вариант решения — построение кривой равнопрочного откоса по приближенному методу проф. Н. Н. Маслова, известного под названием, ме­тода равнопрочного откоса. Этот метод основывается на двух основных пред­посылках: угол устойчивого откоса для любой горной породы есть угол ее сопротивления сдвигу (ψ_р); критическое напряжение в толще определяется

Таблица 15

у,м	а		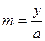ς по графику (рис. 12)	а ς	tgφ	у tg φ	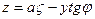м
	3,54	0)282,	0,80	2,83	0,31	0,31	-3,14
	3,54	0,564	1,00	3,54	0,31	0,61	-4,15
	3,54	1,13	1,25	4,42	0,31	1,22	-5,64
	3,54	1,69	1,35	4,72	0,31	1,84	-6,56
	3,54	2,26	1,47	5,21	0,31	2,45	-7,66
	3,54	2,82	1,50	5,31	0,31	3,06	-8,37
	3,54	3,38	1,53	5,41	0,31	3,67	-9,08
	3,54	3,95	1,55	5,49	0,31	4,28	-9,77
	3,54	6,77	1,55	5,49	0,31	7,35	-12,84

равенством двух главных напряжений, равных весу столба грунта высотой, равной глубине погружений точки от горизонтальной поверхности грунта. Коэффициент сдвига Fp является тангенсом угла сдвига Ψр_z, т.е.

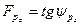или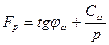

р — вертикальная равномерно распределенная нагрузка от сооружения в кГ/см² (р=γz);

φ_ω — угол внутреннего трения грунта в град;

С_ω — сила сцепления грунта в кГ/см² или Т/м².

При построении кривой равнопрочного откоса ординатой z задаются и определяют угол наклона отрезка поверхности откоса к горизонту α_z, равный углу сдвига Ψр_z, т. е. α_z= Ψр_z.

Вычисляют величину α_z при z = 0; 1; 2; 4; 6; 8; 10. Для каждого значе­ния z определяют величину α_z при разной нагрузке р=γz. Подсчитывают

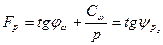
Подставляя числовые значения, вычисляют величину устойчивого угла от­коса и результаты сводят в табл. 16.

Таблица 16

z, м	γ, т/м^3	p = γz т/м^2	tgφω	Сω,т/м^2		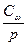Fp=tgφω+
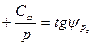
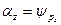
	1,95	1,95	0,31	1,9	0,975	1,285	52°
	1,95	3,90	0,31	1,9	0,488	0,798	38,5°
	1,95	7,80	0,31	1.9	0,244	0,554	29°
	1,95	11,70	0,31	1,9	0,162	0,472	25,5°
	1,95	15,60	0,31	1,9	0,120	0,430	23,5°
	1,95	19,50	0,31	1,9	0,097	0,410	22,5°
	1,95	23,40	0,31	1,9	0,081	0,391	21,5°
	1,95	27,30	0,31	1.9	0,070	0,380	21,0°

Полученные значения а, откладываем на рис. 13, начиная построение снизу вверх.

Из рис. 13 видно, что приближенный метод Fp почти совпадает с теоре­тически строгим методом В. В. Соколовского.

Пример. 2. Определить допустимую крутизну откоса 1: т:

1) в глинистом грунте, если известны: H=6 м; γ = 195 т/м³ φ=17°- С = 1,9 Т/м²; К=1,25.

Пользуясь методом Б. М. Ломизе (см. рис. 11), находим значения

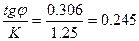и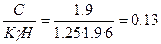

отвечающие условиям предельного равновесия откоса. По графику (см. рис. 11) находим: m=0,5: 1:m = tga=2, откуда а=63°30';

2) в песчаном грунте, если известны: Н=6 м; γ =1,8 т/м³; φ=30°; С=0,2 Т/м²; К=1,25:

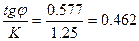и

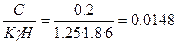
По графику (см. рис. II) находим m=l,7; I: m = tga = 0,538; a = =30°30'.

Пример. 3. Определить крути­зну откоса выемки глубиной H = 10 м при наличии нагрузки на его поверхности Р=2Т/м² грунт глинистый γ=1.95т/м³; φ=17°; С =1,9 Т/м².

Воспользуемся приближенным аналитическим методом равнопрочного от­коса (метод Fр), предложенным проф. Н. Н. Масловым:

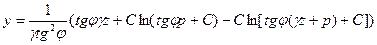
Определяем значения постоянных членов формулы:

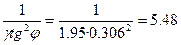м³/Т

Т/м²

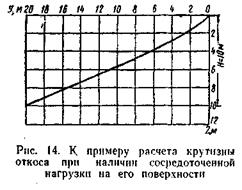
Принимаем z = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 м и для этих значении вычисляем переменные члены формулы. Результаты вычислений сводим в табя. 17. По данным табл. 17 строим кривую равнопрочного откоса (рис.14).

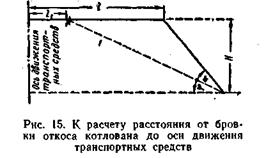
Пример 4. Определить расстояние l от бровки откоса котлована до оси движения транспортных средств (рис. 15) при следующих данных: глубина котлована Н = 4м; грунт — супесь, φ=25°; угол рабочего откоса 50⁰ (φ+α); l₁ = 2м.

В типовых технологических картах на производство земляных работ механизированным способом, разработанных государственным институтом Проектгидромеханизация (Госстройиздат, 1963) для определения расстояния от бровки откоса котлована до оси движения транспортных средстй, рекомендо­вана следующая формула:

где l₁ — расстояние от оси пути до пересечения с линией, образуемой естественным откосом грунта, в м,

Н — глубина котлована в м;

φ — угол естественного откоса в град;

а— угол между гранью рабочего откоса и гранью естественного откоса (α=50—25=25°).

Таблица 17

z, м	γ^z	tgφγz	1.75+ tgφγz	γz+p	tgφ(γz+p)	tgφ(γz+p)+C	C ln [tgφ(γz+p)+C]	Разность данных гр.4 и 8	5,48 умножить на зн. гр.9
	1,95	0,597	2,35	3,95	1,205	3,105	2,05	0,30	1,64
	3,90	1,19	2,94	5,90	1,805	3,703	2,31	0,63	3,4t
	5,85	1,79	3,54	7,85	2,400	4,300	2,76	0,78	4,26
	7,80	2,39	4,14	9,80	3,000	4,900	3,01	1,13	6,20
	9,75	2,98	4,73	11,75	3,600	5,500	3,22	1,51	8,30
	11,70	3,58	5,33	13,70	4,200	6,100	3,42	1,91	10,45
	13,65	4,17	5,92	15,65	4,800	6,700	3,60	2,32	12,70
	15,60	4,78	6,53	17,60	5,380	7,280	3,75	2,78	15,25
	17,55	5,37	7,14	19,55	6,000	7,900	3,90	3,24	17,75
	19,50	5,97	7,72	21,50	6,600	8,500	4,05	3,67	20,10

Подставляя в формулу числовые значения, получи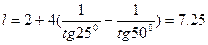м:

м

Дата добавления: 2015-06-28