
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Множини міри нуль і вимірні функції 1 страница
|
|
|
|
Вступ
Анотація.
Побудова простору Лебега
МП
Руководитель
Рекомендации для совершенствования профессиональной деятельности работника
III. Оценка профессиональных компетенций и продуктивности деятельности
аттестуемого работника*
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Информационная компетентность аттестуемого работника (владение информационными, мультимедийными технологиями и цифровыми ресурсами)_________________________________
Выводы и предложения для аттестационной комиссии Министерства образования и науки Республики Татарстан:
______________________________________________________соответствует (не соответствует)
(Должность, фамилия, имя, отчество аттестуемого работника)
занимаемой должности
1.
2.
образовательного учреждения __________________ (расшифровка подписи)
(подпись)
С представлением ознакомлен(а)_____________20_____г. ______________ ( расшифровка подписи)
(подпись)
*Объем информации в пункте III «Оценка профессиональных компетенций и результативности деятельности аттестуемого работника» не ограничивается форматом данного образца представления. В соответствии с п. 20 Порядка аттестации, представление должно содержать мотивированную, всестороннюю и объективную оценку профессиональных деловых качеств и компетенций на основе квалификационной характеристики по занимаемой должности; сведений о результативности работы за период, предшествующий аттестации работника. Общий объем представления не должен превышать 4 л.
|
|
|
Описание профессиональных компетенций педагогических работников и разъяснения по их оценке опубликованы на сайте МО и Н РТ (mon.tatar.ru) в разделе «Педагогическая аттестация»/ Нормативные документы/Методика оценки квалификации педагогических работников
Курсова робота
Науковий керівник:
доцент Фотій О.Г.
Виконав:
Студент 305 групи
Плантус І.І.
Чернівці 2015
Дана курсова робота присвячена детальному розбору четвертого розділу «Теорія інтегралу» з [1].
Зміст
Вступ …………………………………………………………………………4
§1 Множини міри нуль і вимірні множини……....................................5
§2 Клас С+....................................................................................................10
§3 Сумовні функції та простір Лебега ……………………………….…17
Література…………………………………………………………………...25
Класичне визначення інтегралу, дане Коші і Ріманом є цілком достатнім для застосування до окремих неперервних або кусково-неперервних функцій, але для більш широкого класу функцій цього визначення недостатньо. Відомо [2, с. 93], що простір 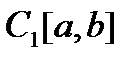 неперервних функцій
неперервних функцій 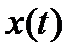 на відрізку
на відрізку 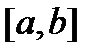 з метрикою
з метрикою 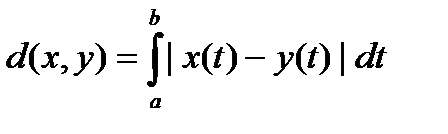 не є повним, і приєднання до простору розривних функцій інтегровних за Ріманом нічого не змінює. Тільки нова конструкція інтегралу, більш ширша, ніж Ріманова, дозволяє вказати клас функції, що дає поповнення простору по вище згаданій метриці.
не є повним, і приєднання до простору розривних функцій інтегровних за Ріманом нічого не змінює. Тільки нова конструкція інтегралу, більш ширша, ніж Ріманова, дозволяє вказати клас функції, що дає поповнення простору по вище згаданій метриці.
Нагадаємо [3, c. 125], що коли 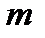 - міра, задана на півкільці
- міра, задана на півкільці 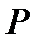 в
в 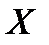 ,
, 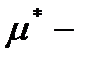 зовнішня міра в
зовнішня міра в 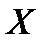 , що породжена мірою,
, що породжена мірою, 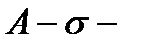 алгебра
алгебра 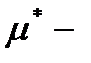 вимірних множин в
вимірних множин в 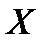 , які ми надалі будемо називати просто вимірними, і
, які ми надалі будемо називати просто вимірними, і 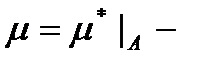 стан-дартне продовження міри
стан-дартне продовження міри 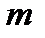 з напівкільця
з напівкільця 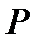 на
на 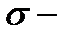 алгебру
алгебру 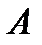 .
.
Ті підмножини 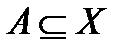 називається множиною міри нуль. Рівність
називається множиною міри нуль. Рівність 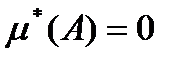 означає, що для кожного
означає, що для кожного 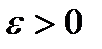 існує така послідовність елементів
існує така послідовність елементів 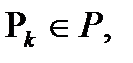 що
що 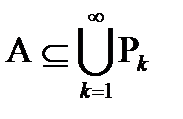 i
i 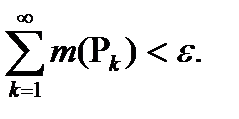
Якщо множина А є підмножиною відрізку 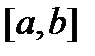 , то означення множини міри нуль буде виглядати так: A називається множиною міри нуль, якщо для довільного
, то означення множини міри нуль буде виглядати так: A називається множиною міри нуль, якщо для довільного 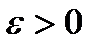 її можна покрити скінченною або зліченною послідовністю інтервалів, сума довжин яких не перевищує
її можна покрити скінченною або зліченною послідовністю інтервалів, сума довжин яких не перевищує 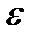 .
.
|
|
|
Твердження 1.1. Довільна зліченна сукупність точок є множиною міри нуль. Довільний відрізок [a,b] не є множиною нуль.
Доведення. Нехай 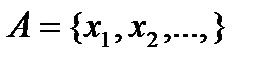 - зліченна множина. Зафіксуємо деяке
- зліченна множина. Зафіксуємо деяке 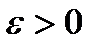 . Тоді послідовність інтервалів з довжинами
. Тоді послідовність інтервалів з довжинами 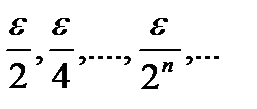 покриває точки
покриває точки 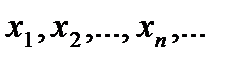 множини А і має загальну суму довжин, не більше ніж
множини А і має загальну суму довжин, не більше ніж 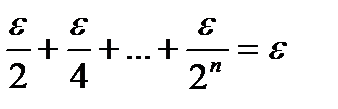 . Отже, множина А є множиною міри нуль.
. Отже, множина А є множиною міри нуль.
Доведемо тепер, що відрізок 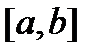 не є множиною нуль. Справді, якщо відрізок покритий системою відкритих інтервалів числової прямої, то за лемою Гейне-Бореля [2, c. 122], можна з даного покриття вибрати скінченне підпокриття; сума довжин навіть цих інтервалів перевищує число
не є множиною нуль. Справді, якщо відрізок покритий системою відкритих інтервалів числової прямої, то за лемою Гейне-Бореля [2, c. 122], можна з даного покриття вибрати скінченне підпокриття; сума довжин навіть цих інтервалів перевищує число 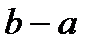 , тобто довжину всього відрізка
, тобто довжину всього відрізка 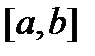 .
.
Множини міри нуль є такими, що значення функції на цій множині не є суттєвим при обчисленні інтегралу від неї.
Твердження 1.2. Інтеграл від функції 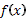 , який рівний одиниці на множині А міри нуль, і рівний нулю на доповненні А, рівний нулю.
, який рівний одиниці на множині А міри нуль, і рівний нулю на доповненні А, рівний нулю.
Доведення. Покриємо множину А системою інтервалів з загальною довжиною меншою за 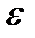 . Зрозуміло, що інтеграл від функції
. Зрозуміло, що інтеграл від функції 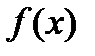 , якщо він визначений правильно, не повинен перевищувати суму площ прямокутників висотою 1 та основами на вказаних інтервалах. А ця сума рівна сумі довжин самих інтервалів і за умовою менша
, якщо він визначений правильно, не повинен перевищувати суму площ прямокутників висотою 1 та основами на вказаних інтервалах. А ця сума рівна сумі довжин самих інтервалів і за умовою менша 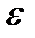 , тобто може бути як завгодно малою. Звідси, необхідно випливає, що функція
, тобто може бути як завгодно малою. Звідси, необхідно випливає, що функція 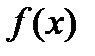 повинна мати інтеграл, рівний нулеві.
повинна мати інтеграл, рівний нулеві.
Зауважимо, що в наведеному означенні множини міри нуль можна замінити покриття множини інтервалами, покриттям із відрізків або будь-яких проміжків (із включеними чи невключеними кінцями). Справді, якщо є покриття множини А проміжками з загальною довжиною меншою 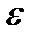 , то, замінюючи n -ий проміжок з інтервалом довжини, не більше нiж на
, то, замінюючи n -ий проміжок з інтервалом довжини, не більше нiж на 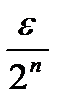 перевищуючи довжину n -го проміжку, отримаємо і покриття множини А інтервалами, загальна довжина яких не перевищує тому, якщо множину А можна покрити системою якихось проміжків з загальною довжиною як завгодно малою, то можна покрити і системою інтервалів з загальною довжиною також як завгодно малою, тобто множина А має міру нуль.
перевищуючи довжину n -го проміжку, отримаємо і покриття множини А інтервалами, загальна довжина яких не перевищує тому, якщо множину А можна покрити системою якихось проміжків з загальною довжиною як завгодно малою, то можна покрити і системою інтервалів з загальною довжиною також як завгодно малою, тобто множина А має міру нуль.
Вкажемо просту конструкцію замкнутих множин міри нуль. Припустимо, що замкнута множина F на відрізку 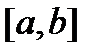 отримується викиданням із цього відрізка відкритої множини, яка складається із скінченої сукупності неперетинних інтервалів
отримується викиданням із цього відрізка відкритої множини, яка складається із скінченої сукупності неперетинних інтервалів 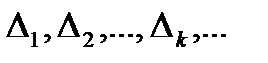 з загальною довжиною, рівною
з загальною довжиною, рівною 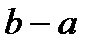 . Тоді ми можемо стверджувати, що множина F має міру нуль. Справді, для заданого
. Тоді ми можемо стверджувати, що множина F має міру нуль. Справді, для заданого 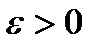 , можна знайти таке n, що
, можна знайти таке n, що
|
|
|
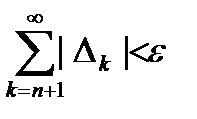 .
.
Через 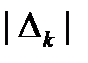 ми, тут і надалі, позначатимемо довжину інтервалу
ми, тут і надалі, позначатимемо довжину інтервалу  . Ті n інтервалів, котрі залишилися не перетинаються і разом з проміжками відрізками
. Ті n інтервалів, котрі залишилися не перетинаються і разом з проміжками відрізками 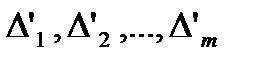 (число яких m може бути рівне
(число яких m може бути рівне 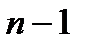 , n або
, n або 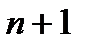 , виключаючи той випадок, коли
, виключаючи той випадок, коли 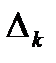 i
i 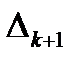 мають спільний кінець і, отже,
мають спільний кінець і, отже, 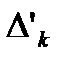 вироджується в точку) дають скінченне покриття (проміжками) всього відрізку
вироджується в точку) дають скінченне покриття (проміжками) всього відрізку 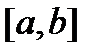 . Так як сума довжин
. Так як сума довжин 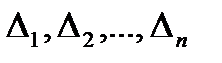 більша, ніж
більша, ніж 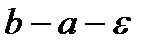 , то система
, то система 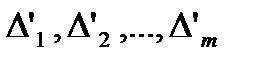 має загальну довжину меншу за
має загальну довжину меншу за 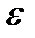 ; а так як вона, очевидно, покриває всю множину F, то ми і отримаємо, що F є множиною міри нуль.
; а так як вона, очевидно, покриває всю множину F, то ми і отримаємо, що F є множиною міри нуль.
Здавалось би, важко очікувати, що після викидання із відрізку довжиною 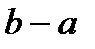 системи неперервних інтервалів з загальною довжиною також
системи неперервних інтервалів з загальною довжиною також 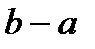 може залишитися як завгодно багата точками множина. Виявляється, що тим не менше залишок може бути навіть еквівалентний (за потужністю) всьому вихідному відрізку.
може залишитися як завгодно багата точками множина. Виявляється, що тим не менше залишок може бути навіть еквівалентний (за потужністю) всьому вихідному відрізку.
Прикладом може бути канторова множина на відрізку 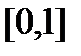 [3, с. 124].
[3, с. 124].
Приклад 1. Канторова множина С визначається так. Відрізок 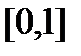 ділиться на три рівних частини точками
ділиться на три рівних частини точками 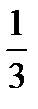 і
і 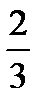 , і середній інтервал
, і середній інтервал 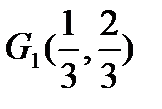 викидається. Дві відрізки
викидається. Дві відрізки 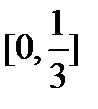 i
i 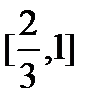 знову діляться на три рівних частини відповідно точками
знову діляться на три рівних частини відповідно точками 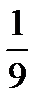 і
і 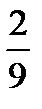 та
та 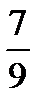 і
і 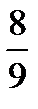 , і об’єднання
, і об’єднання 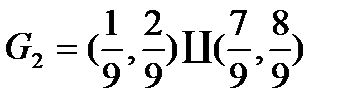 знову викидається. Те ж саме пророблюється з чотирма відрізками
знову викидається. Те ж саме пророблюється з чотирма відрізками 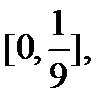
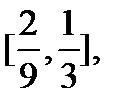
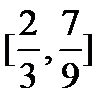 i
i 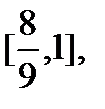 що залишилися, потім з вісьмома відрізками, що залишилися, і цей процес продовжується до нескінченності. Те, що з відрізка
що залишилися, потім з вісьмома відрізками, що залишилися, і цей процес продовжується до нескінченності. Те, що з відрізка 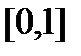 при цьому залишиться при такому викиданні – це і є канторова множина С.
при цьому залишиться при такому викиданні – це і є канторова множина С.
Позначимо символом 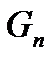 множину, яка викидається на n -му кроці. Це відкрита множина, яка має
множину, яка викидається на n -му кроці. Це відкрита множина, яка має 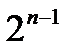 складових інтервалів
складових інтервалів 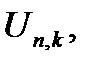 кожний з яких має довжину
кожний з яких має довжину 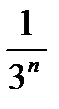 . Тому
. Тому 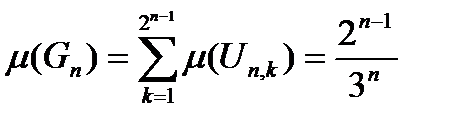 . Зрозуміло, що множини
. Зрозуміло, що множини 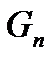 попарно не перетинаються, тому для їх об’єднання
попарно не перетинаються, тому для їх об’єднання 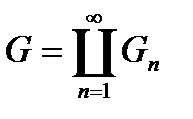 будемо мати
будемо мати 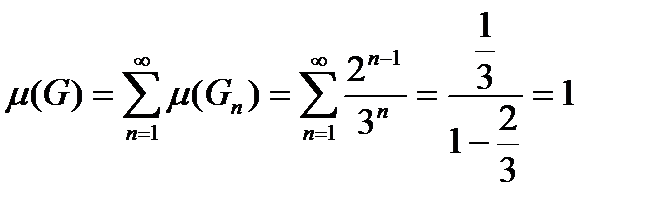 . Різниця
. Різниця 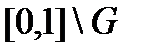 і є за означенням канторова множина С, яка є замкненою, адже G відкрита. Тому множина С вимірна за Лебеґом і
і є за означенням канторова множина С, яка є замкненою, адже G відкрита. Тому множина С вимірна за Лебеґом і 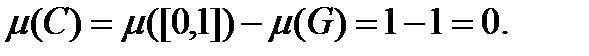
Можна показати, що множина С складається з тих і тільки тих 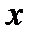 з відрізка
з відрізка 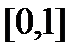 , які допускають зображення у вигляді трійкового дробу
, які допускають зображення у вигляді трійкового дробу 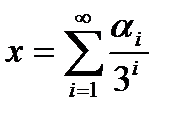 , де
, де 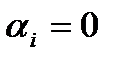 або 2. Звідси легко вивести, що потужність канторової множини, як і всього відрізка
або 2. Звідси легко вивести, що потужність канторової множини, як і всього відрізка 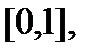 дорівнює потужності континуума с. Таким чином, на прямій і континуальні множини можуть мати нульову міру.
дорівнює потужності континуума с. Таким чином, на прямій і континуальні множини можуть мати нульову міру.
|
|
|
Тому згідно вище сказаному канторова множина має міру нуль. Надалі ми часто будемо використовувати наступну властивість множини міри нуль.
Лема 1. Об’єднання скінченної або зліченної сукупності множин міри нуль є множиною міри нуль.
Доведення. Розглянемо одразу випадок зліченної сукупності 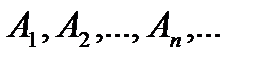 множин міри нуль. Для заданого
множин міри нуль. Для заданого 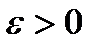 і для кожного
і для кожного 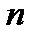 покриємо множину
покриємо множину 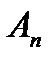 зліченною системою інтервалів з загальною довжиною менше
зліченною системою інтервалів з загальною довжиною менше 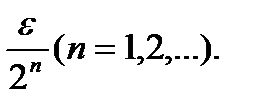 Тоді вся множина
Тоді вся множина 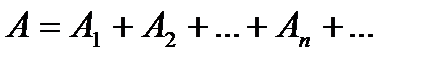 виявиться покритою зліченною системою інтервалів (сума зліченної множини зліченних множин) з загальною довжиною, меншою за
виявиться покритою зліченною системою інтервалів (сума зліченної множини зліченних множин) з загальною довжиною, меншою за 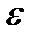 . Тому,
. Тому, 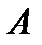 має міру нуль, що і потрібно було довести. Якщо деякою властивістю володіють всі точки відрізка
має міру нуль, що і потрібно було довести. Якщо деякою властивістю володіють всі точки відрізка 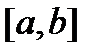 , за можливим виключенням множини міри нуль, то ми кажемо, що вона виконана “майже для всіх точок” або “на множині повної міри”.
, за можливим виключенням множини міри нуль, то ми кажемо, що вона виконана “майже для всіх точок” або “на множині повної міри”.
Наприклад, майже для всіх точок 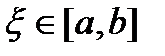 , виконується та властивість, що
, виконується та властивість, що 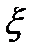 ірраціональне. Бувають функції майже скрізь неперервні, тобто неперервні в кожній точці, крім, можливо, множини міри нуль. Для функцій, яким дозволяється приймати і нескінченні значення, має зміст назва “скінченна майже скрізь”; це означає, що множиною, на якій функція нескінченна, сама більша є множина міри нуль. Тепер ми можемо описати клас функцій, в якому буде проходити наша подальша робота по визначенню інтегралу. Функції, котрі входять в цей клас, називаються вимірними функціями.
ірраціональне. Бувають функції майже скрізь неперервні, тобто неперервні в кожній точці, крім, можливо, множини міри нуль. Для функцій, яким дозволяється приймати і нескінченні значення, має зміст назва “скінченна майже скрізь”; це означає, що множиною, на якій функція нескінченна, сама більша є множина міри нуль. Тепер ми можемо описати клас функцій, в якому буде проходити наша подальша робота по визначенню інтегралу. Функції, котрі входять в цей клас, називаються вимірними функціями.
Східчастою функцією є функція, яка приймає деяке стале значення в кожному із інтервалів деякого розбиття відрізка 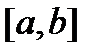 на частини за допомогою точок поділу
на частини за допомогою точок поділу 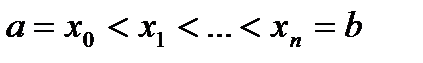 .
.
В самих точках поділу ми можемо не цікавитися значеннями східчастої функції, оскільки цих точок скінченна кількість – і тим самим множина міри нуль. Сукупність східчастих функцій є лінійним простором із звичайними операціями додавання і множення на числа: якщо 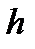 i
i 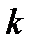 – східчасті функції, то їх лінійна комбінація
– східчасті функції, то їх лінійна комбінація 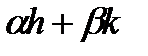 також є східчастою функцією.
також є східчастою функцією.
Вимірною функцією є така функція, яка визначена і скінченна майже скрізь на відрізку 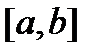 і може бути представлена як границя майже скрізь збіжної послідовності східчастих функцій.
і може бути представлена як границя майже скрізь збіжної послідовності східчастих функцій.
Твердження 1.3. Вимірні функції утворюють лінійний простір.
Доведення. Нехай східчасті функції 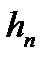 збігаються до функції
збігаються до функції 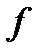 скрізь, крім множини
скрізь, крім множини 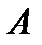 міри нуль, а східчасті функції
міри нуль, а східчасті функції 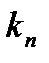 – до функції
– до функції 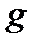 скрізь, крім множини
скрізь, крім множини 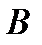 міри нуль, то східчасті функції
міри нуль, то східчасті функції 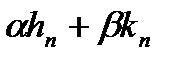 збігаються до функції
збігаються до функції 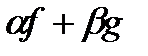 скрізь, крім множини
скрізь, крім множини 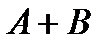 , яка, за доведеною лемою 1, також є множиною міри нуль; отже, функція
, яка, за доведеною лемою 1, також є множиною міри нуль; отже, функція 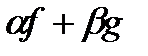 також вимірна. І багато інших властивостей, якими володіє клас східчастих функцій, можна подібним граничним переходом перенести на клас вимірних функцій.
також вимірна. І багато інших властивостей, якими володіє клас східчастих функцій, можна подібним граничним переходом перенести на клас вимірних функцій.
Твердження 1.4. Нехай 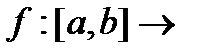
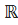 і
і 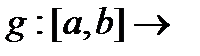
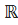 - вимірні функції і
- вимірні функції і 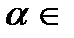
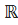 . Тоді функції
. Тоді функції 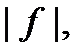
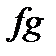 ,
, 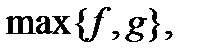
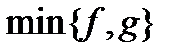 визначенні на множині
визначенні на множині 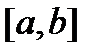 і є вимірними. Частка
і є вимірними. Частка 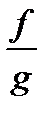 визначена на множині
визначена на множині 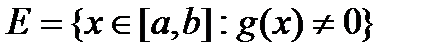 і є там вимірною.
і є там вимірною.
Взагалі кажучи, разом з функцією 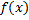 вимірними являються її додатня і від’ємна частина
вимірними являються її додатня і від’ємна частина 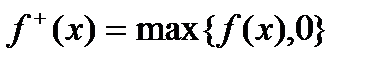 і
і 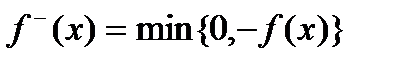 .
.
§2. Клас С+
Приступимо до побудови поняття інтегралу.
Розглянемо спершу східчасту функцію 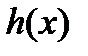 , тобто функцію, яка приймає сталі значення
, тобто функцію, яка приймає сталі значення 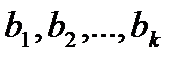 в кожного із скінченного числа проміжків
в кожного із скінченного числа проміжків 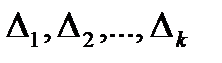 , на які відрізок
, на які відрізок 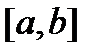 розбивається точками поділу
розбивається точками поділу 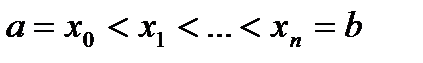 .
.
Інтеграл від східчастої функції природно визначити так:
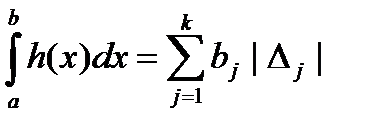 .
.
Для скорочення запису надалі будемо вираз вигляду 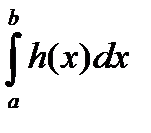 позначимо через
позначимо через 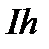
Теорема 2.1. Інтеграл від східчастих функцій володіє наступними властивостями:
і) 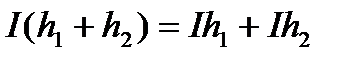 для будь-яких двох східчастих функцій
для будь-яких двох східчастих функцій 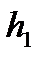 i
i 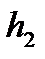 ;
;
іі) 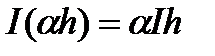 для будь-якого числа
для будь-якого числа 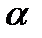 ;
;
ііі) якщо 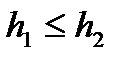 , то
, то 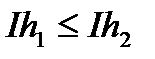 ; взагалі кажучи, якщо
; взагалі кажучи, якщо 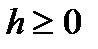 то
то 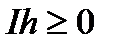 ;
;
iv) якщо послідовність 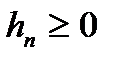 монотонно спадає (так, що
монотонно спадає (так, що 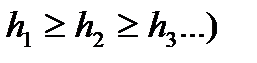 і прямує до нуля майже скрізь, то
і прямує до нуля майже скрізь, то 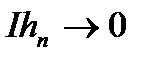 ;
;
v) якщо послідовність 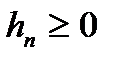 монотонно спадає і при цьому
монотонно спадає і при цьому 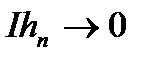 то ця послідовність прямує до нуля майже скрізь.
то ця послідовність прямує до нуля майже скрізь.
Надалі для позначення граничного переходу при монотонному спаданні будемо використовувати знак 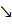 , так що, наприклад, запис
, так що, наприклад, запис 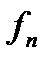
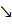
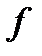 означає, що послідовність функцій
означає, що послідовність функцій 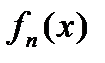 , монотонно спадаючи, прямує майже скрізь до функції
, монотонно спадаючи, прямує майже скрізь до функції 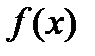 . Аналогічно
. Аналогічно 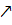 :
: 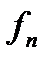
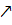
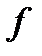 означає, що послідовність функцій
означає, що послідовність функцій 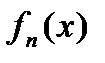 , монотонно зростаючи, прямує майже скрізь до функції
, монотонно зростаючи, прямує майже скрізь до функції 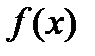 .
.
Доведемо властивість iv). Нехай, що 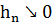 і доведемо що
і доведемо що 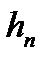
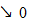 . Класичну теорему про почленне інтегрування збіжної послідовності функцій тут застосовувати неможна, оскільки ця теорема передбачає рівномірну збіжність послідовності функцій до своєї границі. Для доведення поступимо наступним чином. Об’єднання множини, на якій послідовність
. Класичну теорему про почленне інтегрування збіжної послідовності функцій тут застосовувати неможна, оскільки ця теорема передбачає рівномірну збіжність послідовності функцій до своєї границі. Для доведення поступимо наступним чином. Об’єднання множини, на якій послідовність 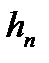 не збігається до нуля, і зліченної множини точок розриву всіх
не збігається до нуля, і зліченної множини точок розриву всіх 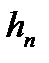 позначимо через
позначимо через 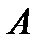 ; це – множина міри нуль. Покриємо її системою інтервалів
; це – множина міри нуль. Покриємо її системою інтервалів 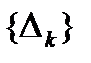 з загальною довжиною, меншою заданого
з загальною довжиною, меншою заданого 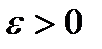 . Кожній із залишившихся точок
. Кожній із залишившихся точок 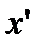 спів ставимо номер
спів ставимо номер 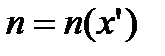 , для якого виконується нерівність
, для якого виконується нерівність 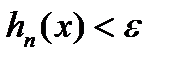 , та інтервал
, та інтервал 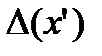 що містить цю точку, в якому функція
що містить цю точку, в якому функція 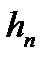 зберігає своє значення. Інтеграли
зберігає своє значення. Інтеграли 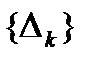 разом з інтервалами
разом з інтервалами 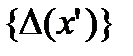 утворюють покриття відрізка
утворюють покриття відрізка 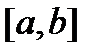 , із якого ми можемо вибрати скінченне під покриття. Позначимо ці інтервали через
, із якого ми можемо вибрати скінченне під покриття. Позначимо ці інтервали через 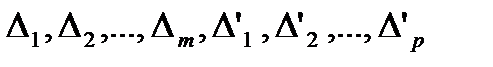 , позначаючи штрихом ті інтервали, які побудовані за точками
, позначаючи штрихом ті інтервали, які побудовані за точками 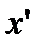 . Якщо
. Якщо 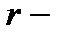 найбільший із номерів, які відповідають відповідним точкам
найбільший із номерів, які відповідають відповідним точкам 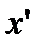 , то функція
, то функція 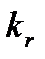 та наступні функції на інтервалах
та наступні функції на інтервалах 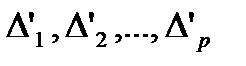 не перевищують
не перевищують 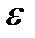 . На інтервалах
. На інтервалах 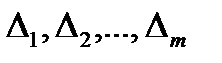 , сума довжин яких, за побудовою, менша
, сума довжин яких, за побудовою, менша 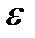 , ці функції не перевищують числа
, ці функції не перевищують числа 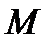 максимума функції
максимума функції 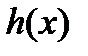 . Тепер зрозуміло, що для інтегралу від функції
. Тепер зрозуміло, що для інтегралу від функції 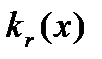 по відрізку
по відрізку 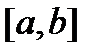 і для інтегралу для всіх наступних функцій ми отримаємо оцінку вигляду
і для інтегралу для всіх наступних функцій ми отримаємо оцінку вигляду 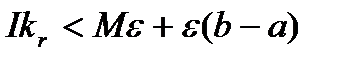 . Так як
. Так як 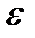 можна було взяти довільно малим, то ми приходимо до висновку, що
можна було взяти довільно малим, то ми приходимо до висновку, що 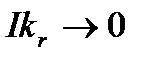 , що і потрібно було довести.
, що і потрібно було довести.
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 1918; Нарушение авторских прав?; Мы поможем в написании вашей работы!