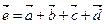КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Скалярное, векторное и смешанное произведения векторов
|
|
|
|
Прямоугольная (декартова) система координат
Векторы. Линейные операции над векторами
Глава II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Определение 1. Вектором называется направленный отрезок 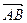 с начальной точкой А и конечной точкой В. Вектор, начало и конец которого совпадают, называется нулевым вектором и обозначается
с начальной точкой А и конечной точкой В. Вектор, начало и конец которого совпадают, называется нулевым вектором и обозначается 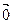 . Вектор
. Вектор 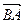 называется вектором, противоположным вектору
называется вектором, противоположным вектору 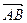 .
.
Определение 2. Длиной 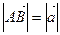 вектора
вектора 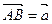 называется число, равное длине отрезка АВ, соединяющего точки А и В. Вектор, длина которого равна единице, называется единичным вектором или ортом.
называется число, равное длине отрезка АВ, соединяющего точки А и В. Вектор, длина которого равна единице, называется единичным вектором или ортом.
Определение 3. Два вектораназываются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Векторы в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Определение 4. Два коллинеарных вектораназываются одинаково (противоположно) направленными, если их концы лежат по одну сторону (по разные стороны) от прямой, соединяющей их начала, или от общего начала.
Определение 5. Два вектораназываются равными, если они имеют одинаковые длины и одинаково направлены. Все нулевые векторы считаются равными.
Здесь 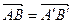 .
.
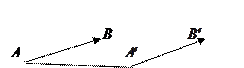
Определение 6. Произведением вектора  на число αили числа α на вектор
на число αили числа α на вектор 
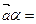
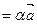 называется вектор, длина которого равна
называется вектор, длина которого равна 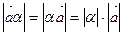 , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора  , если α > 0, или противоположно направлению вектора
, если α > 0, или противоположно направлению вектора  , если α < 0.
, если α < 0.
Сумма двух векторов находится по правилу треугольника или по правилу параллелограмма.
Определение 7 (правило треугольника). Суммой векторов  и
и  называется вектор
называется вектор 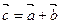 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец – с концом вектора
, а конец – с концом вектора  , расположенного таким образом, что его начало совпадает с концом вектора
, расположенного таким образом, что его начало совпадает с концом вектора  .
.
|
|
|
Определение 8 (правило параллелограмма). Суммой векторов 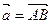 и
и 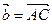 называется вектор
называется вектор 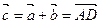 , являющийся диагональю параллелограмма,
, являющийся диагональю параллелограмма,
построенного на векторах  и
и  как на сторонах.
как на сторонах.
|





 Вычитание векторов – операция, обратная операции сложения.
Вычитание векторов – операция, обратная операции сложения.
| 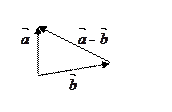 | |||
Определение 9. Разностью векторов  и
и  называется такой вектор
называется такой вектор 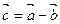 , при сложении которого с вектором
, при сложении которого с вектором  получается вектор
получается вектор  .
.
|




Прямую, на которой указано направление, будем называть направленной прямой.
Определение 1. Углом между векторами  и
и  называется угол между соответствующими сторонами параллелограмма, построенного на векторах
называется угол между соответствующими сторонами параллелограмма, построенного на векторах  и
и  как на сторонах. Углом между вектором
как на сторонах. Углом между вектором  и направленной прямой L называется угол между вектором
и направленной прямой L называется угол между вектором и любым вектором, направление которого совпадает с направлением прямой L.
и любым вектором, направление которого совпадает с направлением прямой L.
Определение 2. Числовой проекцией вектора  на направленную прямую L называется произведение длины вектора
на направленную прямую L называется произведение длины вектора  на косинус угла между вектором
на косинус угла между вектором  и прямой L: пр
и прямой L: пр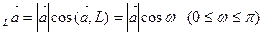 .
.
Числовые проекции векторов  и
и  на направленную прямую L имеют следующие свойства:
на направленную прямую L имеют следующие свойства:
пр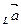 + пр
+ пр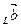 = пр
= пр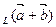 , (2.1)
, (2.1)
пр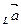 - пр
- пр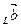 = пр
= пр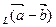 , (2.2)
, (2.2)
пр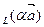 = α пр
= α пр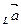 . (2.3)
. (2.3)
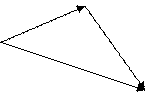
Справедливость формулы (2.1) видна, например, из следующего рисунка:
 | |||
 |
 пр
пр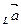 = АВ, пр
= АВ, пр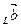 = ВС,
= ВС,

 пр
пр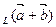 = АС.
= АС.
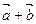 Формулы (2.2) и (2.3) получаются
Формулы (2.2) и (2.3) получаются
 аналогично.
аналогично.
L
А В С
Введем теперь понятие координат вектора. Для этого рассмотрим прямоугольную (декартову) систему координат на плоскости.
Определение 3. Прямоугольной (декартовой) системой координат на плоскости называются две взаимно перпендикулярные направленные прямые (оси координат), проходящие через точку О (начало координат), на которых выбраны единичные отрезки. Одна из осей (Ох) называется осью абсцисс, другая (Оу) – осью ординат. Оси координат делят плоскость на четыре равные области – четверти или квадранты.
|
|
|
Определение 4. Координатами вектора  называются числовые проекции вектора
называются числовые проекции вектора  на оси координат.
на оси координат.
Если х и у – координаты вектора  , то будем писать
, то будем писать  = (х, у).
= (х, у).
Пусть 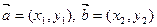 . В силу формул (2.1) – (2.3) имеем
. В силу формул (2.1) – (2.3) имеем 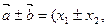
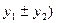 ,
,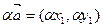 , т.е. над координатами векторов производятся те же операции (умножение на число, сложение и вычитание), что и над векторами.
, т.е. над координатами векторов производятся те же операции (умножение на число, сложение и вычитание), что и над векторами.
Аналогично определяются координаты вектора в пространстве с помощью прямоугольной (декартовой) системы координат в пространстве.
Определение 5. Прямоугольной (декартовой) системой координат в пространстве называются три взаимно перпендикулярные направленные прямые (оси координат), проходящие через точку О (начало координат). Оси координат называются осью абсцисс, осью ординат и осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями. Они делят пространство на 8 областей – октантов.
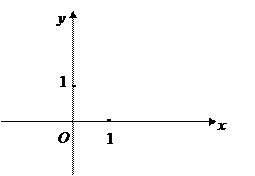 |  | ||
Прямоугольная (декартова) система координат названа в честь Рене Декарта (1596-1650) – французского математика (Турень), жившего много лет в Голландии и умершего в Стокгольме, куда он был приглашен шведской королевой. Заслуга Декарта состоит прежде всего в том, что он последовательно применил хорошо развитую алгебру начала семнадцатого века к геометрическому анализу древних и таким образом расширил область ее применимости. Основной труд – «Геометрия» (1637 г.).
С помощью прямоугольных (декартовых) координат на плоскости и в пространстве определяются координаты точек на плоскости и в пространстве.
Определение 6. Пусть А – произвольная точка трехмерного пространства, в котором задана прямоугольная (декартова) система координат. Вектор 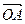 называется радиус-вектором точки А, а его координаты – координатами точки А.
называется радиус-вектором точки А, а его координаты – координатами точки А.
Таким образом, в трехмерном пространстве каждая точка имеет три координаты - абсциссу х, ординату у и аппликату z: А (х, у, z).
Аналогично определяются координаты точки А на плоскости: А (х, у). Их две – абсцисса х и ордината у.
Рассмотрим теперь более сложные – нелинейные – операции над векторами: скалярное, векторное и смешанное произведения векторов.
|
|
|
Определение 1. Скалярным произведением двух векторов  и
и  называется число
называется число  , равное произведению длин этих векторов и косинуса угла между ними:
, равное произведению длин этих векторов и косинуса угла между ними:
 =
= 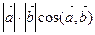 . (3.1)
. (3.1)
Поскольку 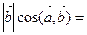 пр
пр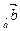 , а
, а 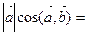 пр
пр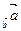 (см. определение 2 §2), получаем, что
(см. определение 2 §2), получаем, что  =
= 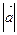 пр
пр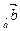 =
= 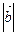 пр
пр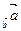 .
.
Свойства скалярного произведения:
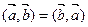 , (3.2)
, (3.2)
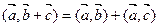 , (3.3)
, (3.3)
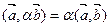 . (3.4)
. (3.4)
Равенство (3.2) вытекает из определения скалярного произведения:  =
= 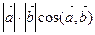 =
=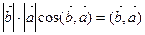 .
.
Равенства (3.3) и (3.4) доказываются с помощью формул (2.1) и (2.3):
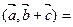
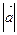 пр
пр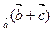 =
= 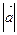 пр
пр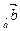 +
+ 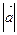 пр
пр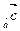 =
= 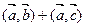 ,
,
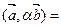
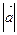 пр
пр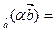
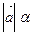 пр
пр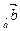 =
= 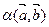 .
.
Из (3.2) и (3.3) имеем
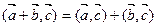 , (3.5)
, (3.5)
так как 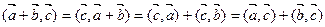 , а из (3.2) и (3.4):
, а из (3.2) и (3.4):
 , (3.6)
, (3.6)
поскольку 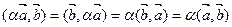 .
.
Для того, чтобы записать скалярное произведение в координатной форме, обозначим через 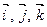 единичные векторы координатных осей Ох, Оу, Оz в пространстве соответственно. Очевидно, что
единичные векторы координатных осей Ох, Оу, Оz в пространстве соответственно. Очевидно, что 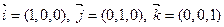 . Поэтому
. Поэтому 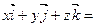
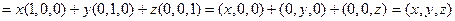 , т.е. любой вектор
, т.е. любой вектор 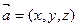 можно записать в виде
можно записать в виде 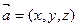 =
=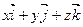 . Заметим также, что для скалярных произведений векторов
. Заметим также, что для скалярных произведений векторов 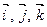 справедливы равенства
справедливы равенства 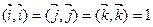 ,
, 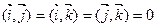 .
.
Пусть теперь 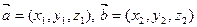 . Тогда по свойствам (3.2) – (3.6) скалярного произведения имеем
. Тогда по свойствам (3.2) – (3.6) скалярного произведения имеем 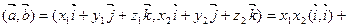
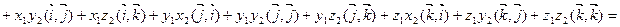
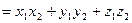 . Таким образом,
. Таким образом,
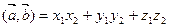 . (3.7)
. (3.7)
В частном случае при 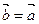 получаем
получаем 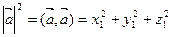 , поэтому длина вектора
, поэтому длина вектора  равна
равна
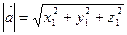 . (3.8)
. (3.8)
С помощью формулы (3.8) можно получить формулу для вычисления расстояния между точками 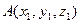 и
и 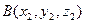 . Расстояние АВ равно длине вектора
. Расстояние АВ равно длине вектора 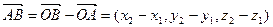 , где
, где 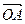 и
и 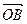 - радиус-векторы точек А и В соответственно. Поэтому по формуле (3.8) имеем
- радиус-векторы точек А и В соответственно. Поэтому по формуле (3.8) имеем
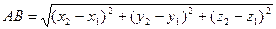 . (3.9)
. (3.9)
Пример 1. Найдем скалярное произведение векторов 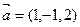 и
и 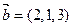 и угол между ними.
и угол между ними.
Решение. По формуле (3.7) 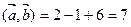 , по формуле (3.8)
, по формуле (3.8) 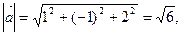
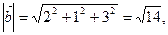 из формулы (3.1) находим
из формулы (3.1) находим
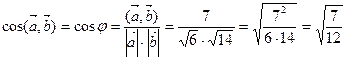 ,
, 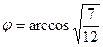 .
.
Пример 2. Найдем расстояние между точками А (2,3,6) и В (1,0,–2).
Решение. По формуле (3.9) находим 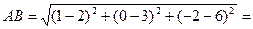
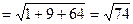 .
.
Рассмотрим теперь векторное произведение векторов.
Определение 2. Векторным произведением двух векторов 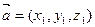 и
и 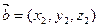 называется вектор
называется вектор
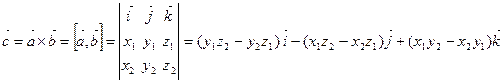 . (3.10)
. (3.10)
Другое определение, равносильное данному определению.
Определение 3. Векторным произведением двух векторов  и
и  называется вектор
называется вектор 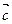 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) если векторы  и
и  коллинеарны, то
коллинеарны, то 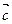 = 0;
= 0;
2) если векторы  и
и  не коллинеарны, то вектор
не коллинеарны, то вектор 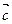 перпендикулярен векторам
перпендикулярен векторам  и
и  и направлен так, что система
и направлен так, что система 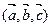 ориентирована так же, как и данная система координат. Длина же вектора
ориентирована так же, как и данная система координат. Длина же вектора 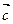 равна
равна
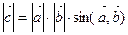 , (3.11)
, (3.11)
т.е. длина вектора 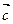 равна площади параллелограмма, построенного на векторах
равна площади параллелограмма, построенного на векторах  и
и  .
.
Замечание. Системы координат в пространстве могут быть ориентированы по- разному. Различают правую и левую системы координат. Правая система координат: если с конца вектора 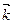 смотреть на вектор
смотреть на вектор 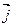 (т.е. на положительное направление оси Оу), то вектор
(т.е. на положительное направление оси Оу), то вектор 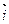 (т.е. ось Ох) находится справа. Левая система координат: если с конца вектора
(т.е. ось Ох) находится справа. Левая система координат: если с конца вектора 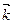 смотреть на вектор
смотреть на вектор 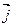 (т.е. на положительное направление оси Оу), то вектор
(т.е. на положительное направление оси Оу), то вектор 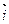 (т.е. ось Ох) находится слева. В определении 3 поставлено условие, что система
(т.е. ось Ох) находится слева. В определении 3 поставлено условие, что система 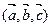 ориентирована так же, как система
ориентирована так же, как система 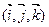 .
.
|
|
|
|
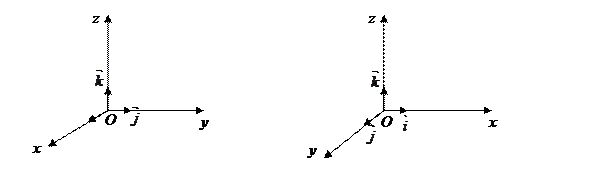
Правая система координат. Левая система координат.
Рассмотрим свойства векторного произведения.
1) 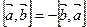 ; 2)
; 2) 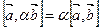 ; 3)
; 3) 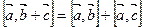 , где
, где 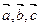 - произвольные векторы, α – число.
- произвольные векторы, α – число.
Все эти свойства получаются из формулы (3.10) и свойств определителя. Действительно,
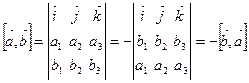 ;
; 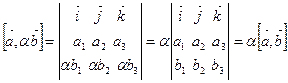 ;
; 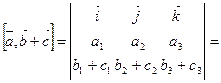
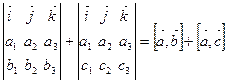 .
.
Пример 3. Верно ли, что 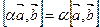 ?
? 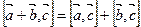 ?
?
Решение. Верно, так как по свойствам векторного произведения имеем 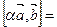
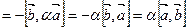 ,
, 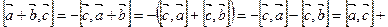
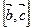 .
.
Пример 4. Найдем векторное произведение векторов 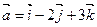 и
и 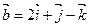 .
.
Решение. Запишем векторы  и
и  в координатной форме:
в координатной форме:  = (1,–2, 3),
= (1,–2, 3),  = (2, 1,–1). По формуле (3.10) имеем
= (2, 1,–1). По формуле (3.10) имеем
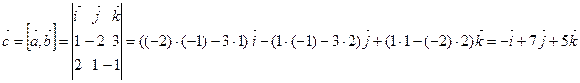 , т.е. вектор
, т.е. вектор 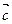 имеет координаты (–1, 7, 5).
имеет координаты (–1, 7, 5).
Пример 5. На плоскости даны три точки А (1;2), В (–1;3), С (0;–2). Найдем площадь параллелограмма, сторонами которого являются отрезки АВ и АС.
Решение. По определению 3 площадь параллелограмма, построенного на векторах  и
и  , равна длине вектора
, равна длине вектора 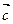 , являющегося векторным произведением векторов
, являющегося векторным произведением векторов  и
и  . Поэтому нам нужно найти длину вектора, являющегося векторным произведением векторов
. Поэтому нам нужно найти длину вектора, являющегося векторным произведением векторов 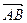 и
и 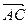 . Чтобы найти векторное произведение векторов
. Чтобы найти векторное произведение векторов 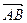 и
и 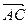 воспользуемся формулой (3.10). Найдем координаты этих векторов:
воспользуемся формулой (3.10). Найдем координаты этих векторов: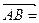
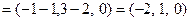 ,
, 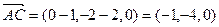 (третья координата равна нулю, так как векторы находятся в плоскости
(третья координата равна нулю, так как векторы находятся в плоскости 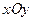 ). Тогда
). Тогда
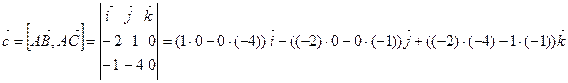 =
= 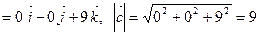 , т.е. искомая площадь параллелограмма равна 9.
, т.е. искомая площадь параллелограмма равна 9.
Заметим, что из определения 3 следует, что векторы  и
и  коллинеарны тогда и только тогда, когда их векторное произведение равно нулю. Согласно первому условию определения 3 из коллинеарности векторов следует равенство нулю их векторного произведения, а из формулы (3.11) получаем обратное утверждение, так как для ненулевых векторов из равенства нулю векторного произведения следует равенство нулю синуса угла между векторами, т.е. этот угол равен либо 0, либо
коллинеарны тогда и только тогда, когда их векторное произведение равно нулю. Согласно первому условию определения 3 из коллинеарности векторов следует равенство нулю их векторного произведения, а из формулы (3.11) получаем обратное утверждение, так как для ненулевых векторов из равенства нулю векторного произведения следует равенство нулю синуса угла между векторами, т.е. этот угол равен либо 0, либо 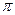 , что и означает коллинеарность векторов.
, что и означает коллинеарность векторов.
Равенство нулю векторного произведения означает, что координаты вектора 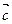 равны нулю. Из равенства (3.10) получаем, что одновременно
равны нулю. Из равенства (3.10) получаем, что одновременно 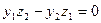 ,
, 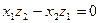 и
и 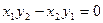 .Отсюда
.Отсюда 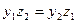 ,
, 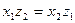 и
и 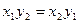 ,
, 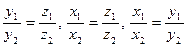 , т.е.
, т.е. 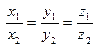 . Таким образом, получаем, что векторы коллинеарны тогда и только тогда, когда их координаты пропорциональны.
. Таким образом, получаем, что векторы коллинеарны тогда и только тогда, когда их координаты пропорциональны.
Например, векторы 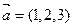 и
и 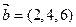 коллинеарны, так как
коллинеарны, так как 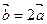 .
.
Рассмотрим, наконец, смешанное произведение векторов.
Определение 4. Смешанным (векторно-скалярным) произведением трех векторов  ,
,  и
и 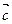 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 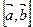 на вектор
на вектор 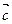 . Обозначается
. Обозначается 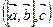 .
.
Получим формулу для вычисления смешанного произведения векторов 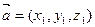 ,
, 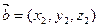 и
и 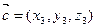 .По формулам (3.10) и (3.7), определению определителя 2-го порядка и формуле разложения определителя 3-го порядка по элементам третьей строки имеем
.По формулам (3.10) и (3.7), определению определителя 2-го порядка и формуле разложения определителя 3-го порядка по элементам третьей строки имеем
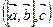 =
=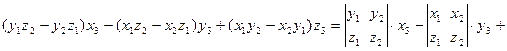
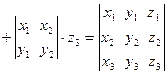 . Таким образом, смешанное произведение трех векторов вычисляется по формуле
. Таким образом, смешанное произведение трех векторов вычисляется по формуле
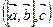 =
= 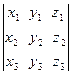 . (3.12)
. (3.12)
|
|
|











|
|
|
|
|





 В силу определения скалярного произведения
В силу определения скалярного произведения 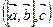 =
=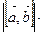 пр
пр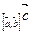 . Поскольку │пр
. Поскольку │пр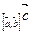 │- высота параллелепипеда, построенного на векторах
│- высота параллелепипеда, построенного на векторах  ,
,  и
и 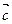 , в основании которого лежит параллелограмм, имеющий площадь
, в основании которого лежит параллелограмм, имеющий площадь 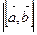 , то │
, то │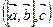 │- объем этого параллелепипеда. Таким образом, модуль смешанного произведения векторов
│- объем этого параллелепипеда. Таким образом, модуль смешанного произведения векторов  ,
,  и
и 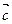 равен объему параллелепипеда, построенного на этих векторах.
равен объему параллелепипеда, построенного на этих векторах.
Если векторы  ,
,  ,
, 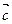 лежат в одной плоскости, то векторы
лежат в одной плоскости, то векторы 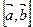 и
и 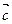 перпендикулярны, поэтому
перпендикулярны, поэтому 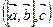 = 0. Обратно, если
= 0. Обратно, если 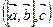 = 0, то
= 0, то 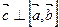 , поэтому
, поэтому  ,
,  и
и 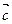 лежат в одной или параллельных плоскостях. Таким образом, условие
лежат в одной или параллельных плоскостях. Таким образом, условие 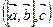 = 0 является необходимым и достаточным условием компланарности трех векторов
= 0 является необходимым и достаточным условием компланарности трех векторов  ,
,  и
и 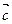 .
.
Свойства смешанного произведения:
1. Смешанное произведение не изменяется при циклической перестановке перемножаемых векторов: 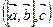 =
= 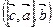 =
= 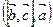 .
.
Это следует из свойства б) определителя:
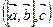 =
= 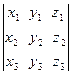 =
= 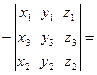
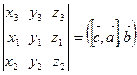 ,
,
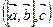 =
= 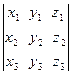 =
= 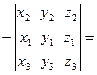
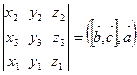 .
.
2. Смешанное произведение меняет знак при перестановке двух векторов, например,
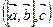 =
= 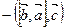 . Это следует из того же свойства б) определителя.
. Это следует из того же свойства б) определителя.
Пример 6. Проверим, компланарны ли векторы 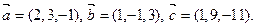
Решение. Вычислим смешанное произведение векторов  ,
,  и
и 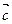 :
: 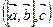 = =
= =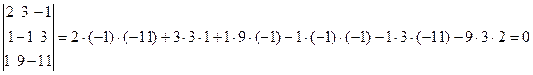 , т.е. данные векторы компланарны.
, т.е. данные векторы компланарны.
Пример 7. Выясним, лежат ли точки А (0;0;1), В (2;3;5), С (6;2;3), D (3;7;2) в одной плоскости. Если нет, то найдем объем параллелепипеда с вершинами в этих точка.
Решение. Данные точки лежат в одной плоскости, если в одной плоскости лежат векторы 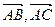 и
и 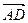 . Найдем их координаты и вычислим смешанное произведение:
. Найдем их координаты и вычислим смешанное произведение: 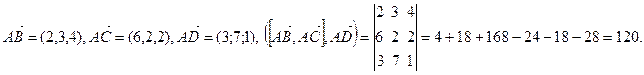 Смешанное произведение не равно нулю, поэтому векторы не компланарны и не лежат в одной плоскости. Объем параллелепипеда равен модулю смешанного произведения, т.е. равен 120 ед
Смешанное произведение не равно нулю, поэтому векторы не компланарны и не лежат в одной плоскости. Объем параллелепипеда равен модулю смешанного произведения, т.е. равен 120 ед .
.
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 1623; Нарушение авторских прав?; Мы поможем в написании вашей работы!