
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системы линейных однородных уравнений
,,.
Откуда 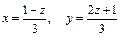 .
.
Ответ: 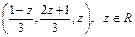 .
.
Рассмотрим систему линейных однородных уравнений:
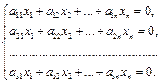 (7.9)
(7.9)
Очевидно, что 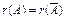 , т.к.
, т.к. 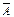 отличается от А наличием нулевого столбца. Значит, система линейных однородных уравнений (СЛОУ) всегда
отличается от А наличием нулевого столбца. Значит, система линейных однородных уравнений (СЛОУ) всегда
совместна. Пусть 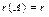 .
.
Если 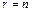 , то СЛОУ имеет единственное решение. Если
, то СЛОУ имеет единственное решение. Если 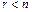 - то множество решений.
- то множество решений.
Теорема 7.10 выражает свойства решений СЛОУ.
| Th.7.10 | Если 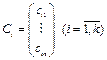 – решение СЛОУ (7.9), то любая их линейная комбинация является решением СЛОУ (7.9). – решение СЛОУ (7.9), то любая их линейная комбинация является решением СЛОУ (7.9).
|
Доказательство.
СЛОУ (7.9) запишем в матричном виде: АХ = 0. Т.к. 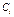 - решение СЛОУ (7.9), то
- решение СЛОУ (7.9), то 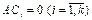 .
.
Рассмотрим 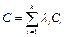 . Тогда
. Тогда 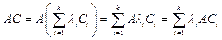 .
.
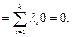 Значит, С – решение СЛОУ (7.9)
Значит, С – решение СЛОУ (7.9)  .
.
Следствие 1. Множество решений СЛОУ образует линейное подпространство пространства 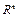 . .
|
Def.Фундаментальной системой решений (ФСР) СЛОУ называется базис линейного подпространства ее решений.
Заметим, что СЛОУ имеет ФСР только в том случае, если она неопределенная. Причем таких ФСР бесконечное множество.
| Th.7.11 | (о ФСР СОЛУ)
Пусть в СЛОУ (7.9) 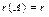 . Если . Если 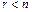 , то ФСР СЛОУ состоит из n-r решений. , то ФСР СЛОУ состоит из n-r решений.
|
Доказательство.
Пусть 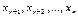 - свободные переменные СЛОУ (7.9). Рассмотрим произвольный определитель (n-r)-го порядка
- свободные переменные СЛОУ (7.9). Рассмотрим произвольный определитель (n-r)-го порядка 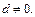
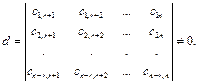 (7.10)
(7.10)
Выберем элементы определителя d в качестве свободных переменных, получим n-r решений СЛОУ (7.9):
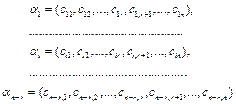 (7.11)
(7.11)
Покажем, что 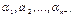 – базис линейного подпространства решений СЛОУ. Для этого необходимо показать, что они линейно независимы и любое другое решение СЛОУ является их линейной комбинацией.
– базис линейного подпространства решений СЛОУ. Для этого необходимо показать, что они линейно независимы и любое другое решение СЛОУ является их линейной комбинацией.
n -мерные векторы 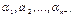 – линейно независимы. Действительно, если бы они были линейно зависимы, то эта зависимость перенеслась бы и на последние n-r элементов, т.е на строки определителя (7.10). Но тогда, согласно критерию равенства нулю определителя,
– линейно независимы. Действительно, если бы они были линейно зависимы, то эта зависимость перенеслась бы и на последние n-r элементов, т.е на строки определителя (7.10). Но тогда, согласно критерию равенства нулю определителя, 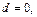 а это не так.
а это не так.
Пусть 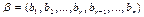 – произвольное решение СЛОУ (7.9). Покажем, что
– произвольное решение СЛОУ (7.9). Покажем, что 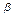 – линейная комбинация
– линейная комбинация 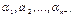 .
.
Рассмотрим (n-r)-мерные векторы, компонентами которых служат строки определителя d:
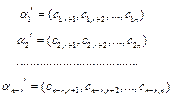 (7.12)
(7.12)
Векторы 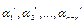 – линейно независимы, т.к.
– линейно независимы, т.к. 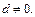 Введем в рассмотрение еще один (n-r)-мерный вектор
Введем в рассмотрение еще один (n-r)-мерный вектор 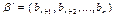 (его компоненты совпадают с последними n-r компонентами вектора
(его компоненты совпадают с последними n-r компонентами вектора 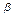 ).
).
Система (n-r)-мерных векторов 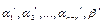 – линейно зависима согласно теореме 7.7. Значит, на основании теоремы 7.6 можно сделать вывод о том, что
– линейно зависима согласно теореме 7.7. Значит, на основании теоремы 7.6 можно сделать вывод о том, что
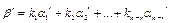 (7.13)
(7.13)
Рассмотрим n-мерный вектор 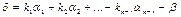 . На основании теоремы 7.10 можно утверждать, что
. На основании теоремы 7.10 можно утверждать, что 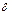 – решение СЛОУ (7.9). Из соотношения (7.13) следует, что все компоненты вектора
– решение СЛОУ (7.9). Из соотношения (7.13) следует, что все компоненты вектора 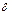 , соответствующие свободным переменным равны 0. Но тогда
, соответствующие свободным переменным равны 0. Но тогда 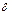 – тривиальное решение СЛОУ (7.9), т.е.
– тривиальное решение СЛОУ (7.9), т.е. 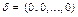 . Значит,
. Значит, 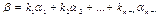 .
.
Таким образом, доказано, что 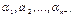 образуют ФСР СЛОУ (7.9)
образуют ФСР СЛОУ (7.9)  .
.
Теорема 7.11 дает практический способ нахождения ФСР для СЛОУ: свободным переменным придают значения элементов (по строкам) любого определителя (n-r)-го порядка, отличного от нуля. Полученные при этом решения СЛОУ образуют ФСР. В качестве указанного определителя удобно брать определитель единичной матрицы (n-r)-го порядка.
N. Найти ФСР для СЛОУ 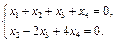
Решение. 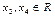 – свободные переменные.
– свободные переменные.
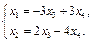
Придавая свободным переменным значения элементов по строкам определителя 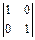 , вычисляем соответствующие значения связных переменных.
, вычисляем соответствующие значения связных переменных.
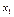
| 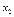
| 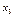
| 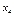
|
| -3 | |||
| -4 |
Ответ: 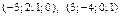 – ФСР.
– ФСР.
Рассмотрим связь, которая существует между решениями однородных и неоднородных систем. Путь дана система линейных неоднородных уравнений (СЛНУ):
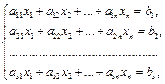 (7.14)
(7.14)
Def. СЛОУ, полученная из системы (7.14) заменой свободных членов нулями, называется приведенной системой для СЛНУ.
Так СЛОУ (7.9) является приведенной для СЛНУ (7.14).
Следующие две теоремы отражают связь между решениями этих систем.
| Th.7.12 | Сумма любого решения СЛНУ (7.14) и приведенной системы (7.9) снова будет решением СЛНУ (7.14) |
Доказательство.
Запишем обе системы в матричном виде:
(7.14)  АХ=В
АХ=В
(7.9)  АХ=0
АХ=0
Пусть С – решение СЛНУ (7.14), а Р – решение СЛОУ (7.9). Тогда АС=В и АР=0.
А(С+Р)=АС+АС=В+0=В. Т.е. Р+С – решение СЛНУ (7.14)  .
.
| Th.7.13 | Разность двух решений СЛНУ (7.14) есть решение СЛОУ (7.9) |
Доказательство.
Запишем обе системы в матричном виде:
(7.14)  АХ=В
АХ=В
(7.9)  АХ=0
АХ=0
Пусть 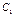 и
и 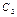 - решения СЛНУ (7.14). Тогда
- решения СЛНУ (7.14). Тогда 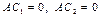
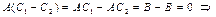
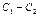 – решение СЛОУ (7.9)
– решение СЛОУ (7.9)  .
.

|
Дата добавления: 2013-12-12; Просмотров: 1791; Нарушение авторских прав?; Мы поможем в написании вашей работы!