Лінійні диференціальні рівняння вищих порядків зі сталими коефіцієнтами

Розглянемо лінійне однорідне рівняння другого порядку зі сталими коефіцієнтами

, (13.41)

де - дійсні числа. Знайдемо два лінійно незалежних розв’язки рівняння (13.41).

Шукаємо їх у вигляді , де - дійсне число, тоді

В силу того, що , то для знаходження маємо характеристичне рівняння:

. (13.42)

Можливі наступні випадки:

1) - дійсні, , тоді фундаментальною системою розв’язків (13.41) будуть . Загальний розв’язок (13.41) матиме вигляд:

;

2) - комплексно-спряжені, тобто: . Легко перевірити, що фундаментальною системою розв’язків (13.41) будуть . Загальний розв’язок (13.41) матиме вигляд:

;

3) - дійсні, , тоді , а шукаємо у вигляді , де - невідома функція. Тоді

.

Підставивши 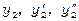в (41), одержимо:

. (13.43)

В силу того, що - кратний корінь характеристичного рівняння, то і (13.43) набуде вигляду: , звідки . Оберемо , тоді та . Загальний розв’язок (41) матиме вигляд:

.

Розглянемо лінійне однорідне диференціальне рівняння порядку 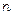зі сталими коефіцієнтами

. (13.44)

Аналогічно складаємо характеристичне рівняння:

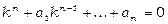. (13.45)

Тоді загальний розв’язок (44) будується в залежності від характеру коренів рівняння (45):

1) кожному дійсному простому кореню відповідає частинний розв’язок ;

2) кожній парі комплексно-спряжених простих коренів 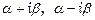відповідають два частинних розв’язки: ;

3) кожному дійсному кореню кратності відповідають лінійно незалежних частинних розв’язків: ;

4) кожній парі комплексних спряжених коренів 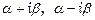кратності відповідають частинних розв’язків:

Загальна кількість частинних розв’язків повинна дорівнювати порядку диференціального рівняння.

У випадку лінійного неоднорідного диференціального рівняння порядку 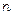зі сталими коефіцієнтами та спеціальною правою частиною для знаходження частинного розв’язку застосовують метод невизначених коефіцієнтів.

Нехай - многочлен 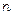-ї степені, тоді:

· якщо 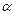не є коренем характеристичного рівняння, то частинний розв’язок шукають у вигляді - многочлен 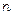-ї степені з невизначеними коефіцієнтами;

· якщо 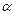є коренем кратності характеристичного рівняння, то частинний розв’язок шукають у вигляді - многочлен 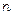-ї степені з невизначеними коефіцієнтами.

Нехай - многочлени відповідно 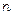-ї та -ї степені, тоді:

· якщо число не є коренем характеристичного рівняння, то частинний розв’язок шукають у вигляді де - многочлени -ї степені з невизначеними коефіцієнтами, ;

· якщо число є коренем кратності характеристичного рівняння, то частинний розв’язок шукають у вигляді 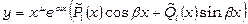, де - многочлени -ї степені з невизначеними коефіцієнтами, .

Зауважимо, що тоді, коли містить лише або 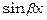частинний розв’язок шукають у вигляді, що включає обидві функції.

Невизначені коефіцієнти можна знайти із системи лінійних рівнянь, які одержуються в результаті прирівнювання коефіцієнтів подібних членів у правій та лівій частинах початкового рівняння після підстановки в нього частинного розв’язку та його похідних.

Приклад 21. Розв’язати диференціальне рівняння .

Характеристичне рівняння має корені . Загальний розв’язок відповідного однорідного рівняння .

У заданому рівнянні , звідки , яке не є коренем характеристичного рівняння. Тому шукаємо частинний розв’язок неоднорідного рівняння у вигляді: .

Обчислимо похідні 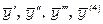та підставимо в задане рівняння:

.

Прирівнюємо коефіцієнти при однакових степенях змінної, тоді та . Остаточно, загальний розв’язок рівняння має вигляд: .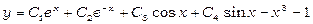

Приклад 22. Розв’язати задачу Коші

.

Характеристичне рівняння має корені . Загальний розв’язок відповідного однорідного рівняння . Частинний розв’язок неоднорідного рівняння шукаємо у вигляді: , тоді

.

Прирівнюємо коефіцієнти при однакових тригонометричних функціях

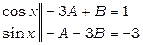, звідки .

Отже, загальний розв’язок рівняння має вигляд: .

Для розв’язання задачі Коші знаходимо: , тоді

; .

Приклад 23. Розв’язати диференціальне рівняння

.

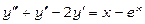Характеристичне рівняння має корені . Загальний розв’язок відповідного однорідного рівняння .

У даному рівнянні , тому, користуючись принципом накладання та враховуючи, що є простими коренями характеристичного рівняння., шукаємо частинний розв’язок неоднорідного рівняння у вигляді: . Отже,

,

звідки

.

Остаточно маємо: .

Дата добавления: 2014-01-04