Законы распределения случайных ПИ и РИ

1. Равномерные распределения – РИ Х_і и ПИ распределены внутри заданого интервала с одинаковой плотностью вероятности, как показано на рис. 2.12.

Рис.2.12а. Равномерное Рис.2.12б. Равномерное

нелинейное распределение РИсиметричное распределение РИ

(2.33) (2.34)

Равномерно распределены погрешности от: изменения напряжения питания; квантования при оцифровке измерительных аналоговых сигналов; сухого трения; не исключенные остатки систематических погрешностей после их алгоритмической или приборной компенсации (после вычисления поправки q, q= - Δ_с).

2. Триугольное распределение (Закон Симпсона). Вид треугольного распределения случайных РИ и ПИ указан на рис. 2.13.

Рис.2.13а. Треугольное Рис.2.13б. Симетричное

несиметричное распределение ПИраспределение ПИ

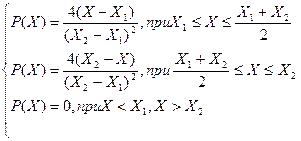
(2.35) (2.36)

Таким образом распределены погрешности от суммы (разности) двух равномернораспределенных СВ; суммарная погрешность от квантования двух смешаных случайных сигналов.

3. Нормальное распределение (Закон Гауса).

Это наиболее распространенный закон распределения случайных ПИ и РИ, что обьясняется Центральной Предельной Теоремой Вероятности (ЦПТ). ЦПТ утверждает, что распределение СВ (РИ и ПИ) будет близко к нормальному, если РИ формируется под влиянием большого числа независимодействующих факторов, каждый из которых оказывает незначительное действие на РИ по сравнению с суммарным действием всех факторов.

В соответствии с теоремой случайная погрешность подчиняется нормальному закону, если она является суперпозицией (суммы) четырех и более независимых случайных равновеликих погрешностей.

, n4. – Сумарная случайная погрешность распределения по нормальному закону.

В реальных условиях условие (2.37) выполняется постоянно, поэтому в реальных условиях эксплуатации считают, что распределены нормально.

4. Графическая интерпретация нормального закона распределения СВ показана на рис. 2.14.

Рис.2.14.

Показаные на рис. 2.14. графики нормального закона описываются формулами (2.38):

δ_х= - СКО СВ х, которое определяется по ранее приведеным формулам.

На рис. 2.14. показаны два графика, для которых выполняется соотношение: δ_х1<δ_х2. (2.39)

Это означает, что в первом случае измерительная задача решена с большой точностью (большее количество результатов наблюдения распределено вблизи М_х, а следовательно и меньшая погрешность РИ). Таким образом необходимо стремится к дифференциальным функциям распределения с меньшим СКО, желательно иметь больший колокол. Дополнительные свойства функции:

1)Р(Х) имеет max, при Х= М_х;

2)с ростом случайной погрешности, , независимо от знака в левой части или правой, т.е. вероятность появления больших случайных погрешностей очень мала. Если такая погрешность появилась, то функция говорит, что её быть не должно, это практически однозначно можно трактовать как грубую погрешность, ошибку оператора, однозначно должна быть исключена.

СВназывается центрированной, если .

Рассмотрим нормальное распределение центрированной случайной погрешности.

При этом будем полагать, что математическое ожидание этой погрешности равно 0, т.е. система отсутствует, а имеется только случайная составляющая.

На практикетакая ситуация соответствует случаю, когда выполнена алгоритмическая или приборная компенсация систематической составляющей погрешности.

График показан на рис. 2.15.

Рис.2.15.

ДФР (дифференциальная функция распределения)

, (2.40)

– СК , .

Вид формулы (2.40) в размерности ИВ неудобен и под каждую ИВ необходимо записывать свою формулу. В практической метрологии для исключения этого неудобства принята нормируема форма нормального распределения центрированной случайной погрешности, которая получается после подстановки в (2.40).

, (2.41)

(согласно рисунку 2.16), где - коэффициент, принадлежащий интервалу

- СКО результат единичного наблюдения, рассчитан по ранее приведенной формуле.

Рис.2.16.

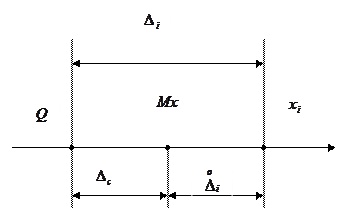
В результате этой подстановки получается простое универсальное, выражается для ДФР в нормированном безразмерном виде:

. (2.42)

И всё зависит от выбранного . Эта величина коэффициента исходит из важности решаемой измерительной задачи. Рекомендации по выбору коэффициента будут рассмотрены далее.

График функции показан на рис. 2.17. Данная функция табулирования (данная в виде таблицы).

Рис.2.17.

В измерительной технике нормально распределены следующие случайные погрешности:

1) от среднечастотных и высокочастотных шумов и флюктуаций, как правило, источником которых в активных электронных компонентах;

2) из-за случайной нестабильности электромеханических узлов приборов;

3) суммарная случайная погрешность при большом () числе независимых равновеликих составляющих. Такой закон практически охватывает до 90% всех решаемых на практике задач.

2.7 Определение доверительных интервалов для истинного значения ИВ, имеющей нормальное распределение с известным СКО ()

2.7.1 Определение ДИ по результату однократного измерения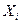

ДИ – доверительный интервал.

Полагаем, что 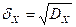- известно для данной измерительной задачи до проведения конкретного измерения, как правило, это СКО определяется на основе статических данных о выбранном средстве измерения и методе измерения.

Для данной ИВ на рис. 2.18 показан график нормального распределения с в точке (это означает, что все систематические погрешности исключены)

Рис 2.18.

Введем доверительный интервал:

где - коэффициент, зависящий от выбранной доверительной вероятности. Определим вероятность того, что результат единичного измерения 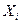окажется в доверительном интервале.

Согласно ранее введенных определений о вероятности – данная вероятность равна площади фигуры. Вычислим эту вероятность:

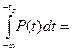
-, (2.44)

,

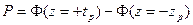. (2.45)

Из значения интегральной функции распределения, вычисленной в точках и 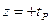по соответствующим таблицам.

Вид этой функции распределения показан на (рис. 2.19), значение этой функции для наиболее применяемых параметров таблицы 2.1.

В общем, интегральная функция распределения определяется по формуле:

(2.46) и табулирована для всех параметров 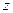, используемых в измерительной технике, .

График функции показан на рис.2.19, а её значения показаны в таблице 2.1.

z	-3.5	-3	-2	-1					3.5
	0.00023	0.00135	0.0228	0.1587	0.5	0.8413	0.9778	0.99863	0.99977

Рис.2.18.

Согласно рис. 2.18 предельные значения РИ называется доверительными границами РИ, а вероятность (см. ф. 2.45) – доверительной вероятностью того, что результат единичного наблюдения 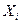попадает в заданный доверительный интервал, т.е. 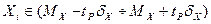(2.47)

С вероятностью РИ 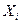может оказаться за границами доверительного интервала. Определим значения вероятностей для наиболее распространенных в измерительной технике значений . При этом отметим, что при решении измерительных задач выбирают:

- для лабораторных условий и измерительных задач не связанных с жизнью людей;

- в бортовых условиях подвижных объектов гражданского назначения, если решение измерительных задач не связано с жизнью людей (ВВ. );

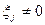- для бортовых измерений, объектов специального (военного назначения) и при решении измерительных задач не связано с жизнью людей (ВВ. ).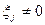

За оценку истинного значения ИВ принимают математическое ожидание, т.е. . Результат вычисления данных вероятностей и их графические интерпретации показаны на рис. 2.20

Рис.2.20.

Рис. 2.20 показывает, что с вероятностью 68% результат единичного измерения 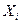принадлежит интервалу , а с вероятностью 32% будет лежать вне этого интервала.

Таким образом вероятность нахождения результата единичного измерения 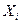в доверительном интервале определяемым выбранным значениям , определяется выражением:

(2.48) показывает, что оценка истинного значения ИВ с доверительной вероятностью находится внутри доверительного интервала.

, где 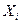- результат единичного измерения.

РИ, определяемый на основе единичного измерения записывается в виде:

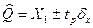, Р (2.49)

.

РИ группового измерения записывается в виде

(2.50)

– математическое ожидание, среднее арифметическое результатов единичных измерений.

.

Пример:

В результате измерения длинны, получим линейный размер =50,048 мм СКО такого измерительного процесса, указанного в паспорте измерения (при условии, что измерение не является грубым).

=0,4 мкм = 0,0004 мм;

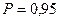
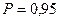. (2.51)

2.7.2 Определение точечных оценок математического ожидания , СКО и по экспериментальным данным (практические формулы)

До этого мы полагали, что известны законы и параметры распределения случайных РИ и ПИ. Задача – определить основные параметры распределения случайных РИ и их погрешностей по экспериментальным данным, т.е. на основании выборки объема () ограниченного ряда числовых значений результатов единичных наблюдений .

Оценк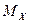и и , будем обозначать . Эти оценки должны быть:

- точечными, т. е. выражается одним числом;

- несмещенными, т. е. МО , т. е. ;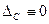

- состоятельный, т. е. при увеличении её отличие от оцениваемого параметра может быть сделано сколь угодно малым;

- эффективны, т.е. её дисперсия (СКО) должна быть меньше дисперсии СКО любой другой оценки, которую можно предложить.

Практические формулы, по которым определяются выше названы оценки:

1. МО

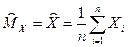(2.52)

2. СКО единичного измерения

, (2.53)

При 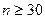может быть использована приближенная формула для оценки СКО:

. (2.54)

3. СКО среднего арифметического или СКО группового измерения

, (2.55)

(2.56)

Запишем два примера и сравним их между собой.

Пример 1:

В результате оценки по экспериментальным данным получим 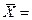25,01 мм; 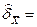0,0005 мм; .

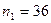Пример 2:

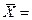25,01 мм; 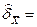0,0005 мм; .

Если выполняется, сравним эти результаты между собой.

Если выполняется всего одно измерение:

мм;

мм.

(2.57)

(2.57) показывает, что во 2 – ом случае измерения выполнялись в два раза точнее СИ одного и того же результата групповых измерений; удалось достичь, уменьшив в 4 раза число наблюдений и увеличив в 4 раза быстродействие результата, что особенно важно, если ИВ является динамической.

Дата добавления: 2014-01-07