Примеры. 1) Функция суммы, определяемая равенством , является примитивно рекурсивной, так как она задаётся схемой примитивной рекурсии

1) Функция суммы, определяемая равенством 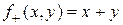, является примитивно рекурсивной, так как она задаётся схемой примитивной рекурсии

,

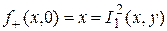
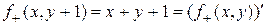т.е. 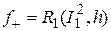, где 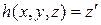, причём функции g и h являются примитивно рекурсивными.

2) Функция арифметического вычитания 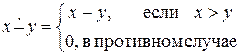. (Доказать самостоятельно её примитивную рекурсивность).

Арифметизированные логические функции также являются примитивно рекурсивными, так, например, 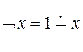. Также с помощью арифметического вычитания можно выразить Ù и Ú (самостоятельно). Из функциональной полноты множества функций 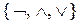следует примитивная рекурсивность всех логических функций.

Определение. Отношение 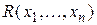называется примитивно рекурсивным, если его характеристическая функция

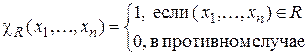
примитивно рекурсивна.

Так как существует взаимно однозначное соответствие между отношениями и предикатами, то 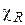будет характеристической функцией и для соответствующего отношению R предиката.

Например, предикат 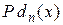делимости нацело числа x на n является примитивно рекурсивным, так как его характеристическая функция 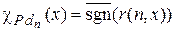, где 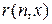– функция, вычисляющая остаток от целочисленного деления x на n, примитивно рекурсивна.

Определение. Оператор называется примитивно рекурсивным, если он сохраняет примитивную рекурсию функций.

Например, условный оператор 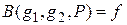, где

,

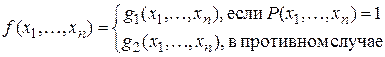является примитивно рекурсивным. Примитивно рекурсивными являются также операторы конечного суммирования и конечного произведения

,

.

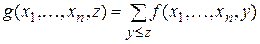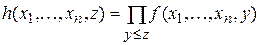Определение. Ограниченный оператор наименьшего числа, называемый также ограниченным оператором минимизации (ограниченный m-оператор), определяется равенством

.

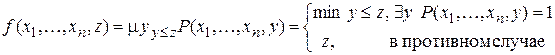Для заданного числа z он определяет минимальное значение у £ z, для которого Р (у) = 1.

Пример. Пусть задан предикат 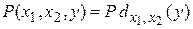, который принимает значение 1, если число y нацело делится на 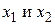. Применение ограниченного оператора минимизации к предикату 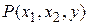имеет результатом функцию .

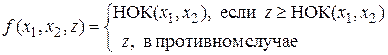Ограниченный оператор минимизации примитивно рекурсивен.

Он является средством построения обратных функций. Функция 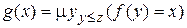является обратной к функции 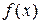. Например, функция целочисленного деления z на x определяется ограниченным оператором минимизации

.

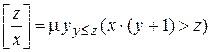(Здесь надо найти наименьшее у, чтобы x× (y + 1) > z).

В результате рассмотрения примеров функций, которые все являлись примитивно рекурсивными, возникает вопрос: существуют ли не примитивно рекурсивные функции. В данном случае ответ положительный, класс примитивно рекурсивных функций не исчерпывает класс всех вычислимых функций.

Функция Аккермана. Построим функцию, которая является вычислимой, но не примитивно рекурсивной.

Определим последовательность функций 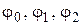по правилу 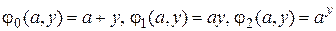. Функции 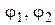обладают следующими свойствами

1) , ;

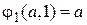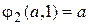2) , .

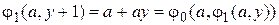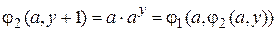Продолжим последовательность по рекуррентному правилу 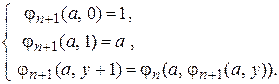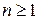2):

() (2)

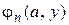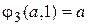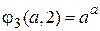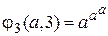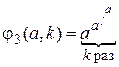Функции примитивно рекурсивны и растут очень быстро. Так, например, , , , ¼, , ¼

Зафиксируем 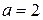и рассмотрим последовательность функций 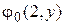, , 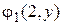¼, 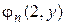, ¼ Определим функцию 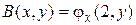, которая обладает свойствами

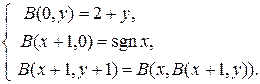(3)

Функция Аккермана 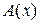определяется как диагональ функции 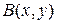, т.е. =.

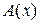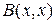Функция Аккермана является вычислимой, так как соотношения (2), (3) позволяют построить программу для её вычисления. Однако данная функция не является примитивно рекурсивной, так как она в силу (3) является двукратно рекурсивной (рекурсия идёт по обоим аргументам – не положено).

Поэтому средства построения вычислимых функций нуждаются в расширении. Если добавить к примитивно рекурсивным функциям оператор кратной рекурсии при определённом n, то для любого n можно построить функцию, которая является 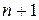-рекурсивной, но не n -рекурсивной. Следовательно, оператор кратной рекурсии не замыкает класс вычислимых функций. Средством завершающим построение вычислимых функций является m-оператор.

Определение. Неограниченный m-оператор для функции 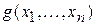, который обозначается 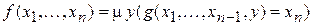, определяется как минимальное из значений y,являющихся решением уравнения .

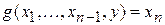Неограниченный m-оператор часто называют просто m-оператором. Также используют представление m-оператора в ви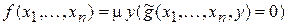де , где 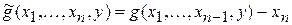. Алгоритм вычисления 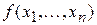состоит в вычислении значений 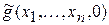, , 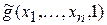¼ до тех пор пока не получим 0-го значения. Также как и ограниченный оператор минимизации, m-оператор используют для построения обратных функций.

Определение. Функция называется частично рекурсивной, если она может быть построена из 0, функци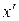й и 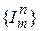с помощью конечного числа применений операторов суперпозиции, примитивной рекурсии и m-оператора.

Частично рекурсивная функция может быть определена не для всех значений. Например, функция обратная к функции следования 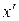, задаваемая равенством 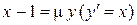, не определена при .

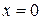Определение. Частично рекурсивная функция называется общерекурсивной, если она всюду определена.

Теорема 2.1. Классы вычислимых и частично рекурсивных функций совпадают.

3. Временная сложность алгоритма. Классы P и NP.

При решении массовой задачи P требуется не просто найти алгоритм, решающий эту задачу, но построить наиболее эффективный алгоритм.

Под эффективностью алгоритма понимают затраты всех вычислительных ресурсов, необходимых для работы алгоритма. Основное внимание сосредотачивается на затратах времени – временной сложности алгоритма. Кроме того, анализируется еще и сложность по памяти.

Время работы алгоритма удобно выражать в виде функции от переменной, характеризующей размер индивидуальной задачи (размерности задачи) т.е. объём данных, требуемых для описания этой задачи. Например, для графа, задаваемого списками инцидентности, размерность задачи представляется как пара (n, m). Эта функция каждой входной длине n ставит в соответствие максимальное время, затрачиваемое алгоритмом на решение индивидуальной задачи этой длины. Значение времени зависит от схемы кодирования и вычислительного устройства, определяющего время работы. Нас же будет в дальнейшем интересовать не точная временная сложность алгоритма, а асимптотическая сложность, которая определяется скоростью роста числа шагов алгоритма при неограниченном увеличении размерности задачи.

Для сравнения скорости роста двух функци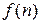й и 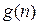будем использовать обозначения 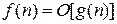или .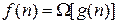

Определение. Будем говорить, что функция 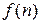имеет порядок роста не более чем функция 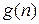, что обозначается 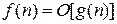, тогда и только тогда, когда существуют 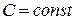и 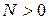, такие, что

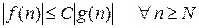
Будем говорить, что функция 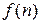имеет порядок роста не менее чем функция 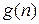, что обозначается 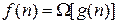, тогда и только тогда, когда существуют 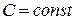и 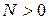, такие, что

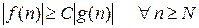
Например, для функции

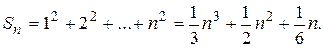
в силу принятых обозначений, можно записать, что 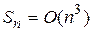или 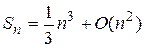. В общем случае, если 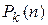– многочлен степени 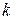, то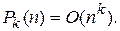

Непосредственно из определения вытекают следующие свойства:

;

;

.

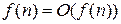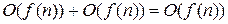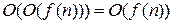Если рассматривается представление алгоритма, как ДМТ-программа M, то временная сложность алгоритма 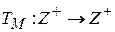определяется равенством

.

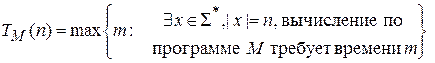ДМТ-программа M называется полиномиальной, если существует полином некоторой степени k, такой что 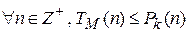, т.е. 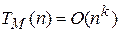. С помощью этого понятия введём класс языков P.

Класс языков P образуют языки, для которых существует полиномиальная ДМТ-программа распознавания, т.е.

.

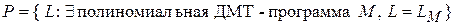Будем говорить, что задача распознавания P принадлежит классу задач P при схеме кодирования e, если язык 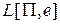принадлежит классу языков P.

Класс NP. Однако не для любой задачи полиномиальная программа существует. Рассмотрим, например, задачу коммивояжера. Как задача распознавания она формулируется следующим образом: дано множество городов, расстояния между ними и число B > 0. Существует ли проходящий через все города маршрут длины, не превосходящей B.

Полиномиальный алгоритм решения этой задачи неизвестен. Опишем вначале неформально класс задач, к которому она принадлежит, а потом формализуем это определение.

Неформально класс NP можно определить с помощью недетерминированного алгоритма. Он состоит из 2-х стадий: угадывания и проверки. По индивидуальной задаче I происходит угадывание S – ответа задачи. Для задачи о коммивояжере это будет вариант пути между вершинами графа. Затем I и S подаются на стадию проверки, которая выполняется детерминированным образом. В нашем примере проверяется, является ли предъявленный путь гамильтоновым циклом, вычисляется его длина и сравнивается с границей B.

Недетерминированный алгоритм решает задачу распознавания P, если 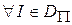выполняются свойства:

1) Если 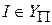, то $ вариант S, угадывание которого приводит к положительному ответу;

2) Если 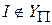, то такого варианта не существует (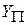– множество индивидуальных задач с ответом «да»).

Таким образом, класс задач NP – это класс всех задач распознавания, которые при разумном кодировании могут быть решены недетерминированным алгоритмом за полиномиальное время.

Формальным эквивалентом для недетерминированного алгоритма является программа для недетерминированной одноленточной машины Тьюринга (НДМТ). Структура НДМТ отличается от ДМТ наличием угадывающего модуля со своей читающе/пушущей головкой, связанного с управляющим устройством. Программа для НДМТ задаётся тем же набором 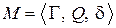, что и для ДМТ.

Порядок работы НДМТ под управлением программы .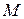

1. Входное слово 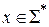записывается на ленте в ячейках с номерами 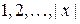(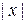– длина слова x), все другие ячейки содержат пустой символ. Читающая/пишущая головка управляющего устройства находится над ячейкой с номером 1, а угадывающего модуля – над ячейкой –1.

2. Управление передаётся угадывающему модулю, который записывает результат работы на левую полуленту и переходит в пассивное состояние.

3. Управляющее устройство начинает работу в состоянии .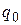

4. Если текущее состояние q не совпадает с одним из конечных состояний, то машина переходит в следующее состояние, определяемое согласно функции переходов. Пусть 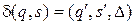, где s – считанный головкой символ из текущей ячейки. Тогда управляющее устройство переходит в состояние 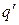, головка вместо символа s записывает символ 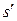и сдвигается на одну ячейку влево, если 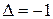, или вправо, если 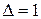. Затем, текущим становится состояние .

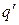5. Если 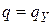, то вычисления заканчиваются с результатом “да”, если 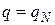, то – с результатом “нет”.

Временная сложность НДМТ-программы определяется равенством

.

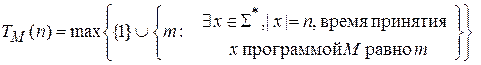(временная сложность угадывания считается за 1).

НДМТ-программа называется НДМТ-программой с полиномиальным временем работы, если существует полином некоторой степени k, такой что .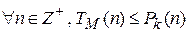

Класс языков NP формально определяется как

.

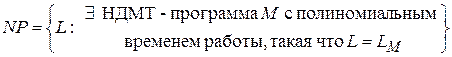Дата добавления: 2014-01-20