Передачи

Передачи – механизмы колёсного типа.

Назначение передач – преобразование и передача вращательного движения.

По характеру передачи движения передачи бывают следующих видов:

1. Передача движения за счёт сил трения:

a. Фрикционные передачи.

b. Ременные передачи.

2. Передача движения за счёт зацепления:

a. Зубчатые передачи.

b. Цепные передачи.

c. Передачи перфорированной лентой.

Конструктивно передачи делятся на следующие типы:

1. Передачи с непосредственным контактом:

a. Некоторые фрикционные передачи.

b. Зубчатые передачи.

2. Передачи с промежуточным звеном:

a. Некоторые фрикционные передачи.

b. Некоторые разновидности вариаторов.

c. Ременные передачи.

d. Цепные передачи.

e. Передачи перфорированной лентой.

Основной кинематической характеристикой всех передач является передаточное отношение.

Понятие о передаточном отношении и передаточном числе.

Передаточное отношение 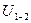– отношение угловых скоростей ведущего и ведомого звена, то есть .

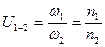Ведущее звено – звено, которое приносит энергию в передачу (ведущий вал, ведущее колесо).

Ведомое звено – вал или колесо, воспринимающее усилие от ведущего звена.

Ступень передачи – два колеса сопряжено работающих между собой с непосредственным сопряжением или с промежуточным звеном.

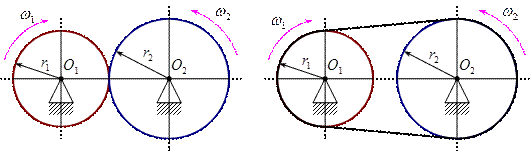
Различают две разновидности передачи по передаточному отношению:

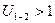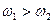1. Редуцирование , при . Назначение такой передачи – уменьшить число оборотов на ведомом звене по сравнению с ведущим.

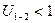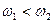2. Мультипликаторы , при . Назначение такой передачи - увеличить число оборотов на ведомом звене, по сравнению с ведущим.

Передача, играющая роль редуктора или мультипликатора выявляется только в общей схеме привода.

Рассмотрим двухступенчатый зубчатый механизм.

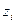- число зубьев на 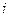-том зубчатом колесе.

I – редуктор.

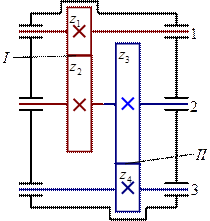II – мультипликатор.

Передаточное число 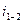- отношение числа оборотов быстроходного вала к числу оборотов тихоходного вала, то есть .

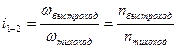В редукторах .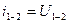

В мультипликаторах: .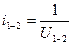

Понятие о «золотом» правиле в механике.

;

;

;

;

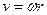
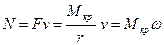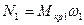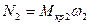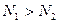, так как происходят потери при передаче.

Коэффициент полезного действия передачи 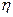– отношение мощности ведомого вала к мощности ведущего вала, то есть .

;

;

;

.

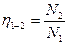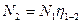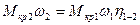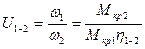Отношение угловых скоростей и крутящих моментов называют «золотым» правилом механики.

«Золотое» правило механики: если не учитывать коэффициент полезного действия, то отношение угловых скоростей обратно пропорционально отношению крутящих моментов.

.

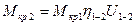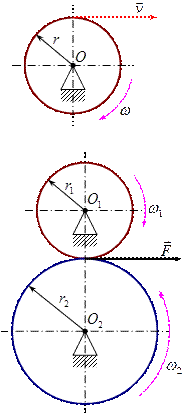
Фрикционные передачи.

Достоинства фрикционных передач:

1. Простота изготовления самих катков.

2. Возможность проскальзывания при перегрузках, что позволяет сохранить от поломок другие узлы машины связанные в кинематические цепи.

3. Возможность безступенчато менять передаточное отношение в передаче в пределах определённого диапазона регулирования (вариаторы).

Недостатки фрикционных передач:

1. Возможность проскальзывания, что не позволяет иметь стабильное передаточное отношение.

2. Громоздкость опор валов по сравнению с передачами зацепления.

Данная передача имеет название фрикционная передача с гладкими цилиндрическими катками. Кроме этой простой передачи бывают передачи клинчатыми цилиндрическими катками. Для передач с пересекающимися в пространстве осями применяются фрикционные передачи с коническими катками. Во всех перечисленных передачах передаточное отношение постоянно. Кроме того, существуют передачи с переменным передаточным отношением – вариаторы, у которых передаточное отношение 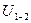меняется в пределах диапазона регулирования «».

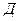Чтобы передать крутящий момент, нужно создать на границе силу трения, которая должна быть больше окружного усилия, то есть .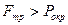

Для надёжности передачи окружного усилия вводится коэффициент надёжности 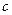, который для машинных передач равен 1.2-1.5, а для приборных передач – 2-5. С учётом этого 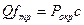. Нужно выполнить передачу окружного усилия 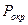. Задавшись коэффициентами надёжности и трения можно определить требуемое усилие: .

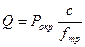Рассмотрим случай сухого трения, при котором 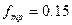, а коэффициент надёжности 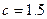, тогда .

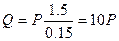Ширина катков определяется в зависимости от допускаемого удельного давления 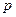на единицу длины линии контакта, соответствующая сопряжённым материалам. Таким образом: .

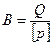Фрикционные передачи клинчатыми катками.

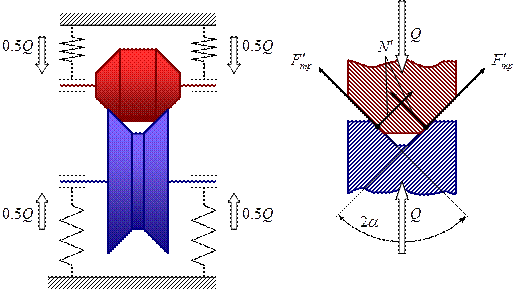
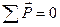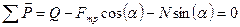Так как передача находится в равновесии, то сумма всех сил, действующих на ось равна нулю, то есть , или , где ; ; .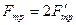

;

;

.

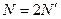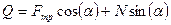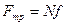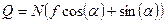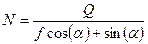Сила трения по окружности: 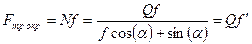, в которой 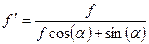- приведённый коэффициент трения. Анализируя приведённый коэффициент трения 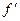, видно, что чем меньше угол 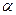, тем больше будет приведённый коэффициент трения 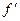. В передаче гладкими цилиндрами угол 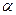равен девяносто градусам, поэтому коэффициент трения будет равен приведённому коэффициенту трения, то есть: 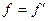. Так как в фрикционных передачах клинчатыми катками приведённый коэффициент трения больше коэффициента трения, то есть 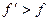, то сила .

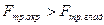Во всех фрикционных передачах имеет место упругое скольжение, то есть затрачивается некоторая энергия, переходящая в тепло за счёт относительного скольжения деформируемых сопряжённых поверхностей.

«Встреча» растянутых и сжатых участков на линии контакта 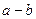во время работы передачи приводит к встрече противоположено деформированных участков, то есть от точки 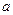до точки 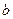на линии контакта неизбежно относительное скольжение поверхностей, что приводит к их нагреву и износу. Это имеет место во всех фрикционных передачах. Чем твёрже сопряженные поверхности, тем меньше линия контакта .

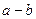Кроме того, в некоторых фрикционных передачах происходит геометрическое скольжение, например в передаче с клинчатыми катками.

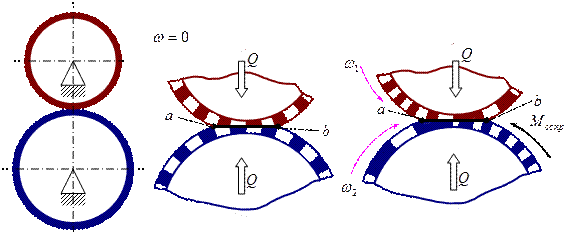
Понятие о геометрическом скольжении.

Примером геометрического скольжения могут служить фрикционные передачи с клинчатыми катками.

Допустим, что на линии контакта 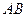есть некоторая точка 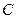, на которой скорости обоих колёс одинаковы, то есть 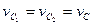. На самой линии контакта 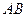, на всём её протяжении, кроме точки 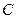, линейные скорости колёс различны, то есть 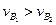и 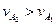. Таким образом, везде происходит относительное скольжение, что приводит к нагреву и износу сопряжённых конусных поверхностей, что, в свою очередь, понижает коэффициент полезного действия передачи. Чтобы избежать этого не следует делать общую образующую 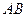больших размеров. Необходимо уметь находить оптимальный размер образующей .

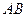Явление, где на сопряжённых поверхностях векторы линейных скоростей в одних и тех же точках различны, что связано с геометрией формы, принято называть геометрическим скольжением. Его следует избегать, однако это не всегда удаётся.

Фрикционные передачи с коническими катками.

Назначением фрикционных передач с коническими катками является преобразование вращательного движения между пересекающимися в пространстве осями.

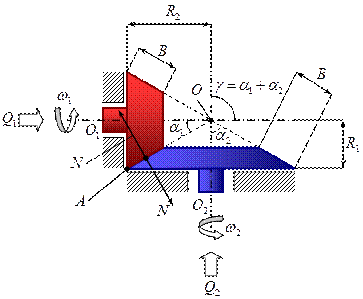
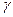- угол между осями вращения.

Передаточное отношение: .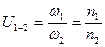

Допустим, что в некоторой точке 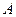выполняется услови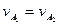е: , где , 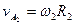. Тогда 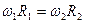или .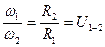

Рассмотрим два треугольника 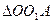и :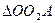

; ;

; ;

.

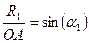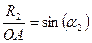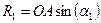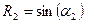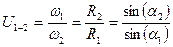Как следует из последнего выражения, передаточное отношение в передаче с коническими катками выражается через тригонометрические функции, то есть выбранное нами положение точки 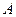на общей образующей 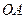безразлично, то есть на всём протяжении образующей 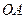в точках контакта линейные скорости одинаковы, то есть происходит чистое обкатывание без скольжения.

Это справедливо только для случая, когда общая образующая проходит через точку пересечения осей вращения катков. Если это условие нарушается, то появляется геометрическое скольжение.

Понятие о начальной окружности.

На каждом зубчатом колесе, сопряжено работающем в паре, обязательно есть такие окружности, которые обкатываются одна по другой без скольжения. Такими окружностями являются окружности, сопрягаемые в полюсе зацепления. Эти окружности называются начальными окружностями.

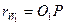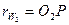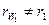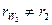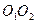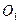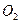В нашем случае это окружности и . Если колёса не корректированы, то начальные окружности совпадают с делительными. Если колёса в передаче корректированы, то и . При корректировании могут быть исправлены межцентровое расстояние . Центры и могут быть разведены или сближены, в зависимости от требований. В таких колёсах постоянными остаются диаметры делительных окружносте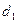й и , и появляются диаметры начальных окружностей и .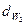

На отдельно взятом колесе отсутствует начальная окружность, она появляется только в процессе сопряжено работающих колёс.

На зубчатом колесе следует различать пять окружностей:

1. Делительная окружность .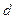

2. Начальная окружность 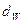(в сопряжённой передаче).

3. Основная окружность 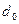(окружность от которой строится эвольвента).

4. Окружность выступов .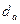

5. Окружность впадин .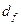

Основные понятия и определения из теории зацепления.

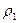
и 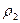- радиусы основных окружностей.

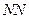- общая касательная к основным окружностям.

Изобразим сопряжённые профили у полюса зацепления. Так как линия 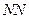является общей касательной к основным окружностям, то, исходя из геометрии построения эвольвенты, профили зубьев всегда будут касаться только на этой линии. Линия 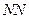всегда будет перпендикулярна к сопряжённым профилям. Поэтому линию 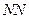принято называть линией зацепления.

Линия зацепления – геометрическое место точек контакта двух сопряжено работающих профилей.

На линии 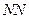различают теоретический и рабочий участки линии зацепления.

Теоретический участок – отрезок между основаниями перпендикуляров, опущенных на линию зацепления 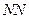из центров.

Практический или рабочий участок – участок линии зацепления, ограниченный внешними окружностями колёс.

Если за пределами теоретического участка частично окажется рабочий участок, то нарушится постоянство передаточного соотношения. Чтобы передаточное отношение было постоянным необходимо, чтобы рабочий участок находился в пределах теоретического.

Изобразим профили зубьев в момент встречи и расставания, и отметим на начальной окружности положение профилей при встрече и расставании. Дуга 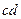на начальной окружности есть путь 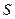в процессе контакта. Дуга 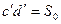- дуга зацепления на основной окружности.

Коэффициент перекрытия 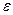- коэффициент, показывающий количество шагов, укладывающихся в дуге зацепления, .

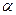- угол зацепления. Угол зацепления гостирован, так как положение нормали определяет кривизну профиля.

Коэффициент перекрытия оптимален, если он больше единицы. Чем больше коэффициент перекрытия 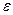, тем лучше работает передача, то есть улучшается плавность зацепления. Если коэффициент перекрытия меньше единицы, то встречи и расставания зубьев будут сопровождаться ударами.

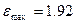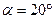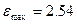при ; при .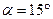

Численное значение коэффициента перекрытия 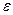показывает количество пар зубьев, одновременно находящихся в зацеплении. Если 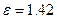, то в процессе зацепления 42 процента времени в контакте между колёсами находится две пары зубьев, а остальные 58 процентов времени контакт между колёсами осуществляется только одной парой зубьев.

В технике более распространены передачи с углом зацепления 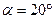, поскольку габариты передачи в этом случае получаются меньше, чем при угле зацепления .

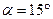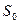
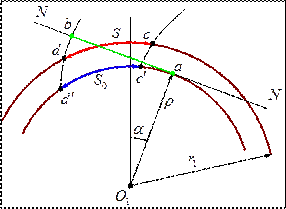- дуга зацепления на основной окружности.

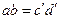, так как 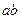является развёрткой дуги .

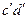Соотношение между длинами дуг и радиусами:

;

;

.

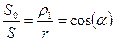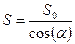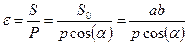Выше приведённым образом определяется значение коэффициента перекрытия 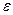. Если коэффициент перекрытия 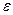больше единицы, то шаг 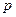будет больше, чем дуга зацепления 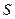и передача будет работать с ударами.

Сравним коэффициенты перекрытия косозубой и прямозубой передач: 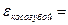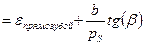, где 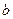- ширина венца зубчатого колеса, 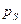- шаг зацепления в торцевом сечении колеса.

Косозубая конструкция позволяет довести коэффициент перекрытия до 8-10.

Геометрические параметры косозубых зубчатых колёс.

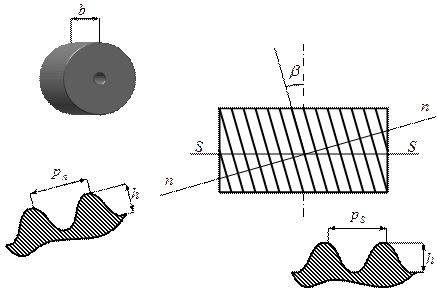
В косозубом зубчатом колесе различают шаг и модуль зацепления в нормальном по отношению к зубу сечении 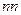и в торцевом сечени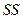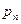и - и 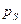соответственно. При этом выполняется условие: 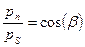, или 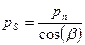. Так как шаг зацепления пропорционален модулю зацепления, то , то есть 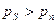, где 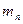- стандартная величина.

Диаметр окружности выступов: 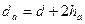, где ;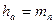

; .

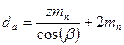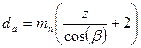Диаметр окружности впадин: 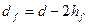, где ;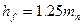

; .

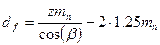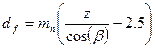При расчётах на прочность зубьев косозубых колёс пользуются формулами для расчёта прямозубых цилиндрических колёс. Это допускается, если представить себе зуб косозубого колеса, как зуб, принадлежащий некоторому цилиндрическому прямозубому колесу. Такое колесо отличается от косозубого числом зубьев. Его принято называть приведённым или эквивалентным. Определим число зубьев эквивалентного прямозубого колеса. Это нужно знать при расчете зуба на изгиб. Коэффициент формы зуба 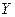берётся в зависимости от числа зубьев.

;

;

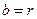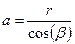Рассмотрим околополюсное состояние зацепления. Зубья в полученном сечении располагаются, как около начальной окружности некруглого колеса.

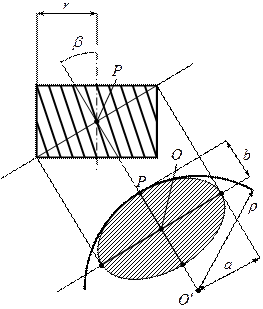
Представим себе околополюсное состояние в виде цилиндра, имеющего радиус кривизны, соответствующий точке 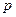на эллипсе: 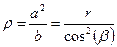. Диаметр этой окружности, равный 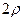будет являться диаметром эквивалентного цилиндрического колеса.

Определим число зубьев приведённого колеса :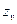

;

.

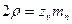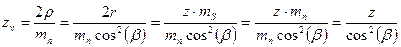То есть число зубьев приведенного колеса больше числа зубьев данного косозубого колеса: .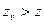

Дата добавления: 2014-01-20