
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
A) элементтері болса 4 страница
|
|
|
|
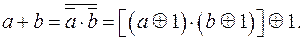 (1.14)
(1.14)
Справедливость (1.13) проверяется с помощью таблицы истинности для операции «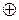 » (сложение по mod 2). Формула (1.14) выводится на основании (1.6) с использованием (1.13).
» (сложение по mod 2). Формула (1.14) выводится на основании (1.6) с использованием (1.13).
Пример 1.6.6.
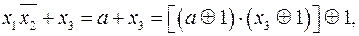
где 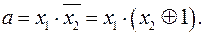
1.6.7. Таблица формул преобразования
базиса {И, ИЛИ, НЕ}.
| Таблица 1.6.2 | |
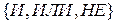 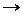 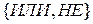
| 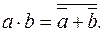
|
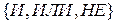 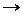 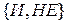
| 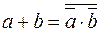
|
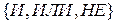 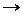 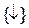
| 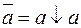
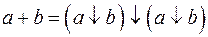
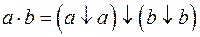
|
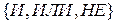 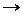 { / }. { / }.
| 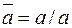
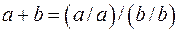
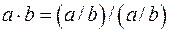
|
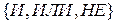 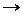 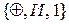
| 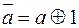
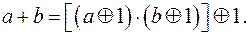
|
Каждый базис логических операций по сути дела есть начало для создания соответствующей частной алгебры логики. Так, например, базис 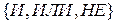 положен в основу так называемой булевой алгебры. Поводом к её созданию послужили работы английского математика Дж. Буля, датированные серединой девятнадцатого столетия. Вполне достаточно условий (наличие множества переменных и набора операций над ними) для образования алгебр на основе базисов
положен в основу так называемой булевой алгебры. Поводом к её созданию послужили работы английского математика Дж. Буля, датированные серединой девятнадцатого столетия. Вполне достаточно условий (наличие множества переменных и набора операций над ними) для образования алгебр на основе базисов 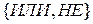 и
и 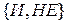 . Практическое значение имеют алгебра Шеффера (базис { / }) и алгебра Пирса (базис
. Практическое значение имеют алгебра Шеффера (базис { / }) и алгебра Пирса (базис 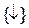 ). Специализированной в прикладном значении является алгебра Жегалкина (базис
). Специализированной в прикладном значении является алгебра Жегалкина (базис 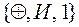 ).
).
Отмеченные выше частные алгебры не являются единственно возможными. В принципе, имеют право на существование алгебры для каждого базиса представленного в таблице 1.6.1. Но, упомянутые алгебры выделяются среди остальных некоторыми отличительными особенностями, которые позволяют обеспечить выполнение заданных целей при формировании логических функций.
Отличительная особенность алгебры Шеффера и Пирса состоит в возможности выразить любую логическую функцию, используя только одинаковые операции. В прикладном плане данная особенность позволяет унифицировать элементы технических устройств, реализующих заданные логические функции. Алгебра Жегалкина даёт теоретическую основу для построения вычислительных средств, реализующих арифметические операции в двоичной системе счисления. Но, абсолютное первенство при реализации задач практики занимает булева алгебра. Ей свойственна простота (конечно, относительно других алгебр) различного рода преобразований логических функций. Более привычное визуальное восприятие функций (особенно при обозначении дизъюнкции и конъюнкции знаками «+» и «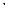 »). В подавляющем большинстве случаев записи булевых функций содержат меньшее число операций и, поэтому, имеют более компактное описание. Подтверждением тому служит пример 1.6.7.
»). В подавляющем большинстве случаев записи булевых функций содержат меньшее число операций и, поэтому, имеют более компактное описание. Подтверждением тому служит пример 1.6.7.
Пример 1.6.7.
Пусть задана булева функция 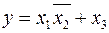 . Дляпредставления её в других алгебрах воспользуемся формулами преобразования из
. Дляпредставления её в других алгебрах воспользуемся формулами преобразования из
таблицы 1.6.2.
1. Преобразование в алгебру Шеффера (базис { / }).
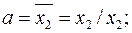
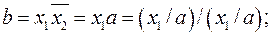

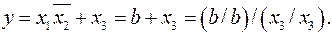
Если значение  подставить во второе равенство, а значение
подставить во второе равенство, а значение 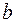 – в 3-е равенство, получим окончательный результат.
– в 3-е равенство, получим окончательный результат.
2. Преобразование в алгебру Пирса (базис 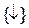 ).
).
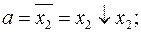
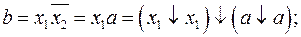
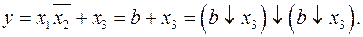
Проделаем подстановки аналогичные предыдущему пункту и получим требуемый результат.
2. Преобразование в алгебру Жегалкина (базис 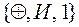 ).
).
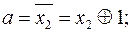
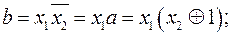
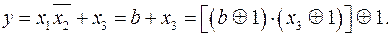
Так же как и в первых двух пунктах сделаем подстановки для получения искомого результата.
В результате указанных подстановок во всех трёх пунктах примера 1.6.7 получаются громоздкие представления функций. Правда, в некоторых случаях существует возможность их упрощения (минимизации). Упрощение есть целевое преобразования функций с целью уменьшения числа операций а, возможно, и сокращения состава её переменных. Такая процедура не всегда приводит к успеху. Взвесив всё за и против, инженерная практика применения различных частных алгебр отдаёт предпочтение булевой алгебре. 
Все прикладные вопросы использования алгебры логики в основном базируются на булевой алгебре. Ей уделяется большое внимание в специальной литературе. Её надо хорошо знать инженеру, занимающемуся вопросами проектирования логических и цифровых систем управления промышленными объектами. Поэтому всё дальнейшее описание посвящается булевой алгебре. Некоторые отступления от этого будут оговариваться особо.
2. БУЛЕВА АЛГЕБРА
2.1. Аксиомы и законы булевой алгебры
В основе алгебры лежат девять аксиом.
1. 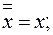

| 2. 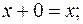 3.
3. 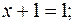 4.
4. 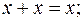 5.
5. 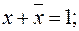
| 6. 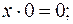 7.
7. 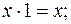 8.
8. 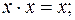 9.
9. 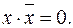
|
Истинность аксиом подтверждается путем подстановки значений логической переменной 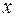 в их аналитическое представления. Так, для первой аксиомы
в их аналитическое представления. Так, для первой аксиомы
при 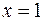 имеет место
имеет место 
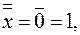
при 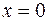 имеет место
имеет место 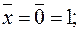
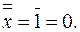
| Таблица 2.1.1. | ||
| X | Y | Z |
В обоих случаях имеет место подтверждение первой аксиомы. Вторая, третья, четвёртая и пятая аксиомы проявляется при анализе таблицы истинности для операции «ИЛИ». Для аналитической формы этой операции 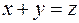 соответствует таблица 2.1.1. При
соответствует таблица 2.1.1. При 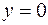 (первая и третья строчки таблицы) всегда
(первая и третья строчки таблицы) всегда 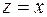 . Следовательно, всегда
. Следовательно, всегда 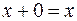 , что и требовалось показать. Истинность остальных аксиом демонстрируется точно таким же образом.
, что и требовалось показать. Истинность остальных аксиом демонстрируется точно таким же образом.
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 449; Нарушение авторских прав?; Мы поможем в написании вашей работы!