Решение

1. Найдём длину ребра .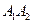

Найдём векторы .

.

.

.

.

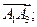
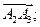
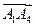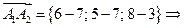
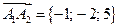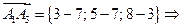
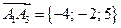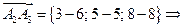
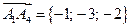Найдём модуль вектора 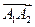(длину ребра ).

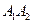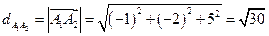единиц длины.

2. Найдём угол между ребрам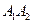и и .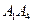

Угол между рёбрам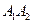и и 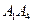найдём как угол между векторам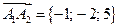и

и 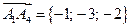через скалярное произведение векторов.

, .

.

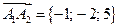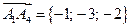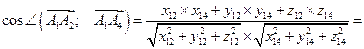
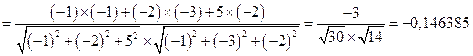Следовательно, угол между ребрам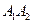и и 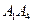, равен

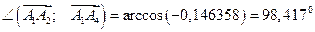
3. Найдём площадь грани .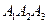

Выше нашли векторы:

.

.

.

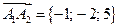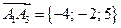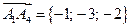То есть, имеем векторы:

.

,

.

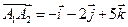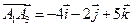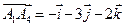Найдём векторное произведение векторов 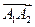и .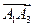

.

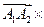
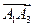
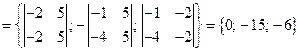Модуль векторного произведения равен:

.

Площадь грани 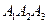равна:

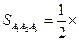
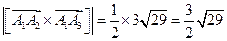единиц площади.

4. Найдём объем пирамиды .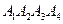

Выше нашли:

, , .

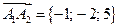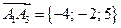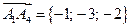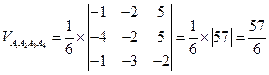единица объёма.

5. Найдём уравнение плоскости .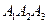

Составим уравнение плоскости, проходящей через точки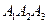

.

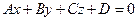В общем случае для точек 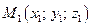, , 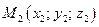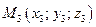искомое уравнение плоскости определяется условием

.

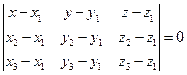В нашем случае для точек 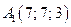, , 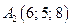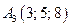получим

.

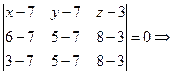
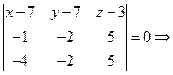
6. Найдём нормальный вектор плоскости .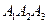

Выше нашли уравнение плоскости, проходящей через точки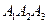

.

Нормирующий множитель имеет вид

.

Знак нормирующего множителя выбирается противоположно знаку свободного члена .

Тогда,

.

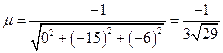Вычислим направляющие углы перпендикуляра к данной плоскости.

.

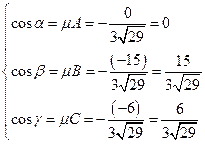Нормальный вектор к плоскости 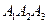можно записать в виде:

.

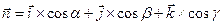Тогда, искомый вектор есть

.

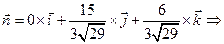
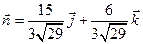7. Найдём уравнение прямой линии, походящей через точку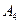

перпендикулярно плоскости .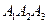

Уравнение плоскости нашли выше

.

.

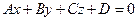Имеем точку .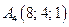

Пусть искомое уравнение имеет вид:

.

В нашем случае получим

.

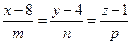Условие перпендикулярности прямой и плоскости есть

.

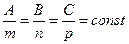Положим

.

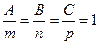Тогда,

.

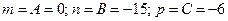Следовательно, искомое уравнение прямой, проходящей через точку 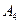перпендикулярно плоскости 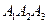имеет вид

.

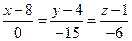СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.

1. Высшая математика для экономистов: Учебник для ВУЗов/Под ред. Н.Ш Кремера. – М.: ЮНИТИ, 2001. – 472 с.

2. Кириллов А.Л. Математика для управленцев: Курс лекций. – СПб., 2000. – 240 с.

3. Ибатуллина С.М. Математика. Учебно-методический комплекс. –Уфа, БАГСУ, 2007. - 91 с.

4. Ефимов А.В., Демидович Б.П. Сборник задач по математике для втузов: линейная алгебра и основы математического анализа. – М.: Наука, 1981, 1986, ч.ч. 1,2,3.

5. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1978.

6. Карасев А.И., Аксютина З.М., Савельева Т.М. Курс высшей математики для экономических вузов. – М.: Высшая школа, 1982.

7. Рабочая тетрадь по высшей математике «Элементы линейной алгебры и комплексные числа». Ч.1. – Уфа: РИО БАГСУ, 2000. – 25 с.

8. Высшая математика для экономистов: Учебник для ВУЗов/Под ред. Н.Ш Кремера. – М.: ЮНИТИ, 2001. – 472 с.

9. Кириллов А.Л. Математика для управленцев: Курс лекций. – СПб., 2000. – 240 с.

10. Ефимов А.В., Демидович Б.П. Сборник задач по математике для втузов: линейная алгебра и основы математического анализа. – М.: Наука, 1981, 1986, ч.ч. 1,2,3.

11. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1968.

12. Карасев А.И., Аксютина З.М., Савельева Т.М. Курс высшей математики для экономических вузов. – М.: Высшая школа, 1982.

13. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1986.

14. Ибатуллина С.М. Математика. Учебно-методический комплекс. –Уфа, БАГСУ, 2007. - 91 с.

15. Рабочая тетрадь по высшей математике «Элементы векторной алгебры и аналитической геометрии». Ч.2. – Уфа: РИО БАГСУ, 2000. – 32 с.

Дата добавления: 2014-11-16