Случай 4

Пусть система ограничений ЗЛП представлена в виде:

(),

()

().

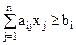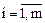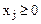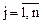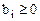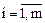Приведем систему к каноническому виду. Для этого вычтем из левых частей неравенств новые неотрицательные переменные.

(),

()

().

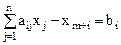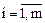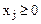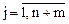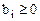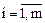Переменные 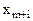(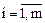) не являются предпочтительными. Случай 4 свелся к случаю 3.

Рассмотрены всевозможные варианты составления начального опорного плана. Однако, следует отметить, что на практике чаще всего встречаются смешанные системы ограничений, т.е. системы где есть уравнения, содержащие предпочтительную переменную, не содержащие таковую, неравенства. Для каждого ограничения такой системы находится своя предпочтительная переменная.

Пример 3: Составить начальный опорный план при решении ЗЛП:

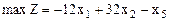
при

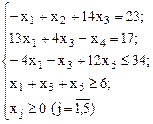
Решение.

Первое уравнение системы имеет предпочтительный вид (случай 1). Предпочтительная переменная 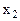. Второе уравнение не содержит предпочтительной переменной (случай 2). Необходимо добавить одну переменную искусственного базиса 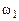. Получим уравнение:

.

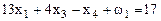В целевую функцию новая переменная войдет с коэффициентом, равным –М.

Третье ограничение имеет вид неравенства ≤ (случай 2). Необходимо добавить дополнительную переменную 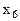. Она и будет иметь предпочтительный вид. В целевую функцию она войдет с коэффициентом 0.). Следовательно, вычтем из левой части неравенства 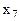и добавим вторую переменную искусственного базиса 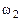. Соответственно, в целевую функцию добавятся две новые переменные с коэффициентами 0 и –М соответственно.

Таким образом, ЗЛП будет иметь следующий вид:

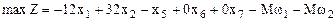
при

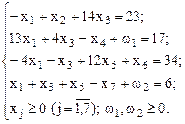
Базис системы составляют переменные: 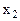, , 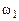, 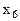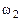(представлены в соответствии с уравнениями, предпочтительными переменными которых являются данные переменные). Следовательно, начальный опорный план ЗЛП имеет вид: (0, 23, 0, 0, 0, 34, 0, 17, 6).

Замечание: При составлении начального опорного плана для данной задачи учитывались все новые переменные в следующей последовательности: сначала переменные 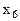и 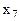, а затем 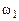и .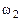

2.6. Признак оптимальности опорного плана. Симплексные таблицы

Для того, чтобы было удобнее решать ЗЛП симплексным методом были придуманы симплексные таблицы, которые позволяют максимально алгоритмизировать процесс решения задачи линейного программирования. Симплексная таблица составляется только в том случае, если составлен начальный опорный план.

Пусть ЗЛП представлена в каноническом виде:

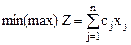
при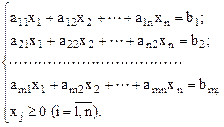

С помощью метода Гаусса (см. 1.12) преобразуем систему ограничений и приведем ее к следующему виду:

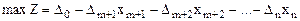
при

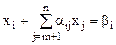(i= )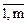

Из записи ЗЛП видно, что первые m переменных являются базисными. При этом мы не нарушаем общности рассуждений, так как то, что базисными будут первые m переменных, позволит более наглядно проиллюстрировать теорию.

Составим симплексную таблицу:

БП	СБ	А			…			…		…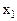
		…			…		…
					…			…		…
					…			…		…
…	…	…	…	…	…	…	…	…	…	…	…
					…			…		…
…	…	…	…	…	…	…	…	…	…	…	…
					…			…		…
				…			…		…

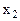
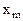
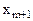
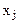
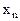
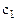
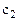
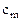
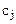
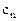
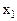
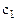
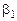
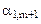
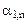
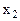
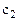
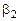
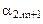
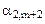
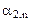
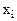
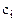
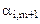
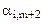
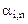
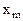
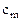
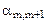
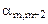
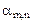
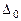
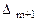
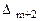
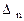
В первом столбце (БП) пишутся базисные переменные. Все базисные переменные пишутся В СООТВЕТСТВИИ С УРАВНЕНИЯМИ, ДЛЯ КОТОРЫХ ДАННЫЕ ПЕРЕМЕННЫЕ ЯВЛЯЮТСЯ ПРЕДПОЧТИТЕЛЬНЫМИ.

Во втором столбце (СБ) пишутся коэффициенты для соответственных базисных переменных в целевой функции.

В третьем столбце (А) пишутся свободные члены в уравнениях системы ограничений.

В первой строке после обозначения первых трех столбцов (БП, СБ, А) пишутся все переменные, которые есть в ограничениях, включая дополнительные и искусственные. Порядок следования переменных неизменен. под каждой переменной пишется ее коэффициент в целевой функции.

В таблице со второй строки четвертого столбца пишутся все коэффициенты соответственных переменных в системе ограничений.

В последней строке пишутся оценки. Оценки считаются по формулам (см. 1.12):

…………………………………….

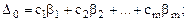
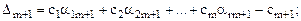
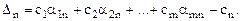
Оценки для базисных переменных равны 0.

Замечание: Оценки считаются как скалярное произведение соответственного столбца на столбец СБ минус коэффициент в целевой функции для данной переменной.

Последнюю строку называют индексной строкой симплексной таблицы. Значение 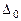– значением целевой функции для данного начального опорного плана, а все остальные Δ – оценками свободных переменных.

Теорема 1: (признак оптимальности опорного плана при решении задач на максимум) Пусть исходная ЗЛП решается на максимум. Если для некоторого опорного плана в индексной строке симплексной таблицы все оценки 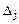(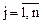) неотрицательны, то такой план будет оптимальным.

Теорема 2: (признак оптимальности опорного плана при решении задач на минимум) Пусть исходная ЗЛП решается на минимум. Если для некоторого опорного плана в индексной строке симплексной таблицы все оценки 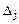(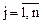) неположительны, то такой план будет оптимальным.

Пример 1: Составить симплексную таблицу и посчитать оценки для задачи линейного программирования вида:

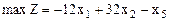
при

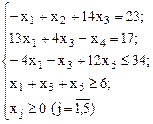
Решение.

Построение начального опорного плана рассмотрено в 2.5.

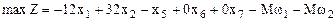
при

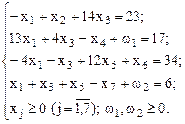
Базис системы составляют переменные: 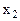, , 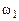, 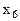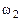(представлены в соответствии с уравнениями, предпочтительными переменными которых являются данные переменные).

БП	СБ	А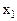
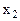
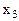
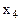
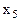
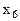
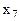
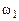
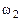
-12				-1			–M	–M
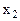
			-1
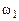
	–M					-1
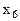
			-4		-1
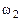
	–M								-1
св. чл		-20
M	-23	-14		-5		-1

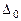=23∙32-17 M+0∙34-6∙M=-23∙M+736;

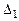=-1∙32-13∙M-0∙4-1∙M+12=-14∙M-20;

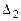=32∙1-0∙M+0∙0-0∙M-32=0∙M+0=0 (базисная переменная);

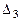=32∙14-4∙M-0∙1-1∙M-0=-5∙M+448;

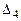=32∙0+1∙M+0∙0-0∙M-0=1∙M+0;

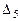=32∙0-0∙M+0∙12-1∙M+1=-1∙M+1;

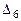=32∙0-0∙M+0∙1-0∙M-0=0∙M+0=0 (базисная переменная);

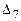=32∙0-0∙M+0∙0+1∙M-0=1∙M+0=0;

=32∙0-1∙M+0∙0-0∙M+M=0∙M+0=0 (базисная переменная);

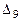=32∙0-0∙M+0∙0-1∙M+M=0∙M+0=0 (базисная переменная);

Для данного начального опорного плана ответ: Z=-23∙M+736 при (0, 23, 0, 0, 0, 34, 0, 17, 6).

Замечание: Значение Z взято из индексной строки симплексной таблицы (пересечение индексной строки и столбика А). Значение базисных переменных из столбика А.

Данный опорный план не является оптимальным, т.к. в индексной строке симплексной таблицы есть отрицательные оценки, соответствующие свободным переменным.

2.7. Переход к нехудшему опорному плану.

Пусть решается ЗЛП с системой ограничений в предпочтительном виде:

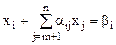(i= )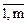

Начальный опорный план для такой задачи: 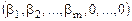. Значение целевой функции: Z= .

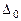Пусть исходная задача решается на максимум (для ЗЛП на минимум все рассуждения аналогичны). Если все оценки 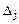(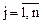) неотрицательны, то план оптимален и задача решена. Предположим, что среди оценок свободных членов есть по крайней мере одна отрицательная. Обозначим ее 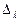. Назовем соответственный вектор столбец 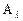- разрешающим, а соответственную переменную 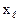- перспективной.

Попытаемся заменить некоторую базисную переменную на 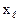. При этом все остальные свободные переменные не должны измениться.

Рассмотрим систему ограничений ЗЛП:

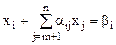(i= )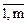

Преобразуем ее следующим образом:

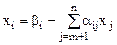(i= )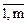

Так как все свободные переменные кроме 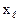равны 0, получим:

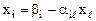(i= 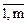) (1).

Отсюда:

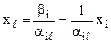(i= ).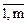

По условию задачи линейного программирования все переменные, включая 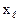, должны быть неотрицательны. Следовательно:

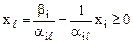(i= ).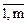

Отсюда:

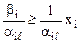(i= ).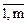

Так как базисных переменных не может быть больше m, то при внесении в базис 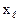какая-то из базисных переменных будет свободной. Пусть это переменная 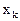. Тогда:

→

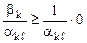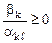
По условию задачи все - неотрицательны. Тогда и 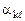должно быть положительным.

Таким образом, базисный элемент 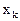и соответственную строку k следует искать среди строк, которых положительны.

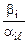Не ограничивая общности, предположим, что первые s строк имеют >0. Найдем отношение для всех этих строк. Получим последовательность чисел 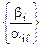. Среди чисел этой последовательности выберем минимальное:

min 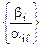= =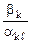Θ.

Назовем это отношение наименьшим симплексным отношением. Соответствующий элемент 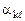– разрешающим и соответственную строку k – разрешающей. Базисная переменная 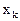будет считаться неперспективной.

Вернемся к равенству (1).

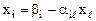(i= 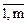) (1).

Для i=k получим:

.

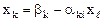Отсюда:

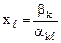= Θ

Тогда:

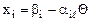(i= ).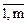

Новый базис будет состоять из переменных 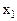, , 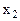…, , , , 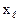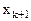…, 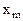. Соответствующий ему опорный план имеет вид:

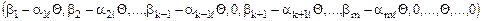
Проверим, является ли полученный опорный план "нехудшим". Для этого найдем 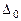для нового опорного плана:

,

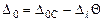где 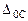– значение целевой функции первоначального опорного плана, 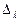- оценка, соответствующая столбцу 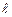. Так как 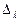<0, а Θ>0, то полученное значение целевой функции >

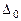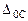
Алгоритм выбора разрешающего элемента для задач линейного программирования на максимум (минимум) представлен на Рис. 12.

2.8. Симплексные преобразования

Для того, чтобы перейти к новому базису необходимо выразить новую базисную переменную через свободные переменные.

Рассмотрим систему ограничений ЗЛП:

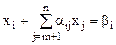(i= )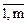

Рис. 12. Алгоритм выбора разрешающего элемента для задач линейного программирования на максимум (минимум)

Преобразуем ее следующим образом:

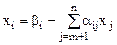(i= )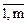

Выразим из системы базисную переменную :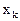

.

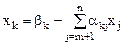Распишем подробнее:

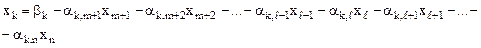
Отсюда:

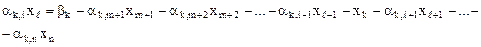
Тогда

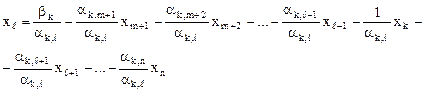
Подставим данное равенство в другие ограничения системы:

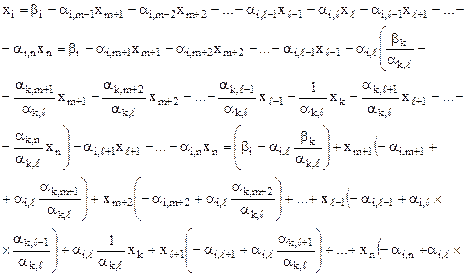
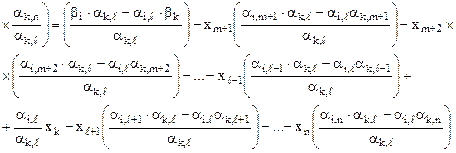
Для целевой функции формула представима в виде:

Вычисление по данным формулам получило название симплексных преобразований. Для того чтобы перейти с помощью симплексных преобразований к новому опорному плану можно действовать двумя способами.

Дата добавления: 2014-11-18