
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бор постулаттары
|
|
|
|
Дания ғалымы Бор Резерфорд моделіндегі кемшіліктерді түсіндіріп беретін келесі постулаттарды ұсынды:
Бордың бірінші постулаты (стационар күйлер постулаты):
Атом белгілі бір тұрақты дискретті күйлерде болады. Бұл күйдегі атом сәуле шығармайды және жұтпайды.
Импульс моментінің квантталу ережесі. Атомдағы электронның импульс моменті тек белгілі бір дискретті мәндерді қабылдайды, яғни квантталады.

Бордың екінші постулаты (жиіліктер ережесі):
Атом бір тұрақты күйден екіншісіне өткенде сәуле шығарады немесе жұтады.
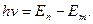
1) 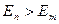 болғанда атом сәуле шығарады.
болғанда атом сәуле шығарады.
2) 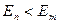 болғанда атом сәуле жұтады.
болғанда атом сәуле жұтады.
31.5.Бор теориясын сутегі атомына қолдану
Сутегі атомында электрон ядроның айналасында Кулондық тартылу күшінің әсерінен радиусы 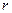 -ге шеңберлік орбитамен қозғалады. Сондықтан электонды осы орбитада ұстап тұратын центрге тартқыш күш электрон мен ядро арасындағы Кулондық күшке тең болады:
-ге шеңберлік орбитамен қозғалады. Сондықтан электонды осы орбитада ұстап тұратын центрге тартқыш күш электрон мен ядро арасындағы Кулондық күшке тең болады:
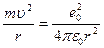 .
.
Импульс моментінің квантталу ережесін ескерсек, алатынымыз:
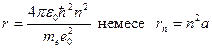 ,
,
мұндағы: 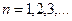
Сутегі атомындағы электронның орбитасы тек дискретті мәндерді қабылдайды, яғни квантталады.
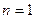 тең болғанда сутегі атомындағы электронның бірінші орбитасының мәні алынады:
тең болғанда сутегі атомындағы электронның бірінші орбитасының мәні алынады: 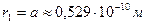 . Бұл мән бірінші Бор радиусы деп аталады.
. Бұл мән бірінші Бор радиусы деп аталады.
Сутегі атомының стационар күйінің энергиясы:
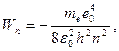
мұндағы: 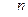 -бас кванттық сан. Бас кванттық сан атом энергиясының деңгейін анықтайды. n=1 атомның негізгі күйі, n>1 атомның қозған күйі деп аталады.
-бас кванттық сан. Бас кванттық сан атом энергиясының деңгейін анықтайды. n=1 атомның негізгі күйі, n>1 атомның қозған күйі деп аталады.
Сутегі атомының энергиясы тек дискретті мәндерді қабылдайды, яғни квантталады.
31.6.Франк және Герц тәжірибесі
Неміс ғалымдары Франк және Герц Бор теориясын дәлелдейтін келесі тәжірибе жасады. Олар төменгі қысымдағы сынап буы толтырылған ыдыстағы үш электродты лампа – триод көмегімен тәжірибе жасады. Электрондардың сынап атомдарымен серпімсіз соқтығысы кезінде электроннан атомға энергия беріледі және бұл энергия жеке дискретті порциялар түрінде беріледі. Бұл тәжірибеден шығатын қортынды: атом энергиясы тек дискретті мәндерді қабылдайды және атомның шығаратын сәулелік энергиясы осы энергиялық күйлердің айырмасына тең.
Сутегі атомы үшін Шредингер теңдеуі келесі түрде жазылады:
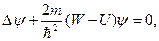
мұндағы: 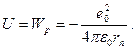
Сутегі атомындағы электронның күйі берілген стационар Шредингер теңдеуін қанағаттандыратын 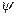 -толқындық функциямен сипатталады.
-толқындық функциямен сипатталады.
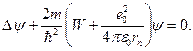
Сутегі атомы үшін Шредингер теңдеуінің сфералық координаттағы шешімінен атомдағы электронның импульс моменті тек дискретті мәндерді қабылдайтыны, яғни квантталатыны шығады.
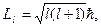
мұндағы: 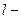 орбитальдық кванттық сан,
орбитальдық кванттық сан, 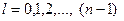
Орбитальдық кванттық сан атомның импульс моментінің мәнін анықтайды.
Орбитальдық кванттық санның мәніне байланысты электрон күйлерін келесі түрде атайды:
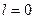 болғанда
болғанда 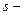 электрон,
электрон,
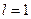 болғанда
болғанда 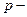 электрон,
электрон,
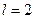 болғанда
болғанда 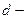 электрон,
электрон,
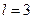 болғанда
болғанда 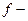 электрон.
электрон.
31.7.Кеңістіктік квантталу
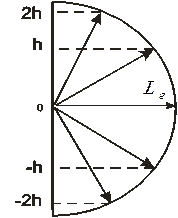
| Электронның 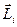 орбиталық импульс моментінің сыртқы магнит өрісі бағытындағы орбиталық импульс моментінің сыртқы магнит өрісі бағытындағы 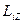 проекциясы тек белгілі мәндерді қабылдайды, яғни квантталады. проекциясы тек белгілі мәндерді қабылдайды, яғни квантталады.
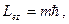 мұндағы:
мұндағы: 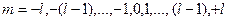 -
магниттік кванттық сан. Соныменен -
магниттік кванттық сан. Соныменен 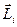 векторы кеңістікте векторы кеңістікте 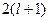 бағыт қабылдай алады. бағыт қабылдай алады.
|
Магниттік кванттық сан 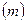 сыртқы магнит өрісінің бағытындағы орбитальдық импульс моментінің проекциясын анықтайды.
сыртқы магнит өрісінің бағытындағы орбитальдық импульс моментінің проекциясын анықтайды.
Электронның меншікті 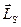 импульс моментін спин деп атайды. Электронның спині (кез-келген бөлшектің) оның массасы, заряды сияқты оның негізгі сипаттамасы болып табылады. Кванттық механика заңдылықтарынан электронның спині келесі заң бойынша квантталатыны шығады:
импульс моментін спин деп атайды. Электронның спині (кез-келген бөлшектің) оның массасы, заряды сияқты оның негізгі сипаттамасы болып табылады. Кванттық механика заңдылықтарынан электронның спині келесі заң бойынша квантталатыны шығады:
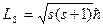 ,
,
мұндағы: 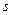 - спиндік кванттық сан.
- спиндік кванттық сан.
Спиннің 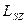 сыртқы магнит өрісінің бағытымен сәйкес келетін
сыртқы магнит өрісінің бағытымен сәйкес келетін 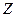 -осіндегі проекциясы квантталады және
-осіндегі проекциясы квантталады және 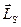 векторының магнит өрісінде әр түрлі
векторының магнит өрісінде әр түрлі 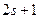 бағыты болады. Штерн және Герлах тәжірибесі көрсеткендей, электрон үшін мұндай бағыт екеу болады.
бағыты болады. Штерн және Герлах тәжірибесі көрсеткендей, электрон үшін мұндай бағыт екеу болады.
Спиндік кванттық санның басқа үш кванттық сандардан- 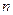 бас,
бас, 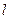 орбитальдық және
орбитальдық және 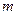 магниттік кванттық сандардан ерекшелігі, ол бүтін сан болмайды.
магниттік кванттық сандардан ерекшелігі, ол бүтін сан болмайды.
Электрон үшін спиннің сандық мәні келесі формуламен анықталады:
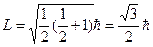 .
.
Кеңістіктік квантталуға сәйкес электронның меншікті импульс моменті 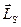 векторының сыртқы магнит өрісі бағытындағы
векторының сыртқы магнит өрісі бағытындағы 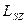 проекциясы да квантталады:
проекциясы да квантталады:
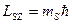 ,
,
мұндағы: 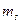 санын да спиндік кванттық сан деп атайды және ол электрон үшін келесі екі мәнді қабылдайды,
санын да спиндік кванттық сан деп атайды және ол электрон үшін келесі екі мәнді қабылдайды, 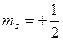 және
және 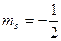 .
.
Сыртқы магнит өрісіндегі электронның спинінің өріс бағытындағы проекциясы тек дискретті екі мәндерді қабылдайды, яғни
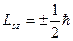 .
.
Соныменен спиндік квант сан 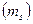 электронның сыртқы магнит өрісінің бағытындағы спиннің проекциясын анықтайды.
электронның сыртқы магнит өрісінің бағытындағы спиннің проекциясын анықтайды.
31.8.Паули принципі
Төрт кванттық санның (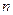 -бас кванттық сан,
-бас кванттық сан, 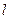 -орбитальдық кванттық сан,
-орбитальдық кванттық сан, 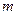 - магниттік квант сан,
- магниттік квант сан, 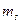 - спиндік квант сан) бірдей мәнімен анықталатын атомның стационар күйінде екі электрон бола алмайды.
- спиндік квант сан) бірдей мәнімен анықталатын атомның стационар күйінде екі электрон бола алмайды.
Атомның бірдей станционар күйлерде екі электрон болмайды.
Атомдағы электрондар үшін Паули принципін келесі түрде жазуға болады:
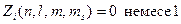 ,
,
мұндағы: 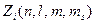 -
- 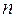 -бас кванттық сан,
-бас кванттық сан, 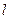 -орбитальдық кванттық сан,
-орбитальдық кванттық сан, 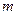 - магниттік квант сан,
- магниттік квант сан, 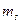 - спиндік квант сандармен анықталатын күйлердегі электрондар саны. Паули принципін пайдалана отырып
- спиндік квант сандармен анықталатын күйлердегі электрондар саны. Паули принципін пайдалана отырып 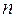 -бас кванттық санның мәнімен анықталатын күйлердегі электрондардың мүмкін болатын
-бас кванттық санның мәнімен анықталатын күйлердегі электрондардың мүмкін болатын 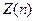 ең үлкен санын анықтауға болады, яғни ол
ең үлкен санын анықтауға болады, яғни ол 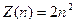 -гетең болады.
-гетең болады.
§32.Кванттық статистика негіздері
Статистикалық физикада микробөлшектердің өте үлкен санынан тұратын жүйенің қасиеттері зертттеледі. Микробөлшектің осы жүйедегі шарттарына байланысты не классикалық және кванттық механиканың заңдылықтарын пайдаланады. Микробөлшектер өзі сияқты бөлшектер жүйесіне түскенде оны басқа бөлшектерден айыру мүмкін болмайды. Бұл принцип ұқсастық принципі деп аталады.
Жүйедегі микробөлшектер екіге бөлінеді:
1. фермиондар
2. бозондар
Спиндері жартылай бүтін микробөлшектерді фермиондар деп атайды. Мысалы: фермиондарға электрон, протон, нейтрон және т.б. бөлшектер жатады.
Спиндері бүтін болатын микробөлшектерді бозондар деп атайды.
Мысалы: бозондарға фотон, пион және т.б. бөлшектер жатады. Нуклондар cаны тақ болатын ядролар фермиондар, ал жұп болатын ядролар бозондарға жатады.
32.1.Антисимметриялы және симметриялы толқындық функциялар
Мысалы: екі микробөлшектен тұратын жүйені қарастырайық.
Ұқсастық принципін ескерсек, осы екі микробөлшектердің орны ауыстырғанда жүйенің қасиеттері өзгермейді:
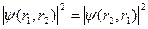
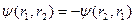 -шартын қанағаттандыратын толқындық функция антисимметриялы деп аталады.
-шартын қанағаттандыратын толқындық функция антисимметриялы деп аталады.
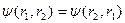 -шартын қанағаттандыратын толқындық функция симметриялы деп аталады.
-шартын қанағаттандыратын толқындық функция симметриялы деп аталады.
Антисимметриялы толқындық функциялар фермиондардың күйін сипаттайды. Ал симметриялы толқындық функциялар бозондардың күйін сипаттайды. Антисимметриялы толқындық функциямен сипатталатын екі микробөлшектің бір күйде болу ықтималдығы нольге тең.
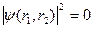 .
.
Бір мезгілде бір энергиялық күйде екі фермион болмайды.
Бірдей N микробөлшектері бар және G энергиялық күйі бар жүйе қарастырылады. Микробөлшектің белгілі бір күйде болу мүмкіндігі осы бөлшектер санының күйлер санына қатынасымен анықталады. Келесі шартпен анықталатын жүйені 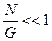 азғындалмаған жүйе деп атайды.
азғындалмаған жүйе деп атайды.
Азғындалмаған жүйеде микробөлшектің ара-қашықтығы олардың де Бройль толқын ұзындығынан көп үлкен болады (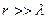 ).
).
Келесі шартпен анықталатын жүйені 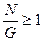 азғындалған жүйе деп атайды.
азғындалған жүйе деп атайды.
Азғындалған жүйеде микробөлшектің ара-қашықтығы олардың де Бройль толқын ұзындығынан үлкен болмайды (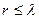 ).
).
Жүйелердегі шарттарға байланысты статистикалық физика классикалық және кванттық болып екіге бөлінеді. Азғындалмаған жүйелерді зерттейтін статистикалық физика классикалық физика деп аталады. (мысалы, Больцман, Максвелл таралулары). Кванттық статистика азғындалған жүйелердің қасиеттерін зерттейді. Кванттық статистиканың негізгі есебі микробөлшектің энергия, испульс немесе координаттар бойынша таралуын анықтау. Кванттық статистика екіге бөлінеді:
1. Фермиондардан тұратын жүйені зерттейтін кванттық статистика Ферми-Дирак статистикасы деп аталады.
2. Бозондардан тұратын жүйені зерттейтін кванттық статистика Бозе-Эйнштейн статистикасы деп аталады.
Микробөлшектер жүйесінің күйін сипаттау үшін 6 өлшемді кеңістік - фазалық кеңістік енгізіледі. 6 өлшемнің алғашқы үшеуі – x, y, z координаталар, келесі үшеуі – импульстердің проекциялары болып табылады.
Микробөлшектерге бос кеңістікте осы шамалармен анықталатын фазалық нүкте сәйкес келеді. Гейзенбергтің анықтамаушылық принциптерін ескерсек микробөлшекке фазалық кеңістікте нүкте емес ұяшық сәйкес келеді деп есептелінеді.
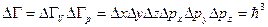
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 13498; Нарушение авторских прав?; Мы поможем в написании вашей работы!