Плоскостей

Главные направления двух аффинно-соответственных

2.3.1 Построение главных направлений

В соответствии с материалом этого раздела известно, что угол, образованный между двумя прямыми, не является инвариантом аффинного соответствия, поэтому двум перпендикулярным прямым одной плоскости могут соответствовать не перпендикулярные прямые второй плоскости.

Глубже исследуем этот вопрос для случая перспективно-аффинного соответствия, которое задано осью родства 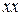и парой соответственных точек 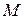и .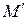

Задача сводится к следующему: требуется построить через точку 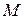пару взаимно перпендикулярных прямых 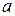и 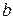так, чтобы им соответствовали также взаимно-перпендикулярные прямые 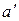и 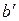, проходящие через точку (рисунок 2.19).

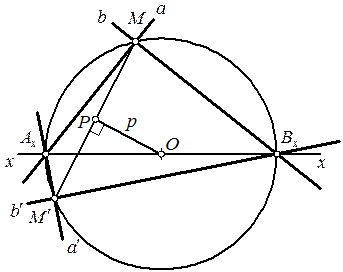
Рисунок 2.19 – Построение главных направлений

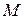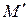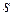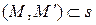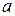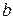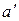Будем исходить из того, что точки и принадлежат окружности , т.е. , а прямые , и и 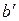, опираются на ее диаметр 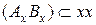. Для этого отрезок 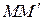делим пополам точкой 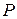, из которой проводим перпендикуляр 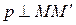; 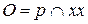– центр окружности 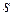, . Тогда, , .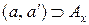

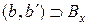Отметим, что любая пара прямых, параллельных 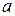и 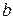имеет так же пару соответственные прямых, параллельных 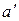и 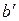(в силу инварианта параллельности).

Таким образом, найденные взаимно перпендикулярные направления называются в главными направлениями.

2.3.2 Главные направления в произвольном аффинном преобразовании

Как было отмечено в п. 2.2.3 имеет место аффинное преобразование 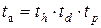. Тогда, в соответствии с рисунком 2.16, можно утверждать, что на плоскостях 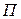и 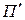существует по одной паре главных направлений, соответствующих в преобразовании 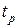, т.е это прямые 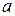, 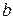и , .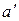

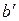Движение 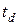сохраняет перпендикулярность пар соответственных главных направлений. Преобразование гомотетии 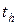переводит плоскость 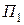в 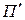, причем прямые 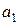, 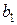перейдут в прямые 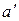, 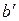. Так как при гомотетии величины углов не изменяются, то .

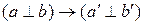Таким образом, аффинное преобразование переводит взаимно перпендикулярные прямые 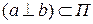в соответственные взаимно перпендикулярные прямые 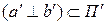. Следовательно, в произвольном аффинном соответствии двух плоскостей всегда имеются две соответственные пары главных направлений (рисунок 2.20).

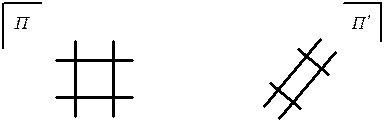
Рисунок 2.20 – Главные направления в аффинном преобразовании

Поэтому аффинное преобразование можно рассматривать как операцию растяжения или сжатия плоскости различного по двум перпендикулярным направлениям.

Дата добавления: 2014-12-27