Волгодонск

ЛЕКЦИЯ №2

« ФОРМУЛА ТЕЙЛОРА »

Формулы Тейлора и Маклорена.

Пусть функция 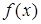n раз дифференцируема в окрестности точки x₀.Найдем многочлен 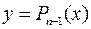степени не выше n-1, такой что

, ,,…, .

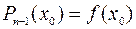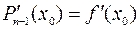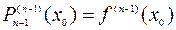Такой многочлен в некотором смысле «близок» к функции .

Будем искать этот многочлен в форме многочлена, разложенного по степеням 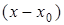, с неопределенными коэффициентами:

.

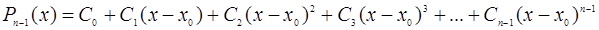Неопределенные коэффициенты 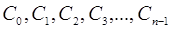определим так, чтобы выполнялись перечисленные выше условия.

Найдем производные от :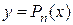

;

;…

.

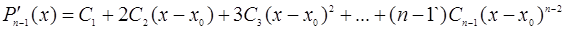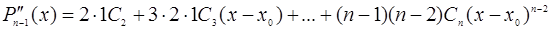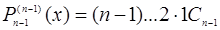Подставляя 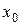вместо 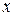, находим:

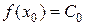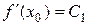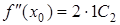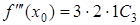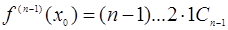, , , , …, . Отсюда

Þ , , , ,…, .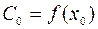

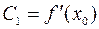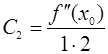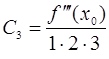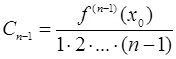Искомый многочлен будет иметь вид:

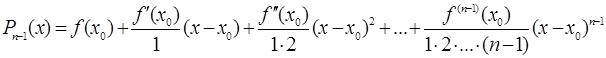, или

.

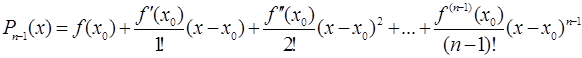Этот многочлен мы будем называть многочленом Тейлора.

Оказывается, что справедлива следующая теорема:

Теорема. Пусть функция 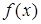n раз дифференцируема в окрестности точки x₀. Тогда в этой окрестности для функции справедлива следующая формула Тейлора:

+

+.

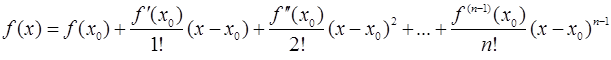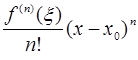Здесь 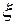некоторая точка, заключенная между 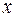и 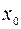(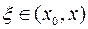), зависящая от 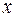, а 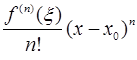= 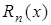- остаточный член в форме Лагранжа.

Доказательство: Обозначим через 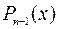многочлен

.

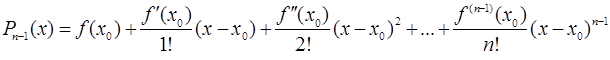Ясно, что для каждого выбранного существует такое число , для которого будет выполняться равенство:

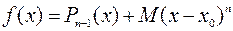. (1)

Покажем, что это число 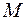при уже выбранном 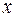будет равно 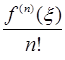при некотором 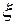из промежутка .

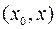Определим функцию

.

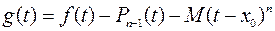Ясно, что

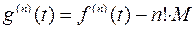
Следовательно, доказательство мы закончим, если покажем, что в некоторой точке 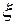(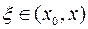) будет выполняться равенство: .

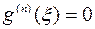Непосредственными вычислениями проверяется (см. многочлен Тейлора!), что для всех выполняются равенства:

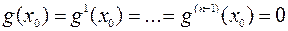(2)

Число 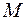выбрано таким образом, чтобы выполнялось равенство (1) и, следовательно, 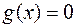. Таким образом, для функции 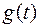на промежутке

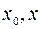[] выполняются все условия теоремы Ролля. Следовательно, на интервале (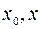) существует такая точка 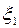, производная функции 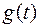, в которой равна нулю, то есть 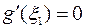. Но тогда с учетом (2) теорему Ролля можно применить к функции 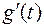на промежутке [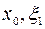] и так далее. Применяя, в конце концов, теорему Ролля к функции 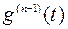на соответствующем промежутке, получим точку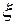, для которой будет справедливо равенство .

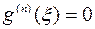Утверждение доказано.

Если x₀=0, то формула Тейлора превращается в формулу Маклорена:

+

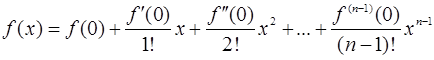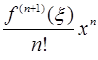
Заметим, что числа n могут выбираться различными, в зависимости и от наличия у функции производных соответствующего порядка, и от необходимой точности расчетов. Например, формула Тейлора для n=4 будет иметь вид:

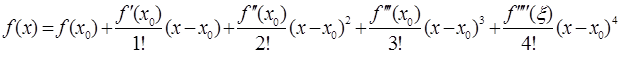
Разложение некоторых элементарных функций по формуле Маклорена.

1. .

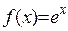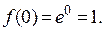
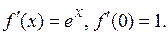
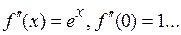
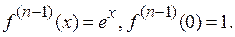
Þ ,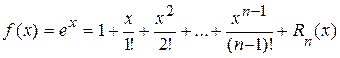

где .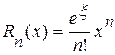

2. .

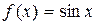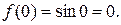
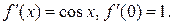
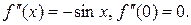
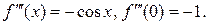
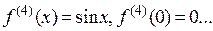
Þ ,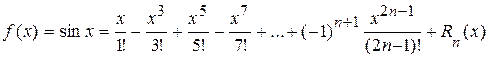

где .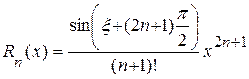

3. .

,…

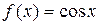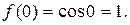
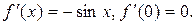
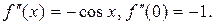
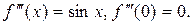
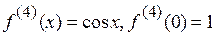Þ ,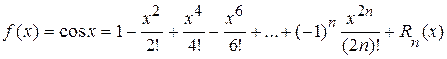

где .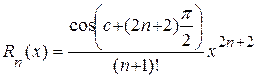

Пример:

Разложить функцию 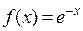по формуле Маклорена, взяв 4 слагаемых.

Воспользуемся формулой Маклорена для функции 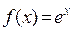, заменив x на

(-x):

.

.

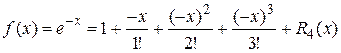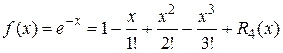Приложения формул Тейлора и Маклорена.

Формулы Тейлора и Маклорена имеют широчайшее применение, как для приближенного вычисления значений целого ряда табулированных функций таких, например, как 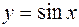, ,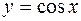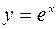и др., так и для замены сложных функций при решении практических задач многочленами.

В качестве примера приложения формулы Маклорена, определим количество членов в разложении функции 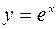по указанной формуле для вычисления ее значения с точностью до 0.001 при любом x из промежутка

[-1,1].

Поскольку 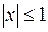, то в остаточном члене 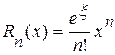величина 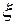удовлетворяет неравенству: 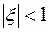. Следовательно,

.

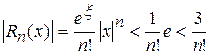Очевидно, что если мы заменим на промежутке [-1,1] функцию 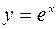соответствующим многочленом Тейлора, то значения этого многочлена на указанном промежутке будут отличаться от соответствующих значений функции на величину меньшую, чем 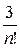. Выбирая n из условия 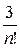<0.001, мы получим, что 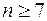, поскольку ().

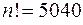Отметим, что формул Тейлора может использоваться и при вычислении пределов.

Вопросы для самоконтроля.

1. Написать формулы Тейлора и Маклорена для случаев n=2, n=3 и n=5.

Задачи для самоконтроля.

1. Разложить по формуле Тейлора функцию 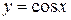в точке 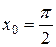для случая n=4.

2. Разложить по степеням 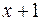многочлен .

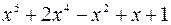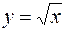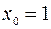3. Написать формулу Тейлора для функции при и .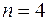

Решение типовых задач.

Задача 1. Воспользовавшись формулой Тейлора, разложить функцию 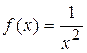по степеням бинома до четвертой степени включительно (остаточный член должен иметь сомножитель 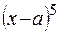) и вычислить приближенное значение функции в точке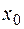, отбросив остаточный член.

(; ).

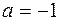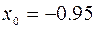Решение: Найдем значение функции 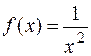и ее производных до четвертого порядка включительно в точке .

; ; ;

; ;

; .

; .

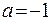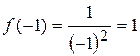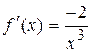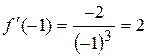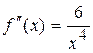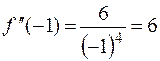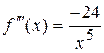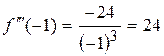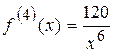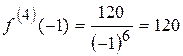Для того чтобы записать остаточный член формулы Тейлора, необходимо определить пятую производную функции 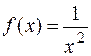в точке :

; .

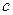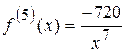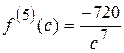Тогда

.

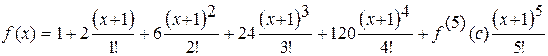Дата добавления: 2014-01-04