Третий шаг

Теперь необходимо понять, какая простая переменная первой обратится в ноль по мере увеличения входящей переменной. Для этого достаточно рассмотреть систему:

При фиксированных значениях непростых переменных система однозначно разрешима относительно простых, поэтому мы можем определить, какая из простых переменных первой достигнет нуля при увеличении входящей. Эту переменную назовем выходящей. Это будет означать, что мы натолкнулись на новую вершину. Теперь входящую и выходящую переменную поменяем местами — входящая «войдёт» в простую, а выходящая из них «выйдет» в непростые. Теперь перепишем матрицу B и вектор c_B в соответствии с новыми наборами простых и непростых переменных, после чего вернёмся ко второму шагу. x''

Поскольку число вершин конечно, то алгоритм однажды закончится. Найденная вершина будет являться оптимальным решением.

[править]Двухфазный симплекс-метод

[править]Причины использования

Если в условии задачи линейного программирования не все ограничения представлены неравенствами типа «≤», то далеко не всегда нулевой вектор будет допустимым решением. Однако каждая итерация симплекс-метода является переходом от одной вершины к другой, и если неизвестно ни одной вершины, алгоритм вообще не может быть начат.

Процесс нахождения исходной вершины не сильно отличается от однофазного симплекс-метода, однако может в итоге оказаться сложнее, чем дальнейшая оптимизация.

[править]Модификация ограничений

Все ограничения задачи модифицируются согласно следующим правилам:

· ограничения типа «≤» переводятся на равенства созданием дополнительной переменной с коэффициентом «+1». Эта модификация проводится и в однофазном симплекс-методе, дополнительные переменные в дальнейшем используются как исходный базис.

· ограничения типа «≥» дополняются одной переменной с коэффициентом «−1». Поскольку такая переменная из-за отрицательного коэффициента не может быть использована в исходном базисе, необходимо создать ещё одну, вспомогательную, переменную. Вспомогательные переменные всегда создаются с коэффициентом «+1».

· ограничения типа «=» дополняются одной вспомогательной переменной.

Соответственно, будет создано некоторое количество дополнительных и вспомогательных переменных. В исходный базис выбираются дополнительные переменные с коэффициентом «+1» и все вспомогательные. Осторожно: решение, которому соответствует этот базис, не является допустимым.

[править]Различия между дополнительными и вспомогательными переменными

Несмотря на то, что и дополнительные, и вспомогательные переменные создаются искусственно и используются для создания исходного базиса, их значения в решении сильно отличаются:

· дополнительные переменные сообщают, насколько соответствующее им ограничение «недоиспользовано». Значение дополнительной переменной, равное нулю, соответствует равенству значений правых и левых частей ограничения.

· вспомогательные переменные сообщают, насколько данное условие далеко от допустимого (относительно конкретного ограничения). Если значение вспомогательной переменной больше нуля, то данное решение не выполняет определённое ограничение, а значит не является допустимым.

То есть ненулевое значение дополнительной переменной может (но не должно) сигнализировать о неоптимальности решения. Ненулевое значение вспомогательной переменной сигнализирует о недопустимости решения.

[править]Фазы решения

После того, как было модифицировано условие, создаётся вспомогательная целевая функция. Если вспомогательные переменные были обозначены, как y_i, i∈{1,.., k}, то вспомогательную функцию определим, как

.

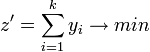После этого проводится обыкновенный симплекс-метод относительно вспомогательной целевой функции. Поскольку все вспомогательные переменные увеличивают значение 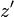, в ходе алгоритма они будут поочерёдно выводится из базиса, при этом после каждого перехода новое решение будет всё ближе к множеству допустимых решений.

Когда будет найдено оптимальное значение вспомогательной целевой функции, могут возникнуть две ситуации:

· оптимальное значение 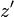больше нуля. Это значит, что как минимум одна из вспомогательных переменных осталась в базисе. В таком случае можно сделать вывод, что допустимых решений данной задачи линейного программирования не существует.

· оптимальное значение 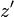равно нулю. Это означает, что все вспомогательные переменные были выведены из базиса, и текущее решение является допустимым.

Во втором случае мы имеем допустимый базис, или, иначе говоря, исходное допустимое решение. Можно проводить дальнейшую оптимизацию с учётом исходной целевой функции, при этом уже не обращая внимания на вспомогательные переменные. Это и является второй фазой решения.

[править]Модифицированный симплекс-метод

В модифицированном методе матрица

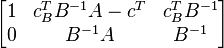
не пересчитывается, хранится и пересчитывается только матрица 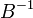. В остальном алгоритм похож на вышеописанный.

1. Вычисляем двойственные переменные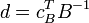

2. Проверка оптимальности. 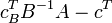преобразуется в .

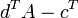Проверка заключается в вычислении 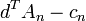для всех столбцов 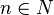. Столбец со значением < 0 можно вводить в базис.

Часто выбирают минимальное значение, но для этого нужно перебрать все столбцы.

Чаще выбирают значение, меньшее некоторого заданного значения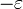

Если такого столбца не обнаружится, за принимается максимальное найденное абсолютное значение и соответствующий столбец 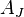вводится в базис.

3. Определение выводимого.

Пусть 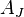- вводимый столбец, соответствующий переменной 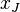Базиный план - это решение системы 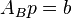Увеличиваем .

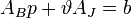Умножим слева на 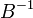, т.е. .

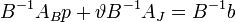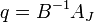Здесь - базисный план, - разложение вводимого столбца по базису.

Находим максимальное значение 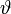, при котором все значения не отрицательны. Если 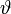может быть взято как угодно велико, решение не ограничено. В противном случае один из элементов выйдет на нулевое значение. Выводим соответствующий столбец из базиса.

4. Пересчет опорного(базисного) плана.

Вычисляем новый опорный план по уже приведенной формуле 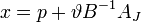с найденным значением .

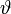5. Пересчитываем обратную к базисной .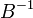

Пусть 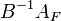- выводимый столбец.

Матрица B представима в виде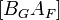

где 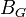- базисная матрица без выводимого столбца.

После замены столбца базисная матрица будет иметь вид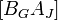

Нам нужно найти матрицу 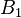, такую что

=> => =>

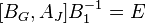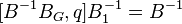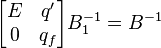
Откуда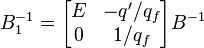

Замечание.

При пересчете матрицы 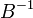накапливаются ошибки округления. Во избежание получения больших ошибок время от времени матрица пересчитывается полностью. Этот процесс называется "повторением".

[править]Мультипликативный вариант симплекс-метода

В мультипликативном варианте матрица 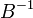не хранится, хранятся лишь множители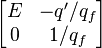

При решении экономических задач часто матрица ограничений разреженная, в таком случае мультипликативный вариант получает дополнительные преимущества - можно хранить мультипликаторы в сжатом виде (не хранить нули).

[править]Другие варианты симплекс-метода

Во избежание накопления ошибок округления может использоваться LU-разложение матрицы.

При подавляющем числе ограничений типа "неравенство" может быть использован метод переменного базиса.

Метод основан на том, что базисная матрица может быть представлена в виде

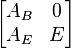
Обратная к ней имеет вид

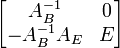
При относительно небольших размерах матрицы 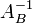остальная часть матрицы может не храниться.

Таким подходом удается решить задачи с десятками миллионов строк ограничений (например, из теории игр).

[править]Двойственный симплекс-метод

Для реализации двойственного метода необходимо перейти от задачи на минимум к задаче на максимум (или наоборот) путем транспонирования матрицы коэффициентов. При переходе от задачи на минимум целевая функция примет вид:

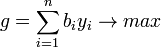
при ограничениях

.

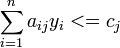Теорема двойственности. Если из пары двойственных задач одна обладает оптимальным планом, то и другая имеет решение, причем экстремальные значения линейных функций этих задач равны.

Если линейная функция одной из задач не ограничена, то другая не имеет решения.

[править]Вычислительная эффективность

Симплекс-метод удивительно эффективен на практике, но в 1972 Кли и Минти ^[1] привели пример, в котором симплекс-метод перебирал все вершины симплекса, что показывает экспоненциальную сходимость метода в худшем случае. С тех пор для каждого варианта метода был найден пример, на котором метод вел себя исключительно плохо.

Наблюдения и анализ эффективности метода в практических приложениях привело к развитию других способов измерения эффективности.

Симплекс-метод имеет среднюю полиномиальную сходимость при широком выборе распределения значений в случайных матрицах.^[2][3]

Вычислительная эффективность оценивается обычно при помощи двух параметров:

1) Числа итераций, необходимого для получения решения;

2) Затрат машинного времени.

В результате численных экспериментов получены результаты:

1) Число итераций при решении задач линейного программирования в стандартной форме с 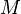ограничениями и 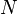переменными заключено между 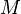и 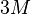. Среднее число итераций 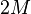. Верхняя граница числа итераций равна .

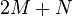2) Требуемое машинное время пропорционально .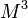

Число ограничений больше влияет на вычислительную эффективность, чем число переменных, поэтому при формулировке задач линейного программирования нужно стремиться к уменьшению числа ограничений пусть даже путём роста числа переменных.

37. Постановка задачи сегментации изображений. Пороговая сегментация.

http://cgm.computergraphics.ru/content/view/147

http://makseq.com/materials/lib/Articles-Books/Speech%20Recognition/%D0%A2%D0%B5%D0%BA%D1%81%D1%82%D1%83%D1%80%D0%BD%D0%B0%D1%8F%20%D1%81%D0%B5%D0%B3%D0%BC%D0%B5%D0%BD%D1%82%D0%B0%D1%86%D0%B8%D1%8F%20%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B9%20%D0%BD%D0%B0%20%D0%BE%D1%81%D0%BD%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B8%20%D0%BC%D0%B0%D1%80%D0%BA%D0%BE%D0%B2%D1%81%D0%BA%D0%B8%D1%85.pdf

http://habrahabr.ru/post/114153/

Дата добавления: 2014-01-04