Интерференция волн

В соответствии с определением предыдущего параграфа мы говорим об интерференции волн, когда при их совместном действии не происходит суммирования интенсивностей. Условием интерференции волн одной и той же частоты является их когерентность, т. е. сохранение неизменной разности фаз за время, достаточное для наблюдения. В частности, монохроматические волны, т. е. волны, порождаемые гармоническими колебаниями, когерентны и могут интерферировать (если, конечно, они имеют одинаковый период). Способность когерентных волн к интерференции означает, что в любой точке, которой достигнут эти волны, имеют место когерентные колебания, которые будут интерферировать. Мы будем для простоты предполагать, что обе волны одинаково линейно поляризованы. Результат интерференции определяется разностью фаз интерферирующих поли в месте наблюдения, а эта последняя зависит от начальной разности фаз волн, а также от разности расстояний, отделяющих точку наблюдения от источников каждой из волн.

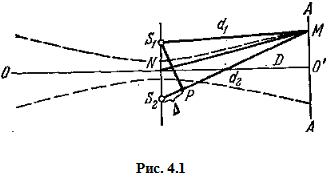
Пусть две когерентные волны исходят из источников S₁ и S ₂ (рис. 4.1), колебания в них направлены перпендикулярно к плоскости чертежа, и наблюдение производится в точке М. Допуская для простоты расчета, что в ней обе волны имеют одинаковые амплитуды, найдем, что колебания в М, вызываемые первой и второй волнами, выразятся в виде

s₁=a cos 2 π (t/T – d₁/ λ),

s₂=a cos [2 π (t/T – d₂/ λ) – φ ],

где d₁=S₁M и d₂=S₂M, λ – длина волны, а φ – начальная разность фаз.

Складываясь в точке М, колебания дадут

s=s₁+s₂=2a cos(π (d₂ – d₁)/ λ +1/2φ)cos[2 π (t/T – (d₂ + d₁)/2 λ) – 1/2φ ]

Таким образом, колебание в точке М имеет амплитуду, равную 2a cos(π (d₂ – d₁)/ λ +1/2φ), и интенсивность, пропорциональную

4a² cos² (π (d₂ – d₁)/ λ +1/2φ)

Для когерентных волн φ постоянна, и следовательно, различие интенсивности света в разных точках зависит только от различия разностей расстояний d₁ и d₂. Благодаря этой разности расстояний, или, как принято говорить, разности хода двух волн, колебания, вызванные этими волнами в точке их встречи, будут обладать разностью фаз даже в том случае, когда начальные фазы обеих волн были одинаковы. Разность фаз ψ, возникшая вследствие разности хода волн, равна

ψ =2 π (d₂ – d₁)/ λ

Выразим разность хода через длину волны Δ = d₂ – d₁ = т λ, Где т - любое число (целое или дробное). Соответствующая разность фаз ψ =2 πm. Если начальные фазы одинаковы (φ = 0), то интенсивность двух интерферирующих волн с одинаковыми амплитудами запишется в виде

I~A²=4a² cos² (π (d₂ – d₁)/ λ)=4 a² cos² тπ

Целым значениям т соответствуют различие по фазе на 2 тπ и интенсивность, пропорциональная 4 а ². При т полуцелом фазы складывающихся колебаний противоположны и интенсивность равна нулю. В общем случае т — дробное число. При неравных амплитудах интенсивность выражается соотношением

I~A² = a₁² + a₂² + 2a₁a₂ cos2 πm = (a₁ – a₂)² +4 a₁a₂ cos² тπ

При целом т имеем максимумы A² = (а₁ +а₂)², при полуцелом т минимумы A² = (а₁ - а₂)².

Таким образом, геометрическое место точек пространства, характеризующихся одинаковыми амплитудами (и интенсивностями), удовлетворяет условию (d₂ – d₁)/ λ = const, т. е. представляет собой поверхность гиперболоида вращения с осью S₁S_2, фокусами которого служат точки S₁ и S₂ (на рис. 4.1 сечение одного из таких гиперболоидов плоскостью чертежа изображено пунктиром). В частности, средняя плоскость, показанная на чертеже линией 00 ', соответствует плоскости максимальной интенсивности.

Описанное распределение интенсивностей представляет собой интерференционную картину, соответствующую интерференции двух когерентных волн с начальной разностью фаз, равной нулю. Если бы начальная разность фаз отличалась от нуля, то мы имели бы такую же картину, в которой, однако, темные и светлые полосы принимают некое промежуточное положение, зависящее от φ. Действительно, в этом общем случае условие, например, максимума интенсивности и интерференционной картине имеет вид

(d₁ – d₂)/ λ + φ/2π = т

Следовательно, отличие φ от нуля эквивалентно тому, что (d₁ – d₂)/ λ не равно целому числу, как было бы при φ = 0.

В случае некогерентных волн каждому значению φ будет соответствовать своя интерференционная картина, которая с течением времени будет сменяться другой. Если их смена происходит достаточно быстро, то мы не в состоянии наблюдать эти мгновенные интерференционные картины и воспринимаем некоторое среднее состояние, которое соответствует монотонному распределению интенсивности.

Как видно из рассмотренных примеров суперпозиции волн с равными и неравными амплитудами, соотношение между их амплитудами существенно сказывается на качестве интерференционной картины. В первом случае максимумы освещенности в интерференционной картине чередуются с областями, в которых освещенность падает до нуля, но втором случае интерференционная картина накладывается на равномерно освещенный фон. Его освещенность пропорциональна величине (а₁ - а₂)².

Возможность наблюдения чередующегося распределения светлых и темных полос в интерференционном поле существенно зависит от освещенности этого фона. Поэтому для оценки видимости, или контрастности, интерференционной картины в некоторой точке интерференционного поля Майкельсон ввел параметр видимости V, определяемый следующим образом:

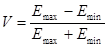
где. Е _max и Е _min — максимальная и минимальная освещенности интерференционных полос вблизи выбранной точки поля. Параметр V может изменяться в пределах от 1 до 0. Первое его значение соответствует наиболее контрастной интерференционной картине, второе — полному ее исчезновению.

Дата добавления: 2014-01-05