Методи оптимізації

В задачах оптимізації автоматичних систем керування найбільше застосування знайшли:

- принцип максимуму Л.С. Понтрягіна;

- метод динамічного програмування Р.Беллмана.

Принцип максимуму Л.С. Понтрягіна заснований на класичному варіаційному численні і є його узагальненням та випадки, коли оптимальні керування обмежені і становлять кусково-безперервні функції з точками розриву першого роду, кількість яких невідома.

Принцип максимуму є необхідною і достатньою умовою оптимальності процесу керування для лінійних об’єктів, а для нелінійних об’єктів-лише необхідним. За принципом максимуму визначається для нелінійних об’єктів не оптимальне керування, а звужена група допустимих керувань.Тоді оптимальне керування, якщо воно взагалі існує, буде належати саме до цієї групи.

Суть методу полягає в наступному. Динаміка об’єкта задається у вигляді диференціальних рівнянь:

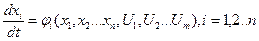(4.28)

або у векторній формі

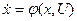(4.29)

де: 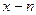- вимірний вектор координат стану; 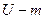- вимірний вектор керувань, який належить до замкненої множини 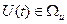, тобто для кожного 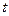керування набуває певного значення з множини.

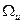Ці керування є кусково-безперервними функціями і називаються допустимими.

Задається також функіонал:

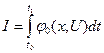(4.30)

Задача оптимізації полягає в тому, щоб серед допустимих керувань знайти таке, яке переводить об’єкт з початкового стану 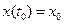в кінцевий 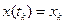, а функціонал (4.30) набуває екстремуму.

Принцип максимума передбачає використання додаткових процедур:

- вводиться додаткова штучна змінна стану :

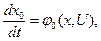(4.31)

де: 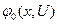відповідає підінтегральному виразу з (4.30);

- вводяться допоміжні функції 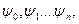,які визначається лінійними однорідними рівнянням:

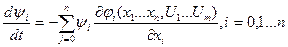(4.32)

- приєднується вираз (4.31) до системи (4.28), що утворює систему з (n+1) рівнянь

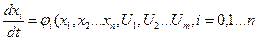(4.33)

або у векторній формі

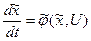(4.34)

Тут необхідно звернути увагу на такі обставини: у виразі (4.33) права частина не залежить від , а вектор 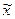та його похідна 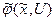є(n+1) - вимірними; критерій оптимальності стає однією з координат об’єкта керування;

- вводиться допоміжна функція 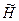(функція Гамільтона) у вигляді

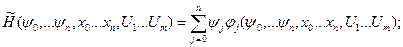(4.35)

- рівняння (4.33) та (4.32) об’єднують в одну систему (в механіці - система Гамільтона):

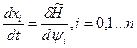(4.36)

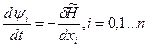(4.37)

Рівняння (4.36) - це рівняння об’єкта, а (4.37) - спряжені рівняння.

В такій постановці принцип максимуму формулюється так:

- для того, щоб керування 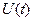і траекторія 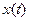, яка йому відповідає, були оптимальними, необхідно існування такої ненульової безперевної 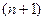- вимірної функції 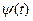, складові якої задовольняють рівняння (4.36), (4.37), щоб при будь-якому 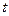у заданому інтервалі 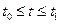величина 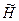як функція керувань 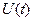у заданій зоні їх допустимих значень досягала максимуму:

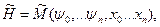(4.38)

При чому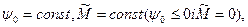

Принцип максимуму має добру геометричну інтерпретацію. Приймемо, що необхідно перевести об’єкт з початкової точки П в кінцеву К за мінімальний час (рис 4.4.)

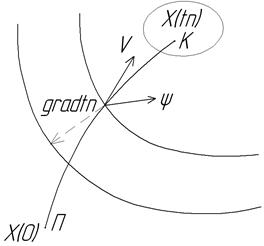
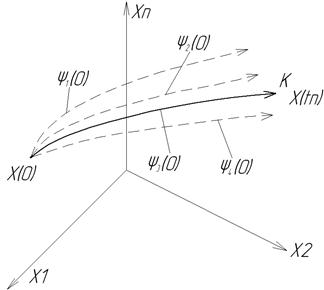
Рис 4.4. До принципу максимуму

Кожній точці фазового простору,який оточує т.К, відповідає певна оптимальна траекторія і відповідний мінімальний час переходу в цю точку. Навколо т.К можна побудувати поверхні, які будуть геометричним місцем точок з однаковим мінімальним часом переходу в т.К (рис 4.4.) - ізохрони. Оптимальна за швидкодією траекторія з точки П в точку К повинна бути максимально близькою нормалям до ізохрон, наскільки це дозволяють обмеження на кординати об’єкта і керування. Дійсно, будь-який рух вздовж ізохром збільшує час процесу, не зменшує відстань до кінцевої точки. Математично умова оптимальності траекторії означає, що скалярний добуток вектора швидкості 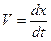та вектор, обернений до градієнта часу перехода в кінцеву точку, повинен бути максимальним (скалярний добуток двох векторів дорівнює добутку їх модулів на косинус кута між ними):

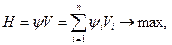(4.39)

де: 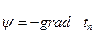, - кордината векторів

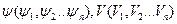
Таким чином умовою оптимальності є максимум проекції вектора 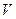на напрямок .

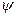Метод динамічного прграмування зручно застосовувати в задачах оптимізації багатостадійних процесів, коли оптимальну траекторію можна поділити на окремі дільниці, а стадія передбачає часовий інтервал проведення процесу. Принцип оптимальності в методі динамічного програмування формулюється так:

- будь-яка кінцева ділянка оптимальної траекторії є також оптимальною, тобто частина оптимальної траекторії від будь-якої проміжної точки до кінця буде оптимальною, якщо цю точку вважати початком траекторії. Таким чином, оптимальна стратегія не залежить від попереднього стану системи, а визначається лише її станом у даний момент;

- оптимальний розв’язок має таку властивість, що за будь-якого стану 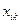, який система досягає за (і-1)-шу стадію, подальший розв’язок повинен бути оптимальним по відношенню до попереднього стану.

У фазовому просторі (рис.4.5.) показана оптимальна траєкторія 1-2 між точками П і К, і кожна її дільниця буде також оптимальною, а не 2’.

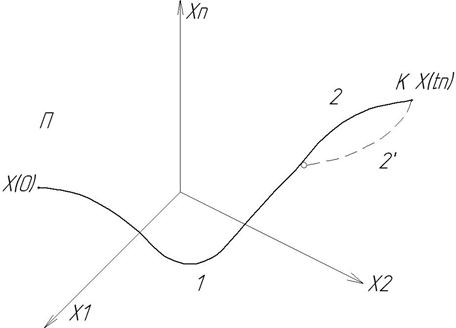
Рис 4.5. Оптимальна система руху систем

Сутність метода динамічного програмування можна пояснити на такому прикладі (рис.4.6.). Нехай об’кт необхідно перевести з точки Н в точку К за n кроків, кожний за яких, крім останнього, має 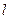варіантів і при цьому забезпечити мінімум критерія оптимальності .

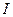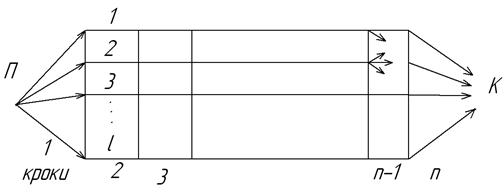
Рис. 4.6. До метода динамічного програмування

Значення цього критерія залежить від траекторії руху, і можна визначити приріст 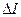на будь-якому кроці. В даному випадку значення 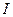є функцією 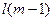змінних, а число можливих комбінацій, тобто варіантів розв’язку буде 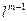. При невеликих 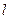та 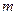оптимальний розв’язок можна знайти повним перебором варіантів, однак для реальних систем цей підхід використати неможливо: так при число варіантів буде 10⁹.

Ефективним алгоритмом є отримання розв’язку, починаючи з кінцевої точки К. Для кожної точки 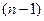-го кроку знаходять будь-яким методом, в тому числі і повним перебором оптимальну траекторію переходу в точку К. Аналогічну операцію повторяють для 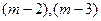і т.д кроків. Знаходження значення критерію

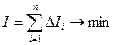(4.40)

тобто вибір з 10⁹ варіантів зводиться до послідовного вибору на кожному кроці з десяти варіантів.

Існують також алгоритми для знаходження оптимальної траекторії в прямому напрямку від т.П до т.К.

Формалізувати процедуру знаходження оптимального розв’язку за методом динамічного програмування можна так: приймається, що величина втрат 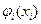визначається як мінімум за керуванням 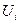суми двох доданків: втрат на і-й стадії 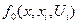і мінімальних втрат, визначених раніше 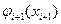за умови, що система попадає в стан . Тоді:

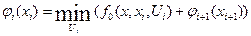(4.41)

Функцію 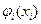називають функцією Беллмана, а рівняння (4.41)-рівнянням Беллмана. Це рекурентне співвідношення, яке зв’язує 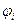та 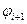. Для розв’язання цього співвідношення задаються граничні умови:

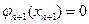, (4.42)

ому,що для переходу із стану в цей же стан не потрібно ніяких затрат. Розв’язуючи рівняння Беллмана для 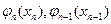і т.д., доходимо до початкової стадії, коли 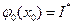, при цьому після кожної стадії визначаємо з (4.41) крім 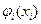також .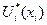

Функція Беллмана 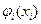дорівнює тому граничному значенню критерія оптимальності, якого можна досягти, рухаючись із стану 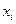як з початкового.

Для неперервних систем метод динамічного програмування в математичній постановці формулюється так. Задається нелінійне векторне диференціальне рівняння нестаціонарного об’єкта:

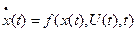(4.43)

Необхідно знайти керування 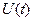, яке мінімізує функціонал:

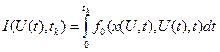(4.44)

при заданому початковому стані 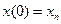, кінцевому часі 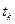, обмеженні 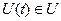та довільному кінцевому стані 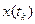. Згідно принципу оптимальності кожне поточне значення часу 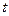на заданому інтервалі 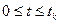може бути обрано, як початок відрахунку, і оптимальне керування, яке мінімізує функціонал (4.44) на цьому інтервалі, буде співпадати на інтервалі 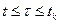з оптимальним керуванням 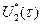,яке мінімізує функціонал:

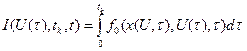(4.45)

причому мінімізоване значення 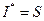функціонала (4.45) при знайденому оптимальному керуванні буде залежати лише від початкового для дільниці 2 (рис. 4.5.) стану 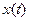і тривалості 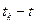процесу керування:

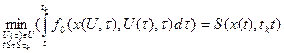(4.46)

Повна похідна інтеграла (4.43) по змінній нижній границі 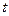буде:

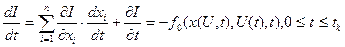(4.47)

З урахування рівнянь об’єкта (4.41):

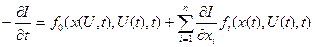(4.48)

Це рівняння справедливе для будь-якого допустимого керування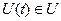, яке не виводить об’єкт на межу області 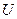. При оптимальному керуванні 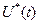це рівняння з урахуванням (4.46) набуває виду:

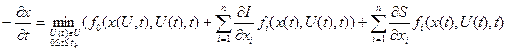(4.49)

Це рівняння Беллмана в іншій формі, яке в компактному вигляді можна записати так:

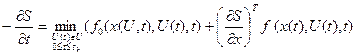(4.50)

або:

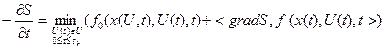(4.51)

де: 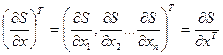вектор-стовпець, який відповідає градієнту 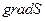склалярної функції 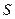векторного аргумента 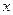, < >-позначення скалярного добутку векторів.

Рівняння Беллмана – специфічне диференціальне рівняння першого порядку в частинних похідних відносно однієї змінної 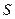. Специфічність рівняння полягає в тому, що воно включає операцію мінімізації за аргументом 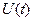і тому справедливе лише для оптимального керування .

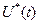Рівняння (4.49)-(4.51) виражають необхідну умову оптимальності керування і визначають порядок розв’язання задачі оптимального керування методом динамічного програмування. На першому етапі мінімізують вираз в правій частині, тобто диференціюють його за керуванням 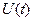і прирівнюють похідну нулю. В результаті мінімізації оптимальне керування 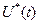виражають через функції 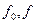та невідомі складові градієнта :

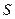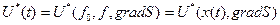(4.52)

При підстановці (4.52) в (4.51) в останньому вже не буде операції мінімізації та керування 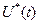,тому можна розв’язати його відносно невідомого 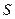при граничній умові:

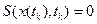(4.53)

Нарешті, отримавши функцію 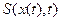та її 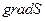за аргументом 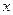та підставивши у (4.52), виражають оптимальне керування через змінні стану 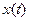. Необхідно врахувати таку обставину: якщо функції 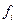та 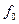не залежать явно від часу 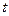, то функція 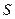також не залежить від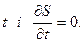

Дата добавления: 2014-01-06