Пример 1

Геометрический метод решения ЗЛП.

В случае, когда число переменных в ЗЛП равно двум, задачу можно решить геометрически. Рассмотрим примеры.

f = 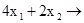max

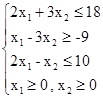
Каждое допустимое решение ЗЛП будем изображать точкой 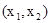координатной плоскости. Построим ОДР (рис. 2.1). Рассмотрим первое линейное ограничение 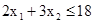. Совокупность точек плоскости, удовлетворяющих этому ограничению, представляет собой полуплоскость, ограниченную прямой 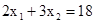. Сначала построим эту граничную прямую (ее можно построить по двум точкам: (0,6) и (9,0). Эта прямая разобьет плоскость на две полуплоскости. Чтобы решить вопрос о том, какую из этих двух полуплоскостей определяет неравенство 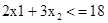, возьмем в одной из полуплоскостей какую-либо точку, не лежащую на граничной прямой, и подставим ее координаты в неравенство. Например, в качестве такой точки возьмем начало координат - точку (0,0). Поскольку 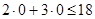, то полуплоскость, определяемая неравенством 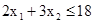, содержит точку (0,0). Аналогично находим полуплоскости, определяемые остальными ограничениями. Далее определим ОДР как общую часть полученных полуплоскостей. Получим выпуклый многоугольник

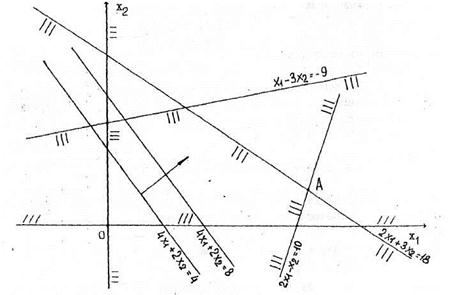
рис.2.1.

Теперь осталось определить максимум целевой функции на ОДР. Для этого построим линии уровня целевой функции. Линия уровня - это множество точек плоскости, в которых целевая функция принимает постоянное значение. Поскольку целевая функция

f =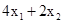,то каждая линия уровня имеет вид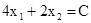. Видим, что при различных значениях параметра С получаются параллельные прямые. Построим, например, две линии уровня, положив С = 4 и С = 8. Отметим стрелкой направление, в котором перемещается линия уровня при увеличении С. Передвигая линию уровня в указанном направлении, найдем точку ОДР, в которой С имеет наибольшее значение. Это будет точка А. Она является результатом пересечения двух прямых: 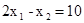и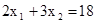

Для нахождения координат точки А решим систему

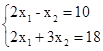
Получим оптимальное решение

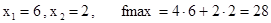
Пример 2. f =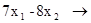min

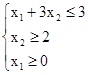
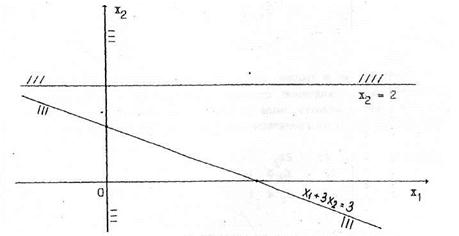
рис. 2.2.

В этом примере полуплоскости, определяемые линейными ограничениями, не имеют общих точек. Поэтому ЗЛП неразрешима из-за пустоты ОДР.

Пример 3. f =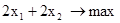

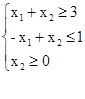
В данном примере (рис.2.3) ОДР - выпуклая неограниченная многоугольная область.

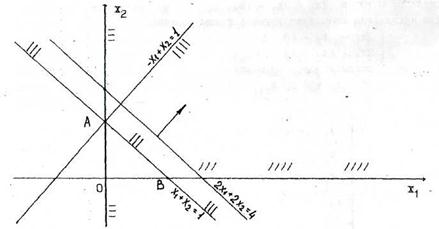
рис. 2.3.

Построим линию уровня 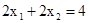. Передвигая линию уровня в направлении, указанном стрелкой, видим, что на ОДР целевая функция может принимать сколь угодно большие значения. Поэтому ЗЛП неразрешима из-за неограниченности сверху на ОДР целевой функции.

Пример 4. f =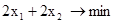

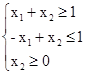
Этот пример отличается от предыдущего только тем, что целевую функцию нужно минимизировать, а не максимизировать. Линию уровня нужно перемещать в направлении, противоположном тому, которое указано на рисунке 2.3 стрелкой. Так как линия уровня параллельна прямой 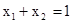, то минимальное значение на ОДР целевая функция достигает во всех точках отрезка АВ. Чтобы указать конкретное оптимальное решение задачи, нужно выписать координаты какой-либо точки этого отрезка.

Например,

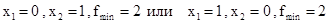
Пример 5. Решим геометрически задачу об использовании

оборудования, которая рассматривалась в параграфе 2.1. Ее математическая модель

f =

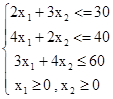
Построим ОДР (рис 2.4). Затем проведем линию уровня 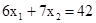. Укажем стрелкой направление, в котором перемещается линия уровня 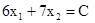с ростом C. Максимум целевой функции на ОДР достигается в точке А. Для отыскания координат точки А решим систему:

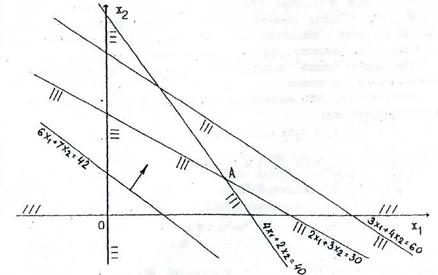
рис.2.4.

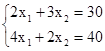
Отсюда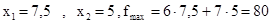

Ответ. Оптимальный план таков: изделий А нужно производить 7,5 единиц, изделий В -5 единиц; при этом прибыль будет равна 80 денежным единицам.

Геометрический метод можно использовать для решения ЗЛП с числом переменных n = 3. При большем числе переменных ЗЛП не допускает наглядного геометрического решения. Вместе с тем для произвольного числа переменных справедливы утверждения:

1) область допустимых решений представляет собой выпуклый многогранник;

2) если ЗЛП разрешима, то оптимальное решение достигается в одной из вершин выпуклого многогранника.

Дата добавления: 2014-01-07