Достаточные условия независимости функций

Условия 1 и 2, накладываемые на функции 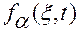в математических моделях голономных связей, проверяются легко.

Сложнее с условием 3.

Известны лишь достаточные условия независимости функций.

Они доказаны в курсе математического анализа. Приведем их применительно к функциям .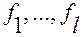

Напомним, что в нашем случае, согласно условию 2, функции 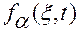заданы и дважды непрерывно дифференцируемы по совокупности переменных 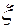и 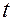в области .

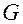Введем следующую матрицу 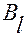, называемую матрицей Якоби:

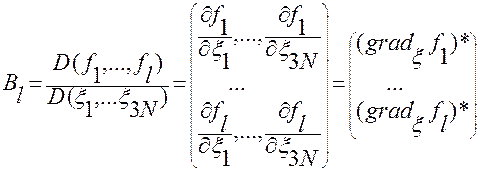. (2.4.2)

В соотношения (2.4.2) включены различные формы представления матрицы 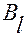, которые будут использоваться в дальнейшем.

Матрица 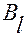имеет размерность .

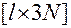В ней 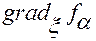обозначает вектор-столбец

,

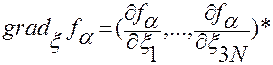где символ *(звездочка) соответствует операции транспонирования.

Иногда, в более короткой записи, матрицу 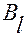будем представлять в виде

,

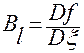где под 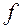и 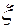понимаются векторы-столбцы

, .

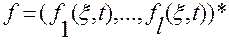Пусть 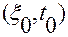— некоторая точка в области .

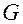Тогда справедлива следующая теорема, доказанная в курсе математического анализа.

Теорема (о независимости функций)

Если ранг матрицы Якоби равен 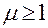, и этот ранг достигается в точке 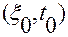, то в некоторой окрестност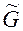и точки 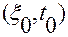будут независимы 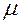функций из числа заданных 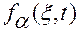, , 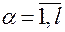а остальные от них зависят. А именно, независимыми будут те 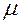функций, производные от которых входят в определитель 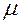- го порядка, не равный нулю в точке 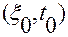и по которому определяется ранг.

Теорема дает достаточные условия независимости функций.

1.6. Формулировка третьего условия
с учетом теоремы о независимости функций

В дальнейшем будем считать, что применительно к функциям 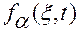, , 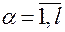выполнены условия теоремы о независимости функций во всей области 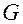, причем в этих условиях

.

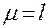Тем самым вместо условия 3, накладываемого на функции 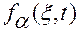, будем считать выполненным условие 3', которое формулируется следующим образом.

Условие 3': Ранг матрицы Якоби для функций , , 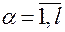вычисленной по переменным 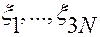, при всех значениях переменных 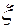, 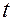из области 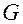задания функций 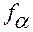, равен 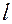, где 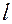— количество связей:

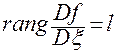. (2.4.3)

Из условия 3' следует, что уравнения геометрических связей независимы во всей области задания функций .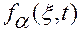

2º. Число степеней свободы положения
в голономных механических системах

Покажем, что в голономных системах можно уменьшить количество координат, с помощью которых задается любое положение механической системы.

Итак, пусть выполняются условия 1, 2, 3', указанные в п.1º для уравнений голономных связей:

1) ;

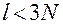2) функции 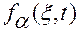— дважды непрерывно дифференцируемые по , , ;

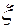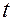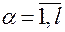3) 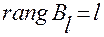, где

, , .

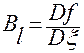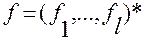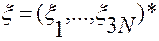Для определенности считаем, что ранг реализуется на первых 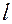столбцах матрицы Якоби .

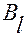В противном случае изменим нумерацию компонент вектора 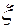и составим из них вектор .

Изменение нумерации произведем так, чтобы первые 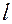компонент вектора совпали с теми компонентами вектора 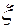, на которых реализуется ранг матрицы Якоби .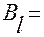

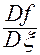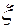Построенный таким образом вектор и его компоненты по-прежнему будем обозначать и 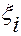, , 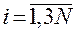соответственно.

2.1. Выделение независимых координат

Будем смотреть на уравнения связей :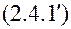

,

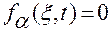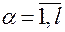
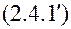
как на систему уравнений относительно переменных 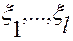, считая остальные независимые переменные 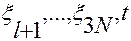параметрами.

Иначе говоря, считаем, что система уравнений

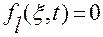,…, (2.4.4)

неявно задает 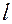функций:

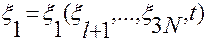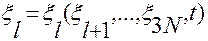,..., . (2.4.5)

Пусть в точке 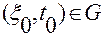выполняются равенства (2.4.4).

Поскольку для функций 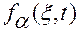, , 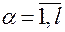справедливы условия 1,2,3', то система уравнений (2.4.4) удовлетворяет теореме о неявных функциях.

А потому, согласно утверждениям этой теоремы имеем:

1. По любой точке 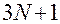-мерного пространства 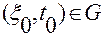, удовлетворяющей системе уравнений (2.4.4), при выполнении условия (2.4.3)

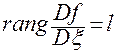(2.4.3)

можно построить окрестность 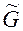точки 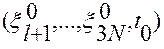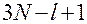- мерного пространства такую, что:

функции (2.4.5)

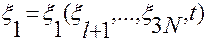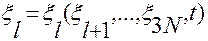,..., (2.4.5)

будут определены и непрерывно дифференцируемы в области 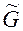столько раз, сколько раз непрерывно дифференцируемы функции .

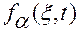2. В точке 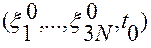выполняются соотношения

. .

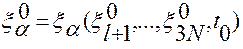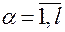3. Подстановка функций (2.4.5)

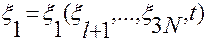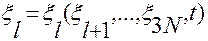,..., (2.4.5)

в уравнения (2.4.4)

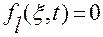,…, (2.4.4)

обращает систему уравнений связей (2.4.4) в тождества относительно переменных .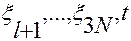

Дата добавления: 2014-01-07